* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Path integral Monte Carlo
Many-worlds interpretation wikipedia , lookup
Quantum fiction wikipedia , lookup
Copenhagen interpretation wikipedia , lookup
Molecular Hamiltonian wikipedia , lookup
Orchestrated objective reduction wikipedia , lookup
Franck–Condon principle wikipedia , lookup
Quantum dot wikipedia , lookup
Renormalization group wikipedia , lookup
Quantum field theory wikipedia , lookup
Bell's theorem wikipedia , lookup
Hydrogen atom wikipedia , lookup
Feynman diagram wikipedia , lookup
Delayed choice quantum eraser wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Renormalization wikipedia , lookup
Quantum computing wikipedia , lookup
Scalar field theory wikipedia , lookup
Quantum decoherence wikipedia , lookup
Probability amplitude wikipedia , lookup
Coherent states wikipedia , lookup
Atomic theory wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
Elementary particle wikipedia , lookup
EPR paradox wikipedia , lookup
Wave–particle duality wikipedia , lookup
Particle in a box wikipedia , lookup
Quantum entanglement wikipedia , lookup
History of quantum field theory wikipedia , lookup
Quantum machine learning wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Quantum key distribution wikipedia , lookup
Hidden variable theory wikipedia , lookup
Identical particles wikipedia , lookup
Matter wave wikipedia , lookup
Quantum teleportation wikipedia , lookup
Quantum group wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Double-slit experiment wikipedia , lookup
Density matrix wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Quantum state wikipedia , lookup
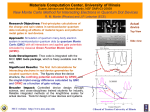
Path integral Monte Carlo Charusita Chakravarty Department of Chemistry Indian Institute of Technology Delhi Path integral Monte Carlo Methods • Finite-temperature ensembles • Metropolis Monte Carlo • Path Integral formulation of the density matrix • Discretised Path integral Methods • Fourier Path integral methods • Bosons: The superfluid transition •Fermions PARTITION FUNCTIONS AND THERMAL DENSITY MATRICES Canonical Partition Function Density Operator Expectation values Coordinate Representation of the Density Matrix Free Particle Density Matrix Semiclassical Approximation for the HighTemperature Density Matrix Path integral Representation of the Density Matrix •Multiple paths connecting initial and final points •Contributions from all possible paths are weighted by the exponential of the Euclidean action • Can be sampled by Monte Carlo methods because of the real exponential •Paths with high action will have high kinetic energy (large slopes) and/or high potential energy. •Classical limit: only the path of least action will survive. •Quantum delocalisation effects are indexed by the thermal de Broglie wavelength Partition Function: The Quantum-Classical Isomorphism System of N interacting, distinguishable quantum particles is transformed to a classical, NM-particle system at temperature e=b/M. Integral over Maxwell-Boltzmann distribution of NM particles at temperature e=b/M Potential energy at temperature e=b/M Harmonic potential with Temperature and Trotter index dependent force constant Suitable form for simulation by Metropolis Monte Carlo with increased dimensionality because of auxilliary coordinates Bead-Polymer Picture • Each quantum particle maps over to a cyclic polymer with M beads • Bead-bead interactions have different intra- and interpolymer components • Adjacent beads on the same polymer are con-nected by harmonic springs • Beads on different polymers interact with potential V(x) if they correspond to the same position in imaginary time or the same value of Trotter index • Radius of gyration of quantum polymer approximately equal to thermal de Broglie wavelength of quantum particle Sampling of Quantum Paths • Naive Sampling: •Displace beads individually •Large quantum effects imply stiff interpolymer linkages •Ergodicity of random walk difficult to ensure •Very inefficient at ensuring collective motion of polymer chain •Permutation moves will rarely be sampled • Normal mode transformation •Displace collective modes of quantum polymer •Simple to implement but will not work if quantum •effects are very large • Bisection •Very effective and will work also for bosons • Molecular dynamics •Dynamical scheme for sampling configuration space Ab initio Path Integral Simulations • Finite-temperature path integral treatment for nuclei and electronic structure methods for electrons • When do we require such methods? Light atoms: H, He, Li, B, C or when interatomic potential cannot be readily parametrised because of polarisation effects or delocalised electronic orbitals • Possible systems: Lithium clusters/Hydrogen-bonded solids e.g. ice • Coordinate basis/finite temperature for nuclei and ground Born-Oppenheimer state for electronic degrees of freedom Molecular Dynamics • By introducing NM classical particles, each of which is assigned a fictitious mass and momentum, one can write a molecular dynamics scheme will generate the same configurational averages as the MC scheme • The dynamics will be entirely fictitious and unrelated to the true quantum dynamics. • Smart computational tricks developed for classical MD can be used to generate more efficient collective motion through configuration space.e.g. multi-ple time-step MD algorithms • Quantum statistics cannot be incorporated because permutation space is discrete. • Ergodicity is problematic specially for high Trotter numbers. Require elaborate thermostatting schemes. • Efficient higher-order propagators cannot be as easily used. Marx-Parrinello Approach: Primitive approximation + normal mode transformation + molecular dynamics + density functional theory (www.cpmd.org) Lithium Clusters PIMC technique: – Discretised path integral – Takahashi-Imada approximation – Normal-mode sampling – Thermodynamic estimators Electronic structure calculations – Density functional theory. – Gradient-corrected exchange-correlation functionals. – Localised Gaussian basis set – Basis sets: 3-21G, 6-311G, 6-311G* – Double zeta plus polarization – Large uncontracted basis set. Results for Li4 and Li5+ • Quasiclassical regime- spatial correlation functions are broadened but no tunneling is seen. • HOMO and LUMO eigenvalue distributions also broadened. • Radius of gyration for Li atoms 0.15 A Weht et al, J. Chem. Phys., 1998 Identical Particle Exchange I ( x, x' ; b ) = (1 / N!) D ( x, Px' ; b ) P P Density matrix for indistinguishable particles can be written as a sum over permutations. The path integral will now contain paths which end at x’ as well as all permutational variants of x’. Classical Limit: only identity permutation will survive Bosons: sign factor will always be positive. Must sample over permutations as well as paths. Not problematic in principle Fermions: The sign problem Superfluid Transition in Liquid Helium Typical ‘‘paths’’ of six helium atoms in 2D. The filled circles are markers for the (arbitrary) beginning of the path. Paths that exit on one side of the square reenter on the other side. The paths show only the lowest 11 Fourier components. (a) shows normal 4He at 2 K (b) superfluid 4He at 0.75 K.