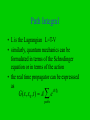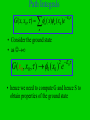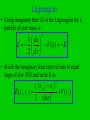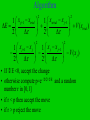Download Path Integral Quantum Monte Carlo

Path Integral Quantum
Monte Carlo
• Consider a harmonic oscillator potential
• a classical particle moves back and forth
periodically in such a potential
• x(t)= A cos(t)
• the quantum wave function can be thought
of as a fluctuation about the classical
trajectory
Feynman Path Integral
• The motion of a quantum wave function is
determined by the Schrodinger equation
• we can formulate a Huygen’s wavelet principle for
the wave function of a free particle as follows:
• each point on the wavefront emits a spherical
wavelet that propagates forward in space and time
 ( xb , tb )   dxa G ( xb , tb ; xa , ta )  ( xa , ta )
Feynman Paths
• The probability amplitude for the particle to
be at xb is the sum over all paths through
spacetime originating at xa at time ta
 ( xb , tb )   dxa G ( xb , tb ; xa , ta )  ( xa , ta )
2

i( xb  xa ) 
1
G( xb , tb ; xa , ta ) 
exp 

2 i(tb  ta )
 2(tb  ta ) 
Principal Of Least Action
• Classical mechanics can be formulated
using Newton’s equations of motion or in
terms of the principal of least action
• given two points in space-time, a classical
particle chooses the path that minimizes the
action
x ,t
S

x0 ,0
Ldt 
Fermat
Path Integral
• L is the Lagrangian L=T-V
• similarly, quantum mechanics can be
formulated in terms of the Schrodinger
equation or in terms of the action
• the real time propagator can be expresssed
as
G ( x, x0 , t )  A  e
paths
iS /
Propagator
G ( x, x0 , t )  A  e
iS /
paths
• The sum is over all paths between (x0,0) and
(x,t) and not just the path that minimizes the
classical action
• the presence of the factor i leads to
interference effects
• the propagator G(x,x0,t) is interpreted as the
probability amplitude for a particle to be at
x at time t given it was at x0 at time zero
Path Integral
 ( x, t )   G ( x, x0 , t ) ( x0 , 0)dx0
• We can express G as
G( x, x0 , t )  n ( x)n ( x0 )e
 iEnt /
n
• Using imaginary time =it/
G( x, x0 , )  n ( x)n ( x0 )e
n
 En
t 0
Path Integrals
G( x, x0 , )  n ( x)n ( x0 )e
 En
n
• Consider the ground state
• as 
G ( x0 , x0 ,  )  0 ( x0 ) e
2
 E0
• hence we need to compute G and hence S to
obtain properties of the ground state
Lagrangian
• Using imaginary time =it the Lagrangian for a
particle of unit mass is
2
1  dx 
L      V ( x)   E
2  d 
• divide the imaginary time interval into N equal
steps of size  and write E as
1 ( x j 1  x j )
E ( x j , j ) 
V (x j )
2
2 ( )
2
x ,t
S

x0 ,0
Action
Ldt 
1 ( x j 1  x j )
E ( x j , j ) 
V (x j )
2
2 ( )
2
• Where j = j and xj is the displacement at time
j
N 1
S  i  E ( x j , j )
j 0
 N 1 1 ( x j 1  x j )2

 i 
 V ( x j )
2
 j 0 2 ( )

Propagator
• The propagator can be expressed as
G ( x, x0 , t )  A  e
iS /
paths
e e
iS
 N 1 1 ( x j 1  x j )2


 

V
(
x
)
j
 j 0 2 (  )2


G ( x, x0 , N  )  A dx1...dxN 1e
 N 1 1 ( x j 1  x j ) 2

 
V ( x j ) 
2
 j 0 2 (  )


Path Integrals
G ( x, x0 , N  )  A dx1...dxN 1e
•
•
•
•
 N 1 1 ( x j 1  x j ) 2

 
V ( x j ) 
2
 j 0 2 (  )


This is a multidimensional integral
the sequence x0,x1,…,xN is a possible path
the integral is a sum over all paths
for the ground state, we want G(x0,x0,N )
and so we choose xN = x0
• we can relabel the x’s and sum j from 1 to N
Path Integral
G ( x0 , x0 , N  )  A dx1...dxN 1e
 N 1 ( x j  x j 1 )2

 
V ( x j ) 
2
 j 1 2 (  )


• We have converted a quantum mechanical
problem for a single particle into a
statistical mechanical problem for N
“atoms” on a ring connected by nearest
neighbour springs with spring constant
1/( )2
Thermodynamics
G ( x0 , x0 , N  )  A dx1...dxN 1e
 N 1 ( x j  x j 1 )2

 
V ( x j ) 
2
 j 1 2 (  )


• This expression is similar to a partition function Z in
statistical mechanics
• the probability factor e- E in statistical mechanics
is the analogue of e- E in quantum mechanics
•  =N  plays the role of inverse temperature
=1/kT
Simulation
• We can use the Metropolis algorithm to simulate the
motion of N “atoms” on a ring
• these are not real particles but are effective particles
in our analysis
• possible algorithm:
• 1. Choose N and  such that N  >>1 ( low T)
also choose ( the maximum trial change in the
displacement of an atom) and mcs (the number of
steps)
Algorithm
• 2. Choose an initial configuration for the
displacements xj which is close to the
approximate shape of the ground state
probability amplitude
• 3. Choose an atom j at random and a trial
displacement xtrial ->xj +(2r-1) 
where r is a random number on [0,1]
• 4. Compute the change E in the energy
Algorithm
1  x j 1  xtrial  1  xxtrial  x j 1 
E  
  
  V ( xtrial )
2


 2

2
2
1  x j 1  x j  1  x j  x j 1 
 
  
 V (x j )
2    2   
2
2
• If E <0, accept the change
• otherwise compute p=e-  E and a random
number r in [0,1]
• if r < p then accept the move
• if r > p reject the move
Algorithm
• 4. Update the probability density P(x). This
probability density records how often a
particular value of x is visited
Let P(x=xj) => P(x=xj)+1 where x was
position chosen in step 3 (either old or new)
• 5. Repeat steps 3 and 4 until a sufficient number
of Monte Carlo steps have been performed
qmc1
Excited States
• To get the ground state we took the limit  
• this corresponds to T=0 in the analogous statistical
mechanics problem
• for finite T, excited states also contribute to the
path integrals
• the paths through spacetime fluctuate about the
classical trajectory
• this is a consequence of the Metropolis algorithm
occasionally going up hill in its search for a new
path