* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Thesis Presentation Mr. Joshuah T. Heath Department of Physics
Coherent states wikipedia , lookup
Quantum field theory wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
Quantum entanglement wikipedia , lookup
Nuclear structure wikipedia , lookup
Bose–Einstein statistics wikipedia , lookup
Electron scattering wikipedia , lookup
Wave packet wikipedia , lookup
Quantum tomography wikipedia , lookup
Relational approach to quantum physics wikipedia , lookup
Uncertainty principle wikipedia , lookup
Density matrix wikipedia , lookup
Introduction to quantum mechanics wikipedia , lookup
Quantum tunnelling wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Compact Muon Solenoid wikipedia , lookup
History of quantum field theory wikipedia , lookup
ATLAS experiment wikipedia , lookup
Quantum vacuum thruster wikipedia , lookup
Quantum potential wikipedia , lookup
Future Circular Collider wikipedia , lookup
Ensemble interpretation wikipedia , lookup
Quantum chaos wikipedia , lookup
Double-slit experiment wikipedia , lookup
Mathematical formulation of the Standard Model wikipedia , lookup
Renormalization wikipedia , lookup
Scalar field theory wikipedia , lookup
Monte Carlo methods for electron transport wikipedia , lookup
Quantum logic wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Quantum state wikipedia , lookup
Old quantum theory wikipedia , lookup
Grand Unified Theory wikipedia , lookup
Renormalization group wikipedia , lookup
Standard Model wikipedia , lookup
Canonical quantum gravity wikipedia , lookup
Path integral formulation wikipedia , lookup
Eigenstate thermalization hypothesis wikipedia , lookup
Identical particles wikipedia , lookup
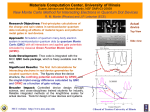
Thesis Presentation Mr. Joshuah T. Heath Department of Physics University of Vermont Adviser: Professor Adrian Del Maestro Pressure-Energy Relation in Canonical 2D Dipolar Bosons: A Path Integral Monte Carlo Study One of the simplest conceptual models in quantum statistical physics is a gas of noninteracting particles with bosonic symmetry. In the grand canonical ensemble, particle number and temperature are in equilibrium with an external reservoir and an exact analytical expression can be derived for the partition function at any density and chemical potential. In the canonical ensemble, the total number of particles, N, is fixed and an expression for the partition function can only be generated via a complicated recursion relation. In this work we apply the recursion formula to obtain the partition function, and thus all thermodynamic quantities, for up to 4 non-interacting bosons in three spatial dimensions at low temperature. Analytical results for the pressure and energy are confirmed using exact path integral quantum Monte Carlo simulations. From here, we turn on weak dipolar interactions between the particles in two spatial dimensions and illustrate how quantum Monte Carlo simulations can be used to explore the relationship between pressure and energy in a system that could be experimentally realized using ultra-cold atomic gases. Wednesday, April 29, 2015 8:00 AM Cook Science A442




![EEE 350 Random Signal Analysis (3) [F, S, SS]](http://s1.studyres.com/store/data/020200611_1-c0c63b0ea32487ef11fe760f507ca8a3-150x150.png)

![EEE 350 Random Signal Analysis (3) [F, S, SS]](http://s1.studyres.com/store/data/023352477_1-deef8e1ae340b8e5ce1a0ae7390134d0-150x150.png)


