* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download MA171 - Mohawk Valley Community College
Positional notation wikipedia , lookup
History of mathematical notation wikipedia , lookup
History of mathematics wikipedia , lookup
Infinitesimal wikipedia , lookup
Georg Cantor's first set theory article wikipedia , lookup
Ethnomathematics wikipedia , lookup
Proofs of Fermat's little theorem wikipedia , lookup
Hyperreal number wikipedia , lookup
Surreal number wikipedia , lookup
Large numbers wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
List of important publications in mathematics wikipedia , lookup
System of polynomial equations wikipedia , lookup
Foundations of mathematics wikipedia , lookup
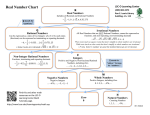
Real number wikipedia , lookup
MOHAWK VALLEY COMMUNITY COLLEGE UTICA, NEW YORK COURSE OUTLINE MA171 FOUNDATIONS OF MATHEMATICS 1 REVIEWED AND REVISED BY JULIE DEWAN – 5/03 REVISED BY JULIE DEWAN – 12/03 REVIEWED AND FOUND ACCEPTABLE BY JULIE DEWAN – 5/04 REVISED BY JULIE DEWAN – 12/04 REVISED BY JULIE DEWAN – 5/05 REVISED BY JULIE DEWAN – 5/06 REVIEWED AND REVISED BY JULIE DEWAN – 5/07 REVIEWED AND REVISED BY JULIE DEWAN – 5/08 REVIEWED AND REVISED BY JULIE DEWAN – 5/09 REVIEWED AND FOUND ACCEPTABLE BY EMILY HANTSCH – 5/10 REVIEWED AND FOUND ACCEPTABLE BY EMILY HANTSCH – 5/11 REVIEWED AND FOUND ACCEPTABLE BY ALEXANDER HAINES-STEPHAN – 5/12 REVISED FOR NEW EDITION BY ALEXANDER HAINES-STEPHAN – 1/13 REVIEWED AND FOUND ACCEPTABLE BY ALEXANDER HAINES-STEPHAN 5/13 REVIEWED AND FOUND ACCEPTABLE BY ALEXANDER HAINES-STEPHAN 5/14 REVISED FOR NEW EDITION BY ALEXANDER HAINES-STEPHAN – 5/16 COURSE OUTLINE TITLE: Foundations of Mathematics 1 CATALOG NUMBER: MA171 CREDIT HOURS: 3 LAB HOURS: 0 PREREQUISITES: An appropriate placement test result or MA 090 essential math skills or MA 096 Mathematical Literacy. CATALOG DESCRIPTION: COURSE OBJECTIVES: This is the first of a two-course sequence for students preparing to teach at the elementary school level. Topics include the study of real numbers through a development of natural numbers, whole numbers, integers, rational numbers, decimals, and irrational numbers, together with operations on them. Number theory is presented, along with a discussion of numeration systems including bases other than ten. The language and nature of reasoning, together with basic elements of set theory, are introduced. Problem-solving is emphasized. 1. To provide the student with an appreciation and understanding of the basic structure of mathematics. 2. To introduce the student to some mathematical sophistication using the axiomatic approach. 3. To provide the student who is preparing to teach at the elementary grade level with an appropriate basis for understanding the arithmetic of the real numbers. 4. To put the mathematical structures in a historical context and to introduce the student to some of the important mathematicians and their work. Topic 1. Introduction to Mathematical Reasoning The student will be introduced to different types of mathematical reasoning including inductive, deductive and intuitive. Polya’s four steps in problem solving will be introduced. Valid arguments and ways to establish the validity of an argument are introduced. Student Outcomes: The student will be able to: 1. distinguish between deductive and inductive reasoning. 2. recognize number patterns in sequences and apply formulas for arithmetic and geometric sequences. 3. apply problem solving techniques to a variety of problems. 4. determine the validity of an argument using an Euler Diagram or deductive reasoning. Topic 2 Sets and Relations: Ways of identifying sets, types of sets, operations on sets, and relations between sets will be discussed. Equivalence Relations and one-to-one correspondences will be discussed. The concept of a function will be introduced. Student Outcomes: The student will be able to: 1. 2. 3. identify the universal set, the empty set, and find the complement of a set. identify subset relations and determine the number of subsets. perform the operations of set union, intersection, set difference and the Cartesian products of two sets. 4. distinguish between finite and infinite sets. 5. find a one-to-one correspondence between two sets, if one exists, and identify equivalent sets. 6. use a Venn Diagram to illustrate relations between sets, operations on sets, and to analyze data. 7. determine if a given diagram, relation, or graph represents a function or not. 8. identify the domain and range of a function. 9. evaluate a function for a given value in the domain. 10. graph a linear function. Topic 3: The System of Whole Numbers The student will be introduced to an historical development of the whole numbers. Natural numbers and whole numbers will be introduced together with operations on them. Properties associated with these operations will also be discussed. The relation of order will be introduced. The number line will also be introduced and discussed. Student Outcomes: The student will be able to: 1. 2. 3. 4. 5. 6. 7. 8. 9. within the Hindu-Arabic System write numbers in bases other than 10. perform the four basic operations in base 10 and other bases. determine the meaning of a/0, 0/b, and 0/0. identify the properties of the operations of whole numbers. demonstrate a variety of techniques to estimate addition, subtraction, multiplication, and division of whole numbers. apply the rules for divisibility for 2, 3, 4, 5, 6, 9, and 10. recognize a prime number. find the prime factorization of a given number. find the greatest common divisor and least common multiple of a collection of numbers using the method of intersection of sets or the prime factorization method. Topic 4: The System of Integers The student will be introduced to the system of integers and the reasons for their introduction. Operations on the integers will be discussed together with the properties associated with these operations. The order relation will be discussed and the number line will be extended. As the number system is developed, a variety of topics from number theory will be explored. Student Outcomes: The student will be able to: 1. 2. 3. 4. 5. 6. perform the four basic operations on integers. find the absolute value of an integer. identify the properties of the operations of integers. find the additive inverse of an integer. order a collection of integers using the number line or other methods. evaluate expressions using the order of operations. Topic 5: Fractions and Rational Numbers The student will be introduced to the system of rational numbers and the reasons for their introduction will be discussed. Operations on the rational numbers will be discussed together with the properties associated with these operations. The order relation will be discussed and the number line will be further extended. Student Outcomes: The student will be able to: 1. 2. 3. 4. 5. 6. 7. 8. 9. identify a fraction and a rational number. determine the equality of rational numbers. simplify rational numbers. order a given collection of rational numbers. perform the four basic operations on rational numbers. find the additive and multiplicative inverses of a rational number. identify the properties of operations on rational numbers. apply the rules of exponents to rational numbers. evaluate expressions involving negative exponents. Topic 6: Decimals and Real Numbers The student will be introduced to the concept of decimals. Terminating and repeating decimals will be discussed. These topics will be used to introduce the irrational numbers as neither of these. This leads to the introduction of the real number system and the completion of the real number line. Student Outcomes: The student will be able to: 1. 2. 3. 4. 5. 6. convert between scientific and normal notation. perform the four basic operations on decimals. convert between rational and decimal numbers. order a given collection of real numbers. solve equations involving one of three terms missing, the percent, the base, or the percentage. solve problems using percents. 7. 8. 9. 10. 11. 12. identify an irrational number. classify real numbers. identify the properties of the real number system. evaluate expressions using rational exponents. determine a ratio and form a proportion. use a proportion to solve an appropriate problem. Topic 7: Algebraic Expressions and Linear Equations Algebraic expressions are defined. The basic operations of combining algebraic expressions are covered. Methods for solving linear equations in one variable are included. Student Outcomes: The student will be able to: 1. Combine and simplify algebraic expressions. 2. Determine solutions to first degree equations by applying the addition and multiplication properties of equations. 3. Translate given verbal statements into algebraic expressions. 4. Translate given verbal sentences into equations and solve the resulting equations. TEACHING GUIDE TITLE: Foundations of Mathematics 1 CATALOG NUMBER: MA171 CREDIT HOURS: 3 LAB HOURS: 0 PREREQUISITES: An appropriate placement test result or MA 090 essential math skills or MA 096 Mathematical Literacy. CATALOG DESCRIPTION: This is the first of a two-course sequence for students preparing to teach at the elementary school level. Topics include the study of real numbers through a development of natural numbers, whole numbers, integers, rational numbers, decimals, and irrational numbers, together with operations on them. Number theory is presented, along with a discussion of numeration systems including bases other than ten. The language and nature of reasoning, together with basic elements of set theory, are introduced. Problemsolving is emphasized. TEXT: A Problem Solving Approach to Mathematics for Elementary School Teachers, 12th edition, Billstein, Libeskind, Lott, Addison-Wesley Pub., 2016. NOTE: The calculator may be used on graded work in this course once the student has demonstrated to the instructor's satisfaction an understanding of the concepts that can be duplicated by the calculator. Chapter 1: An Introduction to Problem Solving 1.1 1.2 3 hours Mathematics and Problem Solving Explorations with Patterns Chapter 2: Introduction to Logic and Sets 2.1 Reasoning and Logic: An Introduction 6 hours 2.2 Describing Sets 2.3 Other Set Operations and Their Properties Chapter 3: Numeration Systems and Whole Number Operations 3.1 3.2 3.3 3.4 3.5 8 hours Numerations Systems Addition and Subtraction of Whole Numbers Multiplication and Division of Whole Numbers Algorithms for Whole-Number Addition and Subtraction Algorithms for Whole-Number Multiplication and Division Chapter 4: Number Theory 3 hours 4.1 Divisibility 4.2 Prime and Composite Numbers 4.3 Greatest Common Divisor and Least Common Multiple Chapter 5: Integers 5.1 5.2 Addition and Subtraction of Integers Multiplication and Division of Integers Chapter 6: Rational Numbers and Proportional Reasoning 6.1 6.2 6.3 6.4 7 hours Introduction to Finite Decimals Operations on Decimals Repeating Decimals Percents and Interest Chapter 8: Real Numbers and Algebraic Thinking 8.1 8.2 8.3 8.4 6 hours The Set of Rational Numbers Addition, Subtraction, and Estimation with Rational Numbers Multiplication, Division and Estimation with Rational Numbers Proportional Reasoning Chapter 7: Rational Numbers as Decimals and Percents 7.1 7.2 7.3 7.4 3 hours 6 hours Real numbers Variables Equations Functions The teaching guide allows 3 additional hours for the in-class assessment of student learning. A two-hour comprehensive final examination will also be given.