Download real number line

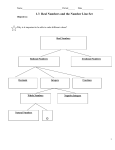
Algebra
2.1 The Real Number Line
Real Numbers
Real Number Line
Real numbers can be pictured as points on a
line called a real number line, or simply a
number line.
Positive vs Negative
Every real number is either positive or negative, or
zero. Points to the left of zero represent the negative
real numbers. Points to the right of zero represent
the positive real numbers. Zero is neither positive
nor negative.
Integers
An integer is either negative, zero, or positive
and does not contain a fraction or decimal.
Whole Numbers
Zero and the positive integers
Examples
Graph the numbers on a number line. Then write
two inequalities that compare the numbers.
1. -6 and -2
2. 2 and -3
3. 5 and 7
Note
When you work with fractions, sometimes it is easier
to first convert the fraction to a decimal.
Examples
Graph the numbers on a number line, and
then write the numbers in increasing order.
1. -3, 0, 4, -5/4, 3/2, -1
2. -3, 3, 3.2, -1/2, -8, 4.5
Algebra
2.2 Absolute Value
Opposites
Two numbers that are the same distance from
0 on a number line but on opposite sides of 0
are opposites.
Absolute Value
The absolute value of a number is its distance
from zero on a number line.
The symbol
of x.
represents the absolute value
Example
Use mental math to solve the equation
1.
=7
2.
= 5.1
3.
= (-2/9)
Velocity and Speed
Velocity indicates both speed and direction
(up is positive and down is negative). The
speed of an object is the absolute value of its
velocity.
Example
A parachutist descends at a rate of about 17
feet per second.
1. What is the parachutist’s velocity?
2. What is the parachutist’s speed?
Example
If wind resistance is ignored, an object falling
close to Earth’s surface falls at a rate of 32
ft/sec. What are the object’s velocity and
speed?
COUNTEREXAMPLE
To prove that a statement is true, you need to
show that it is true for all examples. To prove
that a statement is false, it is enough to show
that it is not true for a single example, called a
counterexample.
Examples
Determine whether the statement is true or
false. If it is false, give a counterexample.
1. The opposite of a number is always negative.
2. The absolute value of a number is never
negative.
Examples
Determine whether the statement is true or
false. If it is false, give a counterexample.
1. The expression –a is never positive.
2. The absolute value of a negative number is
always negative.