Download Title

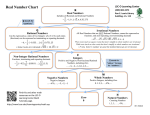
Let’s do some Further Maths

What sorts of numbers do we already know
about?
Natural
numbers:
1,2,3,4...
Integers: 0, -1,
-2, -3
Rational numbers:
½, ¼,...
Irrational numbers:
π, √2
Let’s do some Further Maths
Natural
numbers:
1,2,3,4...
Integers: 0, -1,
-2, -3
Rational numbers:
½, ¼,...
Irrational numbers:
π, √2
Complex numbers
Why would we ever need
complex numbers?

Solving quadratic equations: ax2+bx+c=0

Solving cubic equations


square roots of negative numbers appear in
intermediate steps even when the roots are real
Fundamental Theorem of Algebra- every
polynomial of degree n has n roots
We only need one new number
We define the number i = √-1 so that i2=-1
 All square roots of negative numbers can be
written using i
 √-4 = √4 x √-1 = 2i

Exercise
Write the following using i:
1. √-36
2. √-121
3. √-10
4. √-18
5. -√-75
We treat i a little like x
Exercise
Simplify:
1. 3i + 2i
2. 16i – 5i 3. (2i)(3i)
5. Copy and complete: i0 =
i1 =
i2 =
i3 =
i4 =
i5 =
i6 =
6. i12 =
7. i25 =
4. i(4i)(6i)
8. i1026 =
Complex Numbers
Multiples of i are imaginary numbers
 Real numbers can be added to imaginary
numbers to form complex numbers like 3+2i
or -1/2 -√2i
 We can add, subtract and multiply complex
numbers (dividing is a little more
complicated!)
Exercise
1. (3+2i) + (-1-4i) =
2. (2-i) – (1+5i) =

3. (2-2i)(1+3i) =
Where are complex numbers
on the number line?
Is i positive or negative?
Suppose i > 0.
 Then i2 > 0.
 In other words, -1 > 0.

So i < 0.
 Then i + (-i) < 0 +(-i).
 So –i > 0.
 And (-i)2 > 0.
 In other words, -1 > 0.

We need a 2-D number line!
C
D
F
B
A
E
Exercise
G
I
H
Name the complex
numbers
represented by each
point on the Argand
diagram.
What will squaring do to
this man?
Oops!