List of available projects - HTTrack Website Copier
... Vedic Mathematics | Upa-Sutras anurupyena ĀNURŨPYENA The upa-Sutra 'anurupyena' means 'proportionality'. This Sutra is highly useful to find products of two numbers when both of them are near the Common bases i.e powers of base 10 . It is very clear that in such cases the expected 'Simplicity ' in d ...
... Vedic Mathematics | Upa-Sutras anurupyena ĀNURŨPYENA The upa-Sutra 'anurupyena' means 'proportionality'. This Sutra is highly useful to find products of two numbers when both of them are near the Common bases i.e powers of base 10 . It is very clear that in such cases the expected 'Simplicity ' in d ...
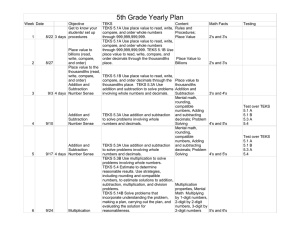
5th Grade Yearly Plan
... TEKS 5.2A Generate a fraction equivalent to a given fraction such as 1/2 and 3/6 or 4/12 and 1/3. TEKS 5.3D Identify common factors of a set of whole numbers. TEKS 5.5B Identify prime and composite numbers using concrete objects, pictorial models, and patterns in factor pairs. TEKS 5.3D Identify com ...
... TEKS 5.2A Generate a fraction equivalent to a given fraction such as 1/2 and 3/6 or 4/12 and 1/3. TEKS 5.3D Identify common factors of a set of whole numbers. TEKS 5.5B Identify prime and composite numbers using concrete objects, pictorial models, and patterns in factor pairs. TEKS 5.3D Identify com ...
B. Divisibility
... A problem in Abacus was to prove sum of divisors that every number n > 3 is the sum of two deficient numbers, or to find a number that was not. If σ(n) > 2n, then n is called abundant. If σ(n) = 2n − 1, n has been called almost perfect. Powers of 2 are almost perfect; it is not known if any other numb ...
... A problem in Abacus was to prove sum of divisors that every number n > 3 is the sum of two deficient numbers, or to find a number that was not. If σ(n) > 2n, then n is called abundant. If σ(n) = 2n − 1, n has been called almost perfect. Powers of 2 are almost perfect; it is not known if any other numb ...
Open Problems in Mathematics - School of Mathematical Sciences
... is to the pencil sharpener. 4 So you’ll understand that the distributive property has nothing to do with real estate. 3 Because solving word problems could lead to solving the world’s problems. 2 To learn that Dewey didn’t invent the decimal. 1 If you can’t count to a million, how will you know if y ...
... is to the pencil sharpener. 4 So you’ll understand that the distributive property has nothing to do with real estate. 3 Because solving word problems could lead to solving the world’s problems. 2 To learn that Dewey didn’t invent the decimal. 1 If you can’t count to a million, how will you know if y ...
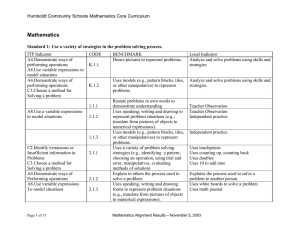
Math - Humboldt Community School District
... Using logical reasoning arguments Predict or estimate Justify answers in verbal and written form Understand that some ways of State problems in own works to increase representing a problem are more understanding helpful than others. Distinguish between pertinent and irrelevant ...
... Using logical reasoning arguments Predict or estimate Justify answers in verbal and written form Understand that some ways of State problems in own works to increase representing a problem are more understanding helpful than others. Distinguish between pertinent and irrelevant ...
Those Incredible Greeks! - The Saga of Mathematics: A Brief History
... generators p = 3 and q = 2. Using the equations for a, b and c we get a = 32 22 = 5, b = 232 = 12, and c = 32 + 22 = ...
... generators p = 3 and q = 2. Using the equations for a, b and c we get a = 32 22 = 5, b = 232 = 12, and c = 32 + 22 = ...
MATHEMATICS CURRICULUM FOR PHYSICS
... problems dictated by nature. In this case Mathematics will take on a form of practical applicability rather than being abstract. Bearing in mind the difficulties encountered by teacher of Mathematics in some areas, it is recommended that teachers have regular meetings and consultations among teacher ...
... problems dictated by nature. In this case Mathematics will take on a form of practical applicability rather than being abstract. Bearing in mind the difficulties encountered by teacher of Mathematics in some areas, it is recommended that teachers have regular meetings and consultations among teacher ...
Numbers (TV series)

Numbers (stylized NUMB3RS) is an American crime drama television series that ran on CBS from January 23, 2005, to March 12, 2010. The series was created by Nicolas Falacci and Cheryl Heuton, and follows FBI Special Agent Don Eppes (Rob Morrow) and his brother Charlie Eppes (David Krumholtz) who helps Don solve crimes for the FBI. Brothers Ridley and Tony Scott produced Numb3rs; its production companies are the Scott brothers' Scott Free Productions, CBS Television Studios (originally Paramount Television, and later CBS Paramount Television).The show focuses equally on the relationships among Don Eppes, his brother Charlie Eppes, and their father, Alan Eppes (Judd Hirsch), and on the brothers' efforts to fight crime, normally in Los Angeles. A typical episode begins with a crime, which is subsequently investigated by a team of FBI agents led by Don and mathematically modeled by Charlie, with the help of Larry Fleinhardt (Peter MacNicol) and Amita Ramanujan (Navi Rawat). The insights provided by Charlie's mathematics were always in some way crucial to solving the crime.In May 2010, CBS announced that Numb3rs had been canceled after six seasons.