Irrational numbers
... • Real Numbers are every number. • Therefore, any number that you can find on the number line. ...
... • Real Numbers are every number. • Therefore, any number that you can find on the number line. ...
Ramanujan, Robin, highly composite numbers, and the Riemann
... Nicolas (email to Sondow, 2012): I keep a very strong souvenir of the conference organised in Urbana-Champaign in 1987 for the one hundred anniversary of Ramanujan. It is there that I discovered the hidden part of “Highly Composite Numbers” [first published in [15], later in [16], and again in [2]]. ...
... Nicolas (email to Sondow, 2012): I keep a very strong souvenir of the conference organised in Urbana-Champaign in 1987 for the one hundred anniversary of Ramanujan. It is there that I discovered the hidden part of “Highly Composite Numbers” [first published in [15], later in [16], and again in [2]]. ...
Polygonal Numbers ANSWERS
... one doesn’t look like a triangle, but it would be the triangle that you could make if every side has only one dot.) The second triangle has 2 dots on each side, the third has 3 dots on each side, and so on. If we want to count the number of dots in each triangle, the first one has 1 dot, the second ...
... one doesn’t look like a triangle, but it would be the triangle that you could make if every side has only one dot.) The second triangle has 2 dots on each side, the third has 3 dots on each side, and so on. If we want to count the number of dots in each triangle, the first one has 1 dot, the second ...
Advanced Algebra II Semester #1 Review Questions Handout
... problems and help each other out when someone doesn’t understand a problem/concept. Explaining the material to someone else is a great way to master concepts. Finally, I have all of the lectures on my hard drive if you need to listen to my explanations of certain topics one more time. Bring me a fla ...
... problems and help each other out when someone doesn’t understand a problem/concept. Explaining the material to someone else is a great way to master concepts. Finally, I have all of the lectures on my hard drive if you need to listen to my explanations of certain topics one more time. Bring me a fla ...
module 2 lesosn 8 applying the properties of operations to add and
... Jamal is completing a math problem and represents the expression −5 + 8 − 3 with a single rational number as shown in the steps below. Justify each of Jamal’s steps. Then, show another way to solve the problem. ...
... Jamal is completing a math problem and represents the expression −5 + 8 − 3 with a single rational number as shown in the steps below. Justify each of Jamal’s steps. Then, show another way to solve the problem. ...
Full text
... and will be the subject of a separate paper. 3. Two special sequences of rational numbers, namely the Cauchy numbers of the first kind, Cn , and of the second kind, Ĉn , are closely related to the Bernoulli numbers of the second kind and to the Nörlund numbers, respectively. They appear in Exercis ...
... and will be the subject of a separate paper. 3. Two special sequences of rational numbers, namely the Cauchy numbers of the first kind, Cn , and of the second kind, Ĉn , are closely related to the Bernoulli numbers of the second kind and to the Nörlund numbers, respectively. They appear in Exercis ...
About the cover: Sophie Germain and a problem in number theory
... Germain continued to work on number theory until 1819, well after those cataclysmic events. She wrote regularly to Legendre about her efforts to develop a grand plan to prove Fermat’s Last Theorem (FLT), proving along the way an important special case today called Germain’s Theorem. Legendre was at t ...
... Germain continued to work on number theory until 1819, well after those cataclysmic events. She wrote regularly to Legendre about her efforts to develop a grand plan to prove Fermat’s Last Theorem (FLT), proving along the way an important special case today called Germain’s Theorem. Legendre was at t ...
Sail into Summer with Math! For Students Entering Investigations
... 6. The band had a fundraiser and sold $25,000 worth of candy. They received 40% of this amount for themselves. How much did they receive? ...
... 6. The band had a fundraiser and sold $25,000 worth of candy. They received 40% of this amount for themselves. How much did they receive? ...
Grade 6 Common Core Math Scope and Sequence Draft
... Write an inequality of the form x > c or x < c to represent a constraint or condition in a real-world or mathematical problem. Recognize that inequalities of the form x > c or x < c have infinitely many solutions; represent solutions of such inequalities on number line diagrams (it will take until 4 ...
... Write an inequality of the form x > c or x < c to represent a constraint or condition in a real-world or mathematical problem. Recognize that inequalities of the form x > c or x < c have infinitely many solutions; represent solutions of such inequalities on number line diagrams (it will take until 4 ...
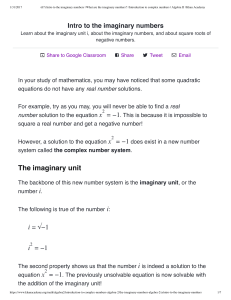
The imaginary unit
... What is (4i) ? https://www.khanacademy.org/math/algebra2/introduction-to-complex-numbers-algebra-2/the-imaginary-numbers-algebra-2/a/intro-to-the-imaginary-numbers ...
... What is (4i) ? https://www.khanacademy.org/math/algebra2/introduction-to-complex-numbers-algebra-2/the-imaginary-numbers-algebra-2/a/intro-to-the-imaginary-numbers ...
Amicable Numbers
... inefficiency of such a sieve with increasing p is given in [5, p. 188]. However, the range for n can be extended by using Alway's method [4] of factorization modified for odd divisors of the form 8fc + 1 and testing each number n -\- 1 individually. ...
... inefficiency of such a sieve with increasing p is given in [5, p. 188]. However, the range for n can be extended by using Alway's method [4] of factorization modified for odd divisors of the form 8fc + 1 and testing each number n -\- 1 individually. ...
Inventing Numbers - American Federation of Teachers
... surprisingly slippery, their sheer slipperiness interesting evidence that certain intellectual tools may be successfully used before they are successfully understood. Numbers tend to sort themselves out by clans or systems, with each new system arising as the result of a perceived infirmity in the o ...
... surprisingly slippery, their sheer slipperiness interesting evidence that certain intellectual tools may be successfully used before they are successfully understood. Numbers tend to sort themselves out by clans or systems, with each new system arising as the result of a perceived infirmity in the o ...
Numbers (TV series)

Numbers (stylized NUMB3RS) is an American crime drama television series that ran on CBS from January 23, 2005, to March 12, 2010. The series was created by Nicolas Falacci and Cheryl Heuton, and follows FBI Special Agent Don Eppes (Rob Morrow) and his brother Charlie Eppes (David Krumholtz) who helps Don solve crimes for the FBI. Brothers Ridley and Tony Scott produced Numb3rs; its production companies are the Scott brothers' Scott Free Productions, CBS Television Studios (originally Paramount Television, and later CBS Paramount Television).The show focuses equally on the relationships among Don Eppes, his brother Charlie Eppes, and their father, Alan Eppes (Judd Hirsch), and on the brothers' efforts to fight crime, normally in Los Angeles. A typical episode begins with a crime, which is subsequently investigated by a team of FBI agents led by Don and mathematically modeled by Charlie, with the help of Larry Fleinhardt (Peter MacNicol) and Amita Ramanujan (Navi Rawat). The insights provided by Charlie's mathematics were always in some way crucial to solving the crime.In May 2010, CBS announced that Numb3rs had been canceled after six seasons.