Download Rational Numbers

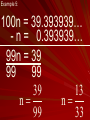
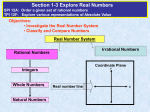
Lesson 5-2 Pages 205-209
Rational
Numbers
Lesson Check 5-1
What you will learn!
1. How to write rational
numbers as fractions.
2. How to identify and classify
rational numbers.
Rational number
What you really need to know!
A number that can be
written as a fraction is a
rational number. Mixed
numbers, integers, and
many decimals can be
written as fractions.
What you really need to know!
Other decimals such a
 = 3.14592654… are
infinite and nonrepeating.
They are called irrational
numbers.
What you really need to know!
Rational
Numbers
1.8
Integers
-5
6
0.7
Whole
Numbers
Natural
Numbers
-12
15
2
1 30
2
3
2
4
5
-3.222…
5
0
-7
4.5
3/4
3/4
5
0
5
Natural
Numbers
Whole
Numbers
-7
0
5
Integers
4.5
-7
0
5
Rational
Numbers
Example 1:
3
Write - 4 as a fraction.
8
-(8 • 4 + 3)
35

8
Example 2:
Write 10 as a fraction.
10
1
Example 3:
Write each decimal as a fraction or
mixed number in simplest form.
26
13

0.26 
100 50
Example 4:
Write each decimal as a fraction or
mixed number in simplest form.
875
7
2.875  2
2
1000
8
Example 5:
Write 0.39 as a fraction in
simplest from.
n = 0.39393939…
100n = 39.393939…
Example 5:
100n = 39.393939…
- n = 0.393939…
99n = 39
99
99
39
13
n
n
99
33
Example 6:
Identify all sets to which
each number belongs.
Natural, Whole,
a. 15 integer, and rational
1
b.
8
Rational number
Example 6:
Identify all sets to which
each number belongs.
c. 0.3030303030…
Rational number
Page 207
Guided Practice
#’s 3-11
Read:
Pages 205-207
with someone at
home and study
examples!
Homework: Pages 208-209
#’s 12-48 even
#’s 52-75
Lesson Check 5-2
Page
733
Lesson 5-2
Lesson Check 5-2