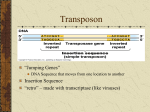
* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Ribinik
Gene therapy wikipedia , lookup
History of genetic engineering wikipedia , lookup
Genome (book) wikipedia , lookup
Gene desert wikipedia , lookup
Epigenetics of human development wikipedia , lookup
Polycomb Group Proteins and Cancer wikipedia , lookup
Gene nomenclature wikipedia , lookup
Protein moonlighting wikipedia , lookup
Vectors in gene therapy wikipedia , lookup
Biology and consumer behaviour wikipedia , lookup
Site-specific recombinase technology wikipedia , lookup
Nutriepigenomics wikipedia , lookup
Smith–Waterman algorithm wikipedia , lookup
Therapeutic gene modulation wikipedia , lookup
Gene therapy of the human retina wikipedia , lookup
Microevolution wikipedia , lookup
Gene expression profiling wikipedia , lookup
Artificial gene synthesis wikipedia , lookup
Assigning Numbers to the Arrows Parameterizing a Gene Regulation Network by using Accurate Expression Kinetics Overview • • • • • • Motivation Gene Regulation Networks Background Our Goal Our Example Parameterizing Algorithm Results Motivation • Understand regulation factors for different genes • Can help understand a gene’s function • If we can understand how it all works we can use it for medical purposes like fixing and preventing DNA damage! Background: Gene Regulation Networks(1) • Dynamically orchestrate the level of expression for each gene • How? Control whether and how vigorously that gene will be transcribed into RNA (biological stuff) Background: Gene Regulation Networks(2) • Contains: 1. Input Signals: environmental cues, intracellular signals 2. Regulatory Proteins 3. Target Genes Our Goal • Assign parameters to a Gene Regulation Network based on experiments: - production of unrepressed promoter. the maximum production k- concentration of repressor at half maximal repression. The bigger it is the earlier the earlier the gene becomes active and the later it becomes inactive again Our Example(1) • Escheria coli bacterium • SOS DNA repair system – used to repair damage done by UV light • 8 (out of about 30) gene groups (operons) Our Example(2) • Simple network architecture – recall what we saw last week: SIM (Single Input Module) • All genes are under negative control of a single repressor (a protein that reduces gene levels) A X1 X2 ... Xn Parametrization Algorithm Definitions: X ij (t ) - the activity of promoter i in experiment j as function of time A j (t ) - effective repressor concentration in experiment j as function of time i - production rate of the unrepressed promoter i k i - k parameter of promoter i Parametrization Algorithm 1: Trial Function [1] : X ij (t ) i (1 Aj (t ) / ki ) Why? Michaelis-Menten form: a very useful equation in modeling biological behavior. Parametrization Algorithm 2: Data Preprocessing(1) • Smoothing the signals using a hybrid Gaussian-median filter with a window size of five measurements: Five time points are taken, sorted and the average of central three points is taken to be the signal. Parametrization Algorithm 2: Data Preprocessing(2) Some more definitions: X i (t ) - the activity of promoter i as a function of time Gi (t ) - GFP fluorescence from the corresponding reporter as a function of time ODi (t ) - corresponding Optical Density as a function of time Parametrization Algorithm 2: Data Preprocessing(3) • The signal is smooth enough to be differentiated • The activity of promoter i is proportional to the number of GFP molecules produced per unit time per cell X i (t ) [dGi (t ) / dt ] / ODi (t ) Parametrization Algorithm 2: Data Preprocessing(4) • The activity signal is smoothed by a polynomial fit of sixth order to: log[ X i (t )] • The smoothing procedure captures the dynamics well, while removing noise • Data for all experiments is concatenated and normalized by the maximal activity for each operon Parametrization Algorithm 3: Parameter Determination(1) • To determine parameters in equation [1] based on experimental data we transform it into a bilinear form: 1 ui (t ) ai A(t ) bi X i (t ) where: 1 ai i ki bi 1 i Parametrization Algorithm 3: Parameter Determination(2) • Now, the matrix X i (t ) N M where N is for genes and M for time points, is modeled by two vectors of size N: ai , bi and one vector of size M: A(t ) • 2N*M variables Parametrization Algorithm 3: Parameter Determination(3) – some algebra • The standard method of least mean squares solution for such a problem uses SVD (Singular Value Decomposition) • The mean over i of ui (t ) is removed: ui (t ) ui (t ) mean(ui (t )) Parametrization Algorithm 3: Parameter Determination(4) – some algebra • A(t) is the SVD eigenvector with the largest eigenvalue of the matrix: J (t , t ' ) ui (t ) ui (t ' ) i This is the covariance matrix • Results for A(t) are normalized to fit the constraints: A(t 0) 1, min( A(t )) 0 • Alternative normalization: add points with A=0 and X i Parametrization Algorithm 3: Parameter Determination(5) – some algebra • Perform a second round of optimization for i , ki by using a nonlinear least mean squares solver to minimize ( X measured X predicted )2 Parametrization Algorithm 4: Error Evaluation(1) • The mean error for promoter i is given by: T 1 Ei T t 1 X itmeasured X itpredicted X itmeasured where T is the total time of the experiment • This is considered the quality of the data model in describing the data Parametrization Algorithm 4: Error Evaluation(2) • The error estimate for the parameters is determined by using a graphic method: 1 A(t ) 1 ai A(t ) bi X i (t ) i ki i is plotted vs. A(t) Parametrization Algorithm 4: Error Evaluation(3) • From maximal and minimal slopes of the 1 graphs the error for ai is determined i ki • From maximal and minimal intersections with 1 the y axis the error for is determined i Parametrization Algorithm 5: Additional Trial Function(1) • An extension of the model to the case of cooperative binding – a regulator can be a repressor for some genes and an activator for others, and with different measures: X ij (t ) i 1 ( Aj (t ) / ki ) H i Parametrization Algorithm 5: Additional Trial Function(2) H i -Hill coefficient for operon i Hill coefficient? A coefficient that describes binding H i 0 - repression H i 0 - activation H i 1 - no cooperation Parametrization Algorithm 5: Additional Trial Function(3) Our example: good comparison between measured results and those calculated with H i 1 trial function suggest there may be no significant cooperativity in the repressor action Results: Promoter Activity Profiles(1) • After about half a cell cycle the promoter activities begin to decrease • Corresponds to the repair of damaged DNA Results: Promoter Activity Profiles(2) • The mean error between repeat experiments performed of different days is about 10% Results: Assigning Effective Kinetic Parameters • The error is under 25% for most promoters Results: Detection of Promoters with Additional Regulation • Relatively large error may help to detect operons that have additional regulation. • Examples: 1. lacZ – very large error (150%) 2. uvrY – recently found to participate in another system and to be regulated by other transcription factors (45% error) Results: Determining Dynamics of an Entire System Based on a Single Representative(1) • Once the parameters are determined for each operon, we need to measure only the dynamics of one promoter in a new experiment to estimate all other SOS promoter kinetics X m (t ) 1 m kn n ( k m X n (t ) 1) Results: Determining Dynamics of an Entire System Based on a Single Representative(2) • The estimated kinetics using data from only one of the operons agree quite well with the measured kinetics for all operons • Same level of agreement found by using different operons as the base operon Results: Determining Dynamics of an Entire System Based on a Single Representative(3) Results: Repressor Protein Concentration Profile • Current measurements don’t directly measure the concentration of the proteins produced by these operons, only the rate at which the corresponding mRNA’s are produced • The parameterization algorithm allows calculation of the transcriptional repressor A(t), directly. Summary • We can apply the current method to any SIM motif, in gene regulation networks • The method won’t work with multiple regulatory factors Questions? Thank You For Listening!