Download Neuronal Modeling

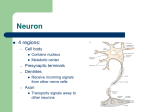
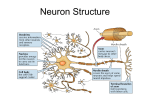
Computational Biology, Part 20
Neuronal Modeling
Robert F. Murphy
Copyright  1996, 1999, 2001.
All rights reserved.
Basic Neurophysiology
An imbalance of charge across a membrane
is called a membrane potential
 The major contribution to membrane
potential in animal cells comes from
imbalances in small ions (e.g., Na, K)
 The maintainance of this imbalance is an
active process carried out by ion pumps

Basic Neurophysiology
The cytoplasm of most cells (including
neurons) has an excess of negative ions over
positive ions (due to active pumping of
sodium ions out of the cell)
 By convention this is referred to as a
negative membrane potential (inside
minus outside)
 Typical resting potential is -50 mV

Basic Neurophysiology
Ion pumps require energy (ATP) to carry
ions across a membrane up a concentration
gradient (they generate a potential)
 Ion channels allow ions to flow across a
membrane down a concentration gradient
(they dissipate a potential)

Basic Neurophysiology
A cell is said to be electrically polarized
when it has a non-zero membrane potential
 A dissipation (partial or total) of the
membrane potential is referred to as a
depolarization, while restoration of the
resting potential is termed repolarization

Basic Neurophysiology
Ion channels can switch between open and
closed states
 If an ion channel can switch its state due to
changes in membrane potential, it is said to
be voltage-sensitive
 A membrane containing voltage-sensitive
ion channels and/or ion pumps is said to be
an excitable membrane

Basic Neurophysiology

An idealized neuron consists of
 soma
or cell body
 contains
nucleus and performs metabolic functions
 dendrites
 receive
signals from other neurons through synapses
 axon
 propagates
 terminal
 form
signal away from soma
branches
synapses with other neurons
Basic Neurophysiology
The junction between the soma and the axon
is called the axon hillock
 The soma sums (“integrates”) currents
(“inputs”) from the dendrites
 When the received currents result in a
sufficient change in the membrane potential,
a rapid depolarization is initiated in the axon
hillock

Basic Neurophysiology
The depolarization is caused by opening of
voltage-sensitive sodium channels that
allow sodium ions to flow into the cell
 The sodium channels only open in response
to a partial depolarization, such that a
threshold voltage is exceeded

Basic Neurophysiology
As sodium floods in, the membrane
potential reverses, such that the interior is
now positive relative to the outside
 This positive potential causes voltagesensitive potassium channels to open,
allowing K+ ions to flow out
 The potential overshoots (becomes more
negative than) the resting potential

Basic Neurophysiology
The fall in potential triggers the sodium
channels to close, setting the stage for
restoration of the resting potential by
sodium pumps
 This sequential depolarization, polarity
reversal, potential overshoot and
repolarization is called an action potential

Action Potential
Stim ulus
(uA)
15 0
10 0
50
0
60
Voltage (mV)
40
20
0
-20
-40
-60
-80
Conductance
(mS/cm2)
40
G(Na)
30
G(K)
20
10
0
0
2
4
Time (m s)
6
8
10
Basic Neurophysiology
The depolarization in the axon hillock
causes a depolarization in the region of the
axon immediately adjacent to the hillock
 Depolarization (and repolarization)
proceeds down the axon until it reaches the
terminal branches, which release
neurotransmitters to stimulate neurons
with which they form synapses

Basic Neurophysiology
These sequential depolarizations form a
traveling wave passing down the axon
 Note that while a signal is passed down the
axon, it is not comparable to an electrical
signal traveling down a cable

Basic Neurophysiology

Current flows in an electrical cable
 are
in the direction that the signal is propagating
 consist of electrons

Current flows in a neuron
 are
transverse to the signal propagation
 consist of positively-charged ions
The Hodgkin-Huxley Model
Based on electrophysiological
measurements of giant squid axon
 Empirical model that predicts experimental
data with very high degree of accuracy
 Provides insight into mechanism of action
potential

The Hodgkin-Huxley Model

Define
 voltage across the membrane at time t
 q(t) net charge inside the neuron at t
 I(t) current of positive ions into neuron at t
 g(v) conductance of membrane at voltage v
 C capacitance of the membrane
 Subscripts Na, K and L used to denote specific
currents or conductances (L=“other”)
 v(t)
The Hodgkin-Huxley Model

Start with equation for capacitor
v(t ) 
q(t )
C
The Hodgkin-Huxley Model

Consider each ion separately and sum
currents to get rate of change in charge and
hence voltage
dq
 I Na  I K  I L
dt
I Na  g Na (v  v Na )
I K  g K (v  v K )
I L  gL ( v  vL )
dv
dt

1
C
g Na ( v)(v  v Na )  g K ( v)( v  v K )  g L (v  v L ) 
The Hodgkin-Huxley Model

Central concept of model: Define three state
variables that represent (or “control”) the
opening and closing of ion channels
m
controls Na channel opening
 h controls Na channel closing
 n controls K channel opening
The Hodgkin-Huxley Model

Define relationship of state variables to
conductances of Na and K
g Na  g Na m h
3
gK  gK n 4
0  m, n, h  1
The Hodgkin-Huxley Model
Can write differentials for m,n,h with
respect to t
 Gives set of four coupled, non-linear,
ordinary differential equations
 Must be integrated numerically

Hodgkin-Huxley Gates
Stim ulus
(uA)
15 0
10 0
50
0
60
Voltage (mV)
40
20
0
-20
-40
-60
-80
Gate param
va lue
1.0
0.8
m gate (Na)
0.6
h gate (Na)
0.4
n gate (K)
0.2
0.0
0
2
4
Time (m s)
6
8
10
Interactive demonstration

(Integration of Hodgin-Huxley equations
using Maple)