* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Neuronal Modeling
Theories of general anaesthetic action wikipedia , lookup
Cytokinesis wikipedia , lookup
Organ-on-a-chip wikipedia , lookup
SNARE (protein) wikipedia , lookup
Cyclic nucleotide–gated ion channel wikipedia , lookup
List of types of proteins wikipedia , lookup
Signal transduction wikipedia , lookup
Endomembrane system wikipedia , lookup
Cell membrane wikipedia , lookup
Node of Ranvier wikipedia , lookup
Chemical synapse wikipedia , lookup
Mechanosensitive channels wikipedia , lookup
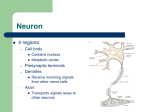
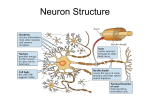
Computational Biology, Part 20 Neuronal Modeling Robert F. Murphy Copyright 1996, 1999, 2001. All rights reserved. Basic Neurophysiology An imbalance of charge across a membrane is called a membrane potential The major contribution to membrane potential in animal cells comes from imbalances in small ions (e.g., Na, K) The maintainance of this imbalance is an active process carried out by ion pumps Basic Neurophysiology The cytoplasm of most cells (including neurons) has an excess of negative ions over positive ions (due to active pumping of sodium ions out of the cell) By convention this is referred to as a negative membrane potential (inside minus outside) Typical resting potential is -50 mV Basic Neurophysiology Ion pumps require energy (ATP) to carry ions across a membrane up a concentration gradient (they generate a potential) Ion channels allow ions to flow across a membrane down a concentration gradient (they dissipate a potential) Basic Neurophysiology A cell is said to be electrically polarized when it has a non-zero membrane potential A dissipation (partial or total) of the membrane potential is referred to as a depolarization, while restoration of the resting potential is termed repolarization Basic Neurophysiology Ion channels can switch between open and closed states If an ion channel can switch its state due to changes in membrane potential, it is said to be voltage-sensitive A membrane containing voltage-sensitive ion channels and/or ion pumps is said to be an excitable membrane Basic Neurophysiology An idealized neuron consists of soma or cell body contains nucleus and performs metabolic functions dendrites receive signals from other neurons through synapses axon propagates terminal form signal away from soma branches synapses with other neurons Basic Neurophysiology The junction between the soma and the axon is called the axon hillock The soma sums (“integrates”) currents (“inputs”) from the dendrites When the received currents result in a sufficient change in the membrane potential, a rapid depolarization is initiated in the axon hillock Basic Neurophysiology The depolarization is caused by opening of voltage-sensitive sodium channels that allow sodium ions to flow into the cell The sodium channels only open in response to a partial depolarization, such that a threshold voltage is exceeded Basic Neurophysiology As sodium floods in, the membrane potential reverses, such that the interior is now positive relative to the outside This positive potential causes voltagesensitive potassium channels to open, allowing K+ ions to flow out The potential overshoots (becomes more negative than) the resting potential Basic Neurophysiology The fall in potential triggers the sodium channels to close, setting the stage for restoration of the resting potential by sodium pumps This sequential depolarization, polarity reversal, potential overshoot and repolarization is called an action potential Action Potential Stim ulus (uA) 15 0 10 0 50 0 60 Voltage (mV) 40 20 0 -20 -40 -60 -80 Conductance (mS/cm2) 40 G(Na) 30 G(K) 20 10 0 0 2 4 Time (m s) 6 8 10 Basic Neurophysiology The depolarization in the axon hillock causes a depolarization in the region of the axon immediately adjacent to the hillock Depolarization (and repolarization) proceeds down the axon until it reaches the terminal branches, which release neurotransmitters to stimulate neurons with which they form synapses Basic Neurophysiology These sequential depolarizations form a traveling wave passing down the axon Note that while a signal is passed down the axon, it is not comparable to an electrical signal traveling down a cable Basic Neurophysiology Current flows in an electrical cable are in the direction that the signal is propagating consist of electrons Current flows in a neuron are transverse to the signal propagation consist of positively-charged ions The Hodgkin-Huxley Model Based on electrophysiological measurements of giant squid axon Empirical model that predicts experimental data with very high degree of accuracy Provides insight into mechanism of action potential The Hodgkin-Huxley Model Define voltage across the membrane at time t q(t) net charge inside the neuron at t I(t) current of positive ions into neuron at t g(v) conductance of membrane at voltage v C capacitance of the membrane Subscripts Na, K and L used to denote specific currents or conductances (L=“other”) v(t) The Hodgkin-Huxley Model Start with equation for capacitor v(t ) q(t ) C The Hodgkin-Huxley Model Consider each ion separately and sum currents to get rate of change in charge and hence voltage dq I Na I K I L dt I Na g Na (v v Na ) I K g K (v v K ) I L gL ( v vL ) dv dt 1 C g Na ( v)(v v Na ) g K ( v)( v v K ) g L (v v L ) The Hodgkin-Huxley Model Central concept of model: Define three state variables that represent (or “control”) the opening and closing of ion channels m controls Na channel opening h controls Na channel closing n controls K channel opening The Hodgkin-Huxley Model Define relationship of state variables to conductances of Na and K g Na g Na m h 3 gK gK n 4 0 m, n, h 1 The Hodgkin-Huxley Model Can write differentials for m,n,h with respect to t Gives set of four coupled, non-linear, ordinary differential equations Must be integrated numerically Hodgkin-Huxley Gates Stim ulus (uA) 15 0 10 0 50 0 60 Voltage (mV) 40 20 0 -20 -40 -60 -80 Gate param va lue 1.0 0.8 m gate (Na) 0.6 h gate (Na) 0.4 n gate (K) 0.2 0.0 0 2 4 Time (m s) 6 8 10 Interactive demonstration (Integration of Hodgin-Huxley equations using Maple)