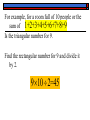Download Notes 2.7 – Rational Functions

Notes 1.1 – Representing
Number Patterns
I. Problem
10 people in a room are instructed to shake hands
with each other. How many handshakes would
be required for each person to shake hands
with each person 1 time?
Ideas?
Let’s start with a smaller number of people
and work our way up to 10.
People
Shakes
1
0
3
3
2
1
+1
+2
See a pattern developing?
4
6
+3
5
10
+4
Why?
Every time someone new enters the room,
everyone else must shake their hand.
People
Shakes
6 7 8 9 10
15 21 28 36 45
+5 +6
+7
+8
+9
II. Making a Conjecture
A ____________is
a statement based on
conjecture
observation that is believed to be _______.
TRUE
What would your conjecture be? Write it down
now.
The total number of handshakes among any
number of students is the sum of the numbers
from 1 to one less than the number of people in
the room.
III. Your Turn…
Example 1 – A football conference consists of 8
teams. How many games will be played in a
season if each team is to play every other
team in the conference exactly one time?
Almost exactly like the handshake situation,
right?
1+2+3+4+5+6+7= 28!!!
The shortcut…
Notice that this is a ________
of what we call an
sum
__________
arithmetic _________–
sequence a pattern of numbers
that increases by a constant sum. There is a
mathematical formula for this.
first number + last number
sum=
 the number of terms
2
1+7
8
sum=
 7   7  4  7  28
2
2
IV. Sequences
A ____________
SEQUENCE is any arrangement of
numbers that shows a pattern
Example # term 1
2
3
4
5
6
…
Term
1
3
6
10
15
…
0
… means the sequence
continues
V. Examples
Predict the next three terms of each sequence.
A.) 13,16,19, 22,...
Pattern :
3, 3, 3,...
25, 28,31
B.) 1,3,7,13,21,...
Pattern :
2, 4, 6, 8, 10, 12, 14
31, 43,57
VI. Rectangular and Triangular
Numbers
Rectangular __________are
Numbers
___________
a sequence of numbers
RECTANGLE
that can be visualized as a ______________.
Determine how many dots would be in the next
figure.
1x2
2x3
3x4
4x5
So…the next rectangle would be…
Triangular Numbers: Numbers that can be
visualized by a _____________.
TRIANGLE
1x2 ÷2
2x3÷2
3x4÷2
4x5÷2
Determine how many dots would be in the next
figure.
Notice how the triangular numbers are the same
numbers from the handshake problem.
1,3,6,10,...
Remember when we added the numbers all the
way up to one less than the number of people?
0+1+2+3+4+5+6+7+8+9=45
This gives us another way to find the sum of a
set of consecutive numbers!!!
First, find the __________
rectangular _______
number associated
with the term, and then ________
divide it by ____.
2
For example, for a room full of 10 people or the
sum of 1+2+3+4+5+6+7+8+9
Is the triangular number for 9.
Find the rectangular number for 9 and divide it
by 2.
9 10  2=45
Your turn…
1.) Find the 15th triangular number.
15 16  2=120
2.) Find the sum of the numbers 1 through 100.
100 101  2=5050
3.) How many handshakes would take place
between 20 people?
20 19  2=190