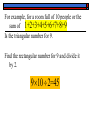* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Notes 2.7 – Rational Functions
Foundations of mathematics wikipedia , lookup
Positional notation wikipedia , lookup
Law of large numbers wikipedia , lookup
Infinitesimal wikipedia , lookup
Ethnomathematics wikipedia , lookup
Georg Cantor's first set theory article wikipedia , lookup
Location arithmetic wikipedia , lookup
Non-standard analysis wikipedia , lookup
Surreal number wikipedia , lookup
Bernoulli number wikipedia , lookup
Hyperreal number wikipedia , lookup
Real number wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Large numbers wikipedia , lookup
Series (mathematics) wikipedia , lookup
Proofs of Fermat's little theorem wikipedia , lookup
Collatz conjecture wikipedia , lookup
Notes 1.1 – Representing Number Patterns I. Problem 10 people in a room are instructed to shake hands with each other. How many handshakes would be required for each person to shake hands with each person 1 time? Ideas? Let’s start with a smaller number of people and work our way up to 10. People Shakes 1 0 3 3 2 1 +1 +2 See a pattern developing? 4 6 +3 5 10 +4 Why? Every time someone new enters the room, everyone else must shake their hand. People Shakes 6 7 8 9 10 15 21 28 36 45 +5 +6 +7 +8 +9 II. Making a Conjecture A ____________is a statement based on conjecture observation that is believed to be _______. TRUE What would your conjecture be? Write it down now. The total number of handshakes among any number of students is the sum of the numbers from 1 to one less than the number of people in the room. III. Your Turn… Example 1 – A football conference consists of 8 teams. How many games will be played in a season if each team is to play every other team in the conference exactly one time? Almost exactly like the handshake situation, right? 1+2+3+4+5+6+7= 28!!! The shortcut… Notice that this is a ________ of what we call an sum __________ arithmetic _________– sequence a pattern of numbers that increases by a constant sum. There is a mathematical formula for this. first number + last number sum= the number of terms 2 1+7 8 sum= 7 7 4 7 28 2 2 IV. Sequences A ____________ SEQUENCE is any arrangement of numbers that shows a pattern Example # term 1 2 3 4 5 6 … Term 1 3 6 10 15 … 0 … means the sequence continues V. Examples Predict the next three terms of each sequence. A.) 13,16,19, 22,... Pattern : 3, 3, 3,... 25, 28,31 B.) 1,3,7,13,21,... Pattern : 2, 4, 6, 8, 10, 12, 14 31, 43,57 VI. Rectangular and Triangular Numbers Rectangular __________are Numbers ___________ a sequence of numbers RECTANGLE that can be visualized as a ______________. Determine how many dots would be in the next figure. 1x2 2x3 3x4 4x5 So…the next rectangle would be… Triangular Numbers: Numbers that can be visualized by a _____________. TRIANGLE 1x2 ÷2 2x3÷2 3x4÷2 4x5÷2 Determine how many dots would be in the next figure. Notice how the triangular numbers are the same numbers from the handshake problem. 1,3,6,10,... Remember when we added the numbers all the way up to one less than the number of people? 0+1+2+3+4+5+6+7+8+9=45 This gives us another way to find the sum of a set of consecutive numbers!!! First, find the __________ rectangular _______ number associated with the term, and then ________ divide it by ____. 2 For example, for a room full of 10 people or the sum of 1+2+3+4+5+6+7+8+9 Is the triangular number for 9. Find the rectangular number for 9 and divide it by 2. 9 10 2=45 Your turn… 1.) Find the 15th triangular number. 15 16 2=120 2.) Find the sum of the numbers 1 through 100. 100 101 2=5050 3.) How many handshakes would take place between 20 people? 20 19 2=190