* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download NEURAL NETWORKS
Neural coding wikipedia , lookup
Neural oscillation wikipedia , lookup
Optogenetics wikipedia , lookup
Biological neuron model wikipedia , lookup
Neural modeling fields wikipedia , lookup
Neuroeconomics wikipedia , lookup
Holonomic brain theory wikipedia , lookup
Neuropsychopharmacology wikipedia , lookup
Synaptic gating wikipedia , lookup
Pattern recognition wikipedia , lookup
Central pattern generator wikipedia , lookup
Neural binding wikipedia , lookup
Metastability in the brain wikipedia , lookup
Neural engineering wikipedia , lookup
Development of the nervous system wikipedia , lookup
Artificial neural network wikipedia , lookup
Nervous system network models wikipedia , lookup
Catastrophic interference wikipedia , lookup
Convolutional neural network wikipedia , lookup
NEURAL NETWORKS
Vedat Tavşanoğlu
What Is a Neural Network?
Work on artificial neural networks,
commonly referred to as "neural networks,"
has been motivated right from its inception
by the recognition that the brain computes
in an entirely different way from the
conventional digital computer.
What Is a Neural Network?
The struggle to understand the brain owes much
to the pioneering work of Ramon y Cajal (1911),
who introduced the idea of neurons as structural
constituents of the brain.
Typically, neurons are five to six orders of
magnitude slower than silicon logic gates; events
in a silicon chip happen in the nanosecond (10-9 s)
range, whereas neural events happen in the
millisecond (10-3 s) range.
What Is a Neural Network?
However, the brain makes up for the
relatively slow rate of operation of a neuron
by having a truly staggering number of
neurons (nerve cells) with massive
interconnections between them.
What Is a Neural Network?
It is estimated that there must be on the order of
10 billion neurons in the human cortex, and 60
trillion synapses or connections (Shepherd and
Koch, 1990). The net result is that the brain is an
enormously efficient structure. Specifically, the
energetic efficiency of the brain is approximately
10-16 joules (J) per operation per second.
The corresponding value for the best computers
in use today is about 10-6 joules per operation per
second (Faggin, 1991).
What Is a Neural Network?
The brain is a highly complex, nonlinear,
and parallel computer (informationprocessing system). It has the capability of
organizing neurons so as to perform certain
computations (e.g., pattern recognition,
perception, and motor control) many times
faster than the fastest digital computer in
existence today.
What Is a Neural Network?
Consider, for example, human vision, which is an
information-processing task (Churchland and
Sejnowski, 1992; Levine, 1985; Marr, 1982).
It is the function of the visual system to provide a
representation of the environment around us and,
more important, to supply the information we
need to interact with the environment.
What Is a Neural Network?
The brain routinely accomplishes perceptual
recognition tasks (e.g., recognizing a
familiar face embedded in an unfamiliar
scene) in something of the order of 100-200
ms, whereas tasks of much lesser complexity
will take hours on conventional computers.
What Is a Neural Network?
For another example, consider the sonar of a bat.
Sonar is an active echo-location system.
In addition to providing information about how far
away a target (e.g., a flying insect) is, a bat sonar
conveys information about the relative velocity of
the target, the size of the target, the size of various
features of the target, and the azimuth and
elevation of the target (Suga, 1990a, b).
What Is a Neural Network?
The complex neural computations needed to
extract all this information from the target
echo occur within a brain the size of a plum.
Indeed, an echo-locating bat can pursue and
capture its target with a facility and success
rate that would be the envy of a radar or
sonar engineer.
What Is a Neural Network?
How, then, does a human brain or the brain
of a bat do it?
At birth, a brain has great structure and the
ability to build up its own rules through
what we usually refer to as "experience."
What Is a Neural Network?
Indeed, experience is built up over the years,
with the most dramatic development (i.e.,'·
hard-wiring) of the human brain taking place
in the first two years from birth; but the
development continues well beyond that stage.
During this early stage of development, about 1
million synapses are formed per second.
What Is a Neural Network?
Synapses are elementary structural and
functional units that mediate the
interactions between neurons. The most
common kind of synapse is a chemical
synapse, which operates as follows:
What Is a Neural Network?
A presynaptic process liberates a transmitter
substance that diffuses across the synaptic
junction between neurons and then acts on a
postsynaptic process.
Thus a synapse converts a presynaptic
electrical signal into a chemical signal and
then back into a postsynaptic electrical
signal (Shepherd and Koch, 1990).
What Is a Neural Network?
In electrical terminology, such an element is
said to be a nonreciprocal two-port device.
In traditional descriptions of neural
organization, it is assumed that a synapse is
a simple connection that can impose
excitation or inhibition, but not both on the
receptive neuron.
What Is a Neural Network?
A developing neuron is synonymous with a plastic
brain: Plasticity ([Latin plasticus, from Greek
plastikos, from plastos, molded, from plassein, to
mold; see pelə-2 in Indo-European roots.] )permits
the developing nervous system to adapt to its
surrounding environment (Churchland and
Sejnowski, 1992; Eggermont, 1990). In an adult
brain, plasticity may be accounted for by two
mechanisms: the creation of new synaptic
connections between neurons, and the
modification of existing synapses.
What Is a Neural Network?
Axons, the transmission lines, and dendrites, the
receptive zones, constitute two types of cell
filaments that are distinguished on morphological
grounds; an axon has a smoother surface, fewer
branches, and greater length, whereas a dendrite
(so called because of its resemblance to a tree)
has an irregular surface and more branches
(Freeman, 1975).
What Is a Neural Network?
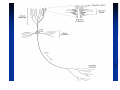
Neurons come in a wide variety of shapes
and sizes in different parts of the brain. The
figure illustrates the shape of a pyramidal
cell, which is one of the most common types
of cortical neurons.
Like many other types of neurons, it receives
most of its inputs through dendritic spines.
The pyramidal cell can receive 10,000 or
more synaptic contacts and it can project
onto thousands of target cells.
What Is a Neural Network?
Just as plasticity appears to be essential to the
functioning of neurons as informationprocessing
units in the human brain, so it is with neural
networks made up of artificial neurons.
What Is a Neural Network?
In its most general form, a neural network is
a machine that is designed to model the way
in which the brain performs a particular task
or function of interest; the network is usually
implemented using electronic components
or simulated in software on a digital
computer.
What Is a Neural Network?
In most cases the interest is confined largely
to an important class of neural networks that
perform useful computations through a
process of learning.
What Is a Neural Network?
To achieve good performance, neural
networks employ a massive interconnection
of simple computing cells referred to as
"neurons" or "processing units." We may
thus offer the following definition of a neural
network viewed as an adaptive machine:
What Is a Neural Network?
A neural network is a massively parallel distributed
processor that has a natural propensity for storing
experiential knowledge and making it available for use.
It resembles the brain in two respects:
1 Knowledge is acquired by the network
through a learning process .
2
Interneuron connection strengths known as
synaptic weights are used to store the knowledge.
What Is a Neural Network?
The procedure used to perform the learning
process is called a learning algorithm,
the function of which is to modify the synaptic
weights of the network
in an orderly fashion so as to attain a desired
design objective.
What Is a Neural Network?
The modification of synaptic weights provides the
traditional method for the design of neural
networks. Such an approach is the closest to
linear adaptive filter theory, which is already well
established and successfully applied in such
diverse fields as communications, control, radar,
sonar, seismology, and biomedical engineering
(Haykin, 1991; Widrow and Stearns, 1985).
What Is a Neural Network?
However, it is also possible for a neural
network to modify its own topology, which
is motivated by the fact that neurons in the
human brain can die and that new synaptic
connections can grow.
What Is a Neural Network?
Neural networks are also referred to in the
literature as neurocomputers, connectionist
networks, parallel distributed processors,
etc.
Benefits of Neural Networks
From the above discussion, it is apparent that a
neural network derives its computing power
through:
1.
its massively parallel distributed structure,
1.
its ability to learn and therefore generalize;
generalization refers to the neural network
producing reasonable outputs for inputs not
encountered during training (learning).
Benefits of Neural Networks
How does the following example help you to generalize ?
confer: L. conferre- con-, together, ferre, to bring
v.t. to give, to bestow (to place or put by), to talk or consult together
defer: L. differre- dis-, asunder (adv. apart, into parts, separately), ferre, to bear , to carry
v.t. to put off to another time, to delay
defer: L. deferre- de-, down, ferre, to bear
v.i. to yield (to the wishes or opinions of another, or to authority), v.t. to submit or
to or to lay before somebody
differ: L. differre- dif.( for dis-), apart, ferre, to bear
v.i. to be unlike, distinct or various
infer: L. inferre- in-, into, ferre, to bring
v.t.. to bring on, to drive as a conclusion
prefer: L. preaferre- prea-,in front of, ferre, to bear
v.t. to set in front, to put forward, offer, submit, present, for acceptance or consideration,
to promote
Benefits of Neural Networks
convene L. convenire, con- together, and venire, to come
v.i. to come together, v.i. to call together
convent v.t. to convene
convention the act of convening, :an assembly, esp. of
special delegates for some common object, an agreement
(Geneva Convention)
invent L. invenire, inventum, in-, upon, venire, to come
v.t. to find, to device or contrive
prevent L. preavenire, prea- in front of, venire, to come
v.t. to precede, to be, go, act, earlier than, to preclude, to stop,
keep, or hinder effectually, to keep from coming to pass
Benefits of Neural Networks
Synonym:1432 (but rare before 18c.), from L.
synonymum, from Gk. synonymon "word having the
same sense as another," noun use of neut. of
synonymos "having the same name as,
synonymous," from syn- "together, same" +
onyma, Aeolic dialectal form of onoma "name"
(see name). Synonymous is attested from 1610.
Benefits of Neural Networks
Antonym:1870, created to serve as opposite of
synonym, from Gk. anti- "equal to, instead of,
opposite" (see anti-) + -onym "name" (see name).
Anonymous:1601, from Gk. anonymos "without a
name," from an- "without" + onyma, Æolic
dialectal form of onoma "name" (see name).
Benefits of Neural Networks
These two information-processing
capabilities,i.e.,
(1) massively parallel distributed structure
(2) the ability to generalize
make it possible for neural networks to solve
complex (large-scale) problems that are
currently intractable. In practice, however,
neural networks cannot provide the solution
working by themselves alone. Rather, they need
to be integrated into a consistent system
engineering approach.
Benefits of Neural Networks
1.
2.
3.
Specifically, a complex problem of interest is
decomposed into a number of relatively simple tasks,
and neural networks are assigned a subset of the tasks
e.g.,
pattern recognition,
associative memory,
control,etc.
that match their inherent capabilities. It is important to
recognize, however, that we have a long way to go (if
ever) before we can build a computer architecture that
mimics the human brain.
Properties and Capabilities of Neural
Networks
1. Nonlinearity
A neuron is basically a nonlinear device.
Consequently, a neural network, made up of an
interconnection of neurons, is itself nonlinear.
Moreover, the nonlinearity is of a special kind in
the sense that it is distributed throughout the
network. Nonlinearity is a highly important
property, particularly if the underlying physical
mechanism responsible for the generation of an
input signal (e.g., speech signal) is inherently
nonlinear.
Properties and Capabilities of Neural
Networks
2. Input-Output Mapping
A popular paradigm of learning called
supervised learning involves the modification
of the synaptic weights of a neural network by
applying a set of labeled training samples or
task examples. Each example consists of a
unique input signal and the corresponding
desired response.
Properties and Capabilities of Neural
Networks
The network is presented an example picked at
random from the set,
and
the synaptic weights(free parameters) of the
network are modified so as to minimize the
difference between the desired response and the
actual response of the network
Properties and Capabilities of Neural
Networks
The training of the network is repeated for many
examples in the set until the network reaches a
steady state, where there are no further significant
changes in the synaptic weights;
The previously applied training examples may be
reapplied during the training session but in a
different order.
Properties and Capabilities of
Neural Networks
Thus the network learns from the examples by
constructing an input-output mapping for the
problem at hand.
Properties and Capabilities of Neural
Networks
Such an approach brings to mind the study of
nonparametric statistical inference which is a branch of
statistics dealing with model-free estimation, or, from a
biological viewpoint, tabula rasa learning (Geman et al.,
1992).
(tabula rasa: a smoothed or blank tablet, a mind not yet
influenced by outside impressions and experiences)
([Medieval Latin tabula rāsa : Latin tabula, tablet + Latin
rāsa, feminine of rāsus, erased.]
Properties and Capabilities of
Neural Networks
Consider, for example, a pattern classification task,
where the requirement is to assign an input signal
representing a physical object or event to one of several
prespecified categories (classes).
In a nonparametric approach to this problem, the
requirement is to "estimate" arbitrary decision
boundaries in the input signal space for the patternclassification task using a set of examples, and to do so
without invoking a probabilistic distribution model.
Properties and Capabilities of Neural
Networks
A similar point of view is implicit in the
supervised learning paradigm, which suggests
a close analogy between the input-output
mapping performed by a neural network and
nonparametric statistical inference.
paradigm:1.Grammar. a.a set of forms all of which
contain a particular element, esp. the set of all
inflected forms based on a single stem or theme.
b.a display in fixed arrangement of such a set, as
boy, boy's, boys, boys'. 2.an example serving as a
model; pattern. [Origin: 1475–85; < LL paradīgma
< Gk parádeigma pattern (verbid of paradeiknýnai
to show side by side), equiv. to para- para-1 + deik, base of deiknýnai to show (see deictic) + -ma n.
suffix ]
Properties and Capabilities of Neural
Networks
analogy: 1550, from L. analogia, from Gk.
analogia "proportion," from ana- "upon,
according to" + logos "ratio," also "word,
speech, reckoning." A mathematical term
used in a wider sense by Plato.
Properties and Capabilities of Neural
Networks
3. Adaptivity.
Neural networks have a built-in capability to
adapt their synaptic weights to changes in the
surrounding environment. In particular, a neural
network trained to operate in a specific
environment can be easily retrained to deal with
minor changes in the operating environmental
conditions.
Properties and Capabilities of Neural
Networks
Moreover, when it is operating in a nonstationary
environment (i.e., one whose statistics change
with time), a neural network can be designed to
change its synaptic weights in real time. The
natural architecture of a neural network for
pattern classification, signal processing, and
control applications, coupled with the adaptive
capability of the network, make it an ideal tool for
use in adaptive pattern classification, adaptive
signal processing, and adaptive control.
Properties and Capabilities of
Neural Networks
As a general rule, it may be said that the more
adaptive we make a system in a properly
designed fashion, assuming the adaptive system
is stable, the more robust its performance will
likely be when the system is required to operate
in a nonstationary environment.
Properties and Capabilities of
Neural Networks
It should be emphasized, however, that
adaptivity does not always lead to
robustness; indeed, it may do the very
opposite. For example, an adaptive system
with short time constants may change
rapidly and therefore tend to respond to
spurious disturbances, causing a drastic
degradation in system performance.
Properties and Capabilities of
Neural Networks
To realize the full benefits of adaptivity, the
principal time constants of the system should be
long enough for the system to ignore spurious (L.
spurius, false) disturbances and yet short enough
to respond to meaningful changes in the
environment; the problem described here is
referred to as the stability-plasticity dilema
(Grossberg, 1988). Adaptivity (or “in situ,(L.)in
the original situation” training as it is sometimes
referred to) is an open research topic.
Properties and Capabilities of
Neural Networks
4. Evidential Response
In the context of pattern classification, a neural
network can be designed to provide information
not only about which particular pattern to select,
but also about the confidence in the decision
made. This latter information may be used to
reject ambiguous patterns, should they arise, and
thereby improve the classification performance of
the network.
Properties and Capabilities of
Neural Networks
5.
Contextual Information
(L. contextus,contexere-con-, texere, textum, to weave)
Knowledge is represented by the very structure and
activation state of a neural network.
Every neuron in the network is potentially affected by the
global activity of all other neurons in the network.
Consequently, contextual information is dealt with
naturally by a neural network.
Properties and Capabilities of
Neural Networks
6. Fault Tolerance
A neural network, implemented in hardware form, has
the potential to be inherently fault tolerant in the sense
that its performance is degraded gracefully under adverse
operating conditions (Bolt, 1992).
For example, if a neuron or its connecting links are
damaged, recall of a stored pattern is impaired in quality.
However, owing to the distributed nature of information
in the network, the damage has to be extensive before
the overall response of the network is degraded seriously.
Thus, in principle, a neural network exhibits a graceful
degradation in performance rather than catastrophic
failure.
Properties and Capabilities of
Neural Networks
7. VLSI Implementability
The massively parallel nature of a neural network makes it
potentially fast for the computation of certain tasks. This same
feature makes a neural network ideally suited for implementation
using very-Iarge-scale-integrated (VLSI) technology.
The particular virtue of VLSI is that it provides a means of
capturing truly complex behavior in a highly hierarchical fashion
(Mead and Conway, 1980), which makes it possible to use a neural
network as a tool for real-time applications involving pattern
recognition, signal processing, and control.
Properties and Capabilities of
Neural Networks
8. Uniformity of Analysis and Design. Basically, neural
networks enjoy universality as information processors.
We say this in the sense that the same notation is used in
all the domains involving the application of neural
networks. This feature manifests itself in different ways:
Neurons, in one form or another, represent an ingredient
common to all neural networks.
This commonality makes it possible to share theories
and learning algorithms in different applications of
neural networks.
Modular networks can be built through a seamless
integration of modules.
Properties and Capabilities of Neural
Networks
analysis: [Medieval Latin, from Greek analusis, a dissolving, from analūein, to
undo : ana-, throughout; see ana- + lūein, to loosen; see leu- in Indo-European
roots.]
(Download Now or Buy the Book) The American Heritage® Dictionary of the English
Language, Fourth Edition
Copyright © 2006 by Houghton Mifflin Company.
Published by Houghton Mifflin Company. All rights reserved.Online Etymology
Dictionary - Cite This Source - Share This
analysis
1581, "resolution of anything complex into simple elements" (opposite of
synthesis), from M.L. analysis, from Gk. analysis "a breaking up," from analyein
"unloose," from ana- "up, throughout" + lysis "a loosening" (see lose).
Psychological sense is from 1890. Phrase in the final (or last) analysis (1844),
translates Fr. en dernière analyse.
Properties and Capabilities of Neural
Networks
Design: 1548, from L. designare "mark out,
devise," from de- "out" + signare "to mark," from
signum "a mark, sign." Originally in Eng. with the
meaning now attached to designate (1646, from L.
designatus, pp. of designare); many modern uses
of design are metaphoric extensions. Designer
(adj.) in the fashion sense of "prestigious" is first
recorded 1966; designer drug is from 1983.
Designing "scheming" is from 1671. Designated
hitter introduced in American League baseball in
1973, soon giving wide figurative extension to
designated.
Properties and Capabilities of
Neural Networks
9. Neurobiological Analogy
The design of a neural network is motivated by
analogy with the brain, which is a living proof
that fault-tolerant parallel processing is not only
physically possible but also fast and powerful.
Neurobiologists look to (artificial) neural
networks as a research tool for the interpretation
of neurobiological phenomena.
Properties and Capabilities of
Neural Networks
For example, neural networks have been used to provide insight
on the development of premotor (relating to, or being the area of
the cortex of the frontal lobe lying immediately in front of the
motor area of the precentral gyrus(Any of the prominent, rounded,
elevated convolutions on the surfaces of the cerebral hemispheres.
[Latin gȳrus, circle; see gyre.] ) )circuits in the oculomotor
(1.Of or relating to movements of the eyeball: an oculomotor
muscle.
2.Of or relating to the oculomotor nerve.
[Latin oculus, eye; see okw- in Indo-European roots + motor.]
system (responsible for eye movements) and the manner in which
they process signals (Robinson, 1992). On the other hand,
engineers look to neurobiology for new ideas to solve problems
more complex than those based on conventional hard-wired
design techniques.
Properties and Capabilities of
Neural Networks
Here, for example, we may mention the development of
a model sonar receiver based on the bat (Simmons et aI.,
1992). The batinspired model consists of three stages:
(1) a front end that mimics the inner ear of the bat in
order to encode waveforms;
(2) a subsystem of delay lines that computes echo delays;
(3) a subsystem that computes the spectrum of echoes,
which is in turn used to estimate the time separation of
echoes from multiple target glints.
Properties and Capabilities of
Neural Networks
The motivation is to develop a new sonar receiver
that is superior to one designed by conventional
methods. The neurobiological analogy is also
useful in another important way: It provides a
hope and belief (and, to a certain extent, an
existence proof) that physical understanding of
neurobiological structures could indeed influence
the art of electronics and thus VLSI (Andreou,
1992).
Properties and Capabilities of
Neural Networks
With inspiration from neurobiological analogy in
mind, it seems appropriate that we take a brief
look at the structural levels of organization in the
brain.
Properties and Capabilities of
Neural Networks
1.2 Structural Levels of Organization in the
Brain
The human nervous system may be viewed
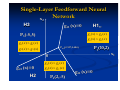
as a three-stage system,(Arbib, 1987).
Block-diagram representation of nervous system
Properties and Capabilities of
Neural Networks
Central to the system is the brain, represented by the
neural (nerve) net in this figure, which continually
receives information, perceives it, and makes
appropriate decisions. Two sets of arrows are shown in
this figure:
1 Those pointing from left to right indicate the forward
transmission of information-bearing signals through
the system.
2 The arrows pointing from right to left signify the
presence of feedback in the system.
Properties and Capabilities of
Neural Networks
The receptors in the figure convert stimuli from
the human body or the external environment into
electrical impulses that convey information to the
neural net (brain). The effectors, on the other
hand, convert electrical impulses generated by the
neural net into discernible responses as system
outputs. . In the brain there are both small-scale
and large-scale anatomical organizations, and
different functions take place at lower and higher
levels.
Properties and Capabilities of
Neural Networks
This figure shows a
hierarchy of interwoven
levels of organization that
has emerged from the
extensive work done on
the analysis of local
regions in the brain
(Churchland and
Sejnowski, 1992; Shepherd
and Koch, 1990).
Properties and Capabilities of
Neural Networks
Proceeding upward from synapses that represent
the most fundamental level and that depend on
molecules and ions for their action, we have
neural microcircuits dendritic trees, and then
neurons.
Properties and Capabilities of
Neural Networks
A neural microcircuit refers to an assembly
of synapses organized into patterns of
connectivity so as to produce a functional
operation of interest. A neural microcircuit
may be likened to a silicon chip made up of
an assembly of transistors.
Properties and Capabilities of
Neural Networks
The smallest size of microcircuits is measured in
micrometers (m), and their fastest speed of
operation is measured in milliseconds. The neural
microcircuits are grouped to form dendritic
subunits within the dendritic trees of individual
neurons. The whole neuron, about 100 m in size,
contains several dendritic subunits.
Properties and Capabilities of
Neural Networks
At the next level of complexity, we have local
circuits (about 1 mm in size) made up of
neurons with similar or different properties;
these neural assemblies perform operations
characteristic of a localized region in the
brain.
Properties and Capabilities of
Neural Networks
This is followed by interregional circuits made up
of pathways, columns, and topographic maps,
which involve multiple regions located in different
parts of the brain.
Properties and Capabilities of
Neural Networks
Topographic maps are organized to respond to
incoming sensory information. These maps are
often arranged in sheets, as in the superior
colliculus, where the visual, auditory, and
somatosensory maps are stacked in adjacent
layers in such a way that stimuli from
corresponding points in space lie above each
other. Finally, the topographic maps, and other
interregional circuits mediate specific types of
behavior in the central nervous system .
Properties and Capabilities of
Neural Networks
It is important to recognize that the
structural levels of organization described
herein are a unique characteristic of the
brain. They are nowhere to be found in a
digital computer, and we are nowhere close
to realizing them with artificial neural
networks. Nevertheless, we are inching our
way toward a hierarchy of computational
levels similar to that described in the last
figure.
Properties and Capabilities of
Neural Networks
The artificial neurons we use to build our
neural networks are truly primitive in
comparison to those found in the brain.
The neural networks we are presently able to
design are just as primitive compared to the
local circuits and the interregional circuits in
the brain.
Properties and Capabilities of
Neural Networks
What is really satisfying, however, is the
remarkable progress that we have made on
so many fronts during the past 20 years.
With the neurobiological analogy as the
source of inspiration, and the wealth of
theoretical and technological tools that we
are bringing together, it is for certain that in
another 10 years our understanding of
artificial neural networks will be much more
sophisticated than it is today.
Properties and Capabilities of
Neural Networks
Our primary interest here is confined to the study
of artificial neural networks from an engineering
perspective, to which we refer simply as neural
networks. We begin the study by describing the
models of (artificial) neurons
that form the basis of the neural networks
considered in these lectures.
Models of a Neuron
Models of a Neuron
A neuron is an information-processing unit that is
fundamental to the operation of a neural network.
The figure on the next slide shows the model for a
neuron.
Models of a Neuron
Nonlinear model of a neuron
Models of a Neuron
1. A set of synapses or connecting links, each
of which is characterized by a weight or
strength of its own. Specifically, a signal xj
at the input of synapse j connected to
neuron k is multiplied by the synaptic
weight wkj. It is important to make a note
of the manner in which the subscripts of
the synaptic weight wkj are written.
Models of a Neuron
The first subscript refers to the neuron in
question and the second subscript refers to
the input end of the synapse to which the
weight refers; the reverse of this notation is
also used in the literature.
The weight wkj is positive if the associated
synapse is excitatory; it is negative if the
synapse is inhibitory (Middle English
inhibiten, to forbid, from Latin inhibēre, inhibit, to restrain, forbid : in-, in; see in-2 + habēre, to
hold; see ghabh- in Indo-European roots.] )
Models of a Neuron
2.An adder for summing the input signals,
weighted by the respective synapses of
the neuron; the operations described
here constitute a linear combiner.
Models of a Neuron
3.An activation function for limiting the amplitude
of the output of a neuron. The activation function,
is also referred to in the literature as a squashing
function in that it squashes (limits) the permissible
amplitude range of the output signal to some finite
value. Typically, the normalized amplitude range
of the output of a neuron is written as the closed
unit interval [0,1] or alternatively [-1,1].
Models of a Neuron
4. The model of a neuron also includes an
externally applied threshold k that has the
effect of lowering the net input of the
activation function.
On the other hand, the net input of the
activation function may be increased by
employing a bias term rather than a
threshold; the bias is the negative of the
threshold.
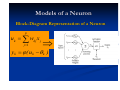
Models of a Neuron
In mathematical terms, we may describe neuron k by
writing the following pair of equations:
p
Mathematical Model
of a Neuron
uk wkj x j
j 1
yk ( uk k )
where xj’s are the input signals; wkj’s are the synaptic
weights of neuron k; uk is the linear combiner output;
k is the threshold; is the activation function;
and yk is the output signal of the neuron.
Models of a Neuron
Block-Diagram Representation of a Neuron
p
uk wkj x j
j 1
yk ( u k k )
Models of a Neuron
The use of threshold k
has the effect of
applying an affine transformation to the
output uk of the linear combiner in the
model of the figure, as shown by
vk u k k
Models of a Neuron
In particular, depending on
whether the threshold k is
positive or negative, the
relationship between the
effective internal activity level or
activation potential vk of neuron
k and the linear combiner
output uk is modified in the
manner illustrated in the figure.
Note that as a result of this
affine transformation, the graph
of vk versus uk no longer passes
through the origin.
Models of a Neuron
The threshold k is an external parameter
of artificial neuron k. We may account for its
presence as in the above equation.
Equivalently, we may formulate the
combination of the two equations as follows:
p
vk wkj x j
j 0
yk (vk )
Models of a Neuron
Here we have added a new synapse, whose input
is
x0 1
and whose weight is
wk 0 k
Models of a Neuron
We may therefore
reformulate the model
of neuron k as in the
figure, where the effect
of the threshold is
represented by doing
two things:
Models of a Neuron
(1) adding a new input signal fixed at -1, and
(2) adding a new synaptic weight equal to the
threshold k .
Alternatively, we may model the neuron as in
the following slide:
Y1
Models
of
a
Neuron
where the
combination of
fixed input
xo = + 1 and
weight wkO = bk
accounts for the
bias bk•
Although the
models of the
two figures are
different in
appearance,
they are
mathematically
equivalent.
Slayt 92
Y1
YTU; 15.03.2005
Models of a Neuron
Signal-Flow Graph Representation of a Neuron
uk
p
w
j 1
kj
xj
yk ( uk k )
Models of a Neuron
Signal-Flow Graph Representation of a Neuron
Two different types of links may be distinguished:
(a) Synaptic links, defined by a linear input-output
relation. Specifically, the node signal xj is
multiplied by the synaptic weight wkj to produce
the node signal vk .
(b) Activation links, defined in general by a
nonlinear input-output relation. This form of
relationship is the nonlinear activation function
given as
(.)
Models of a Neuron
The Activation Function
The activation function, denoted by
y (v )
defines the output y of a neuron in terms of the
activity level at its input v.
Models of a Neuron
We may identify three basic types of activation
functions:
Threshold Function
2. Piecewise-linear Function
3. Sigmoid Function
1.
Models of a Neuron
Threshold (hard limiter or binary activation )
Function (leading to discrete perceptron)
1.
(v )
1 1
(v) sgn(v)
2 2
1
0
(a) Unipolar
v
Models of a Neuron
(v )
(v) sgn(v)
1
v
00
0
-1
(b) Bipolar
Models of a Neuron
2. Piecewise-linear Function
(v )
1 1
1
1
(v ) v v
2 2
2
2
1
0.5
-0.5
0
0
0
(a) Unipolar
v
y ij (t ) f ( xij )
1
xij (t ) 1 x ij (t ) 1
2
Models of a Neuron
(v )
1
(v ) v 1 v 1
2
1
-1
0
1
-1
(b) Bipolar
v
Models of a Neuron
3. Sigmoid Function
(v )
1
0.5
(a) Unipolar
1
(v )
;a 0
av
1
e
v
Models of a Neuron
(v )
1
v
-1
(b) Bipolar
1 e av
2
=
-1 ; a 0
(v )
av
av
1 e
1 e
Models of Artificial Neural Networks
DEFINITION OF Neural Network
(Jacek M. Zurada, ARTIFICIAL NEURAL SYSTEMS, 1992, West Publishing Company)
A Neural Network is an interconnection of
neurons such that neuron outputs are
connected, through weights, to all other
neurons including themselves; both lagfree
and delay connections are allowed.
Models of Artificial Neural Networks
Neural Networks Viewed as Directed Graphs
1.
2.
Block-Diagram Representation (BDR)
Signal-Flow Graph Representation (SFGR)
These are obtained when BDR and SFGR for
the neurons are used.
Models of Artificial Neural Networks
An alternative definition of Neural Network
(Simon Haykin, NEURAL NETWORKS, 1994, Macmillan College Publishing Company)
A neural network is a directed graph (SFG) consisting of
nodes with interconnecting synaptic and activation
links, and which is characterized by four properties:
Each neuron is represented by a set of linear synaptic
links, an externally applied threshold, and a nonlinear
activation link. The threshold is represented by a
synaptic link with an input signal fixed at a value of -1.
Models of Artificial Neural Networks
2. The synaptic links of a neuron weight their
respective input signals.
3. The weighted sum of the input signals
defines the total internal activity level of
the neuron in question.
4. The activation link squashes the internal
activity level of the neuron to produce an
output that represents the output of the
neuron.
Network Architectures
In general, we may identify four different
classes of network architectures:
1. Single-Layer Feedforward Networks
2. Multilayer Feedforward Networks
3. Recurrent Networks
4. Lattice Structures
Network Architectures
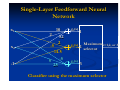
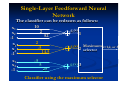
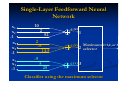
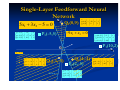
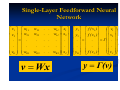
1.
Single-Layer Feedforward Networks
A layered neural network is a network of
neurons organized in the form of layers. In
the simplest form of a layered network, we
just have an input layer of source nodes that
projects onto an output layer of neurons
(computation nodes), but not vice versa.
Network Architectures
In other words, this network is strictly of a
feedforward type. It is illustrated on the
following slide for the case of four nodes in
both the input and output layers. Such a
network is called a single-layer network,
with the designation "single layer" referring
to the output layer of computation nodes
(neurons). In other words, we do not count
the input layer of source nodes, because no
computation is performed there.
Network Architectures
Network Architectures
2. Multilayer Feedforward Networks
The second class of a feedforward neural
network distinguishes itself by the presence
of one or more hidden layers, whose
computation nodes are correspondingly
called hidden neurons or hidden units. The
function of the hidden neurons is to
intervene between the external input and the
network output.
Network Architectures
Network Architectures
By adding one or more hidden layers, the network is
enabled to extract higher-order statistics, for (in a rather
loose sense) the network acquires a global perspective
despite its local connectivity by virtue of:
the extra set of synaptic connections
the extra dimension of neural interactions.
The ability of hidden neurons to extract higher-order
statistics is particularly valuable when the size of the
input layer is large.
Network Architectures
The source nodes in the input layer of the
network supply respective elements of the
activation pattern (input vector), which constitute
the input signals applied to the neurons
(computation nodes) in the second layer (i.e., the
first hidden layer). The output signals of the
second layer are used as inputs to the third layer,
and so on for the rest of the network.
Network Architectures
Typically, the neurons in each layer of the
network have as their inputs the output signals of
the preceding layer only.
The set of output signals of the neurons in the
output (final) layer of the network constitutes the
overall response of the network to the activation
pattern supplied by the source nodes in the input
(first) layer.
Network Architectures
This graph illustrates the
layout of a multilayer
feedforward neural
network for the case of a
single hidden layer. For
brevity this network is
referred to as a 10-4-2
network in that it has 10
source nodes, 4 hidden
neurons, and 2 output
neurons.
Network Architectures
As another example, a feedforward
network with p source nodes, h1
neurons in the first hidden layer, h2
neurons in the second layer, and q
neurons in the output layer, say, is
referred to as a p-h1-h2-q network.
Network Architectures
The neural network of
this figure is said to
be fully connected in
the sense that every
node in each layer of
the network is
connected to every
other node in the
adjacent forward
layer.
Network Architectures
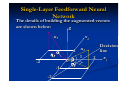
If, however, some of the communication links
(synaptic connections) are missing from the
network, we say that the network is partially
connected. A form of partially connected
multilayer feedforward network of particular
interest is a locally connected network. An
example of such a network with a single hidden
layer is presented on the next slide. Each neuron
in the hidden layer is connected to a local (partial)
set of source nodes that lies in the immediate
neighborhood.
Network Architectures
Such a set of localized
nodes feeding a neuron
is said to constitute the
receptive field of the
neuron.
Likewise, each neuron in
the output layer is
connected to a local set
Partially connected
of hidden neurons.
feedforward neural network
Network Architectures
3. Recurrent (Feedback or Dynamical)
Networks
A recurrent neural network
distinguishes itself from a feedforward
neural network in that it has at least
one feedback loop. For example, a
recurrent network may consist of a
single layer of neurons with each
neuron feeding its output signal back
to the inputs of all the other neurons,
as illustrated in the architectural
graph of the figure on the right. In the
structure depicted in this figure there
are no self-feedback loops in the
Recurrent network with no
network; self-feedback refers to a
situation where the output of a neuron self-feedback loops and no
is fedback to its own input.
hidden neurons
Network Architectures
The recurrent network
illustrated on the previous
slide also has no hidden
neurons. Here we illustrate
another class of recurrent
networks with hidden
neurons. The feedback
connections shown originate
from the hidden neurons as
well as the output neurons.
Recurrent network with
hidden neurons
Network Architectures
The presence of feedback loops, be it as in the
recurrent structure with or without hidden
neurons, has a profound impact on the learning
capability of the network, and on its
performance. Moreover, the feedback loops
involve the use of particular branches
composed of unit-delay elements (denoted by
z-1), which result in a nonlinear dynamical
behavior by virtue of the nonlinear nature of
the neurons.
Network Architectures
4. Lattice (Multicategory Perceptron)
Structures
A lattice consists of a one-dimensional,
two-dimensional, or higher-dimensional
array of neurons with a corresponding set
One dimensional lattice of 3 neurons
of source nodes that supply the input
signals to the array; the dimension of the
lattice refers to the number of the
dimensions of the space in which the
graph lies.
A lattice network is really a feedforward
network with the output neurons
arranged in rows and columns.
Two dimensional lattice of 3-by-3 neurons
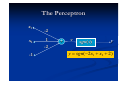
The Perceptron
The perceptron is the simplest
form of a neural network used
for the classification of a special
type of patterns said to be
linearly separable (i.e., patterns
that lie on opposite sides of a
hyperplane).
Basically, it consists of a single
neuron with adjustable synaptic
weights and threshold, as shown
in the figures.
The Perceptron
The algorithm used to adjust the free parameters of this
neural network first appeared in a learning procedure
developed by Rosenblatt (1958, 1962) for his perceptron
brain model. Indeed, Rosenblatt proved that if the
patterns (vectors) used to train the perceptron are drawn
from two linearly separable classes, then the perceptron
algorithm converges and positions the decision surface in
the form of a hyperplane between the two classes. The
proof of convergence of the algorithm is known as the
perceptron convergence theorem.
The Perceptron
The single-layer perceptron depicted has a single
neuron. Such a perceptron is limited to performing
pattern classification with only two classes.
By expanding the output (computation) layer of the
perceptron to include more than one neuron, we may
correspondingly form classification with more than two
classes. However, the classes would have to be linearly
separable for the perceptron to work properly.
The Perceptron
From this model we find that
the linear combiner output
(i.e., hard limiter input) is
p
v wkj x j
j 1
The purpose of the perceptron is to classify the set of
externally applied stimuli x1 ,x2,…., xp into one of two
classes, C1 or C2, say. The decision rule for the
classification is to assign the point represented by the
inputs x1 ,x2,…., xp to class C1, if the perceptron output y is
+ 1 and to class C2 if it is -1.
The Perceptron
To develop insight into the behavior of a pattern
classifier, it is customary to plot a map of the decision
regions in the p-dimensional signal space spanned by
the p input variables x1 ,x2,…., xp. In the case of an
elementary perceptron, there are two decision regions
separated by a hyperplane defined by
p
w
j 1
kj
xj 0
The Perceptron
This is illustrated here for the case of
two input variables xl and x2, for which
the decision boundary takes the form of
a straight line called the decision line. A
point (x1,x2) that lies above the decision
line is assigned to class C1, and a point
(x1,x2) that lies below the decision line
is assigned to class C2. Note also that
the effect of the threshold is merely to
shift the decision line away from the
origin. The synaptic weights w1 w2, ..,wp
of the perceptron can be fixed or
adapted on an iteration-by-iteration
basis. For the adaptation, we may use
an error-correction rule known as the
perceptron convergence algorithm.
The Perceptron
We find it more convenient to
work with the modified
signal
flow graph given here.
In this second model, which is
equivalent to that of the previous
figure, the threshold is treated as
a synaptic weight is connected
to a fixed input equal to -1. We may thus define the
(p + 1)-by-1 (augmented) input vector and the
corresponding (augmented) weight vector as:
x [ x1
x2 ... ... x p 1]t
w [ w1
w2 ... ... wp
]t
The Perceptron
Pattern Space
Any pattern can be represented by a point in
n-dimensinal Euclidean space En called the
pattern space. Points in that space corresponding to
members of the pattern set are n-tuple vectors x.
The Perceptron
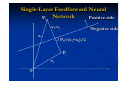
Example 1: Consider the six patterns in two dimensional
pattern space shown in the following figure.
x2
(0, 0)
(-0.5, -1)
(-1, -2)
(2,0)
x1
(1.5,-1)
(1, -2)
The Perceptron
Design a perceptron such that these are classified
according to their membership in sets as follows :
2
1.5
1
, , : class 1
1
2
0
0
0.5
1
, : class 2
,
1
2
0
The Perceptron
One possible decision line is given by x2= 2x1-2
which is drawn in the following figure.
x2
x = 2x -2
2
1
(0, 0)
(-0.5, -1)
(-1, -2)
(2,0)
x1
(1.5,-1)
(1, -2)
The Perceptron
One decision surface for this line is obtained as:
x3 2 x1 x2 2
x3 0 2 x1 x2 2 0 gives the points on the decision line
x3 0 2 x1 x2 2 0 gives the part of the surface above the decision line
x3 0 2 x1 x2 2 0 gives the part of the surface below the decision line
Such a pattern classification can be performed by
the following (discrete) perceptron (dichotomizer):
dichotomize: to divide or separate into two parts
dicha: in two; tomia: to cut
The Perceptron
x1
x2
-2
1
-2
-1
+
v
sgn(v)
y
y sgn(2 x1 x2 2)
Single-Layer Feedforward Neural
Network
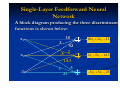
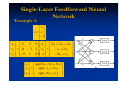
Example 2: Assume that a set of eight points,
P0, P1... , P7 , in three-dimensional space is available.
The set consists of all vertices of a three-dimensional
cube as follows:
{P0(-l, -1, -l), P1(-l, -1, l), P2(-1, 1, -1), P3(-1, 1, 1),
P4(1, -1, -l), P5(1, -1, 1), P6(1,1, -1), P7(1, 1, 1)}
Elements of this set need to be classified into two categories
The first category is defined as containing points with two
or more positive ones; the second category contains all the
remaining points that do not belong to the first category.
Single-Layer Feedforward Neural
Network
Classification of points P3, P5, P6, and P7 can be
based on the summation of coordinate values for
each point evaluated for category membership.
Notice that for each point Pi (x1, x2, x3) ,where
i = 0, ... , 7, the membership in the category can be
established by the following calculation:
1, then category 1
If sgn( x1 x2 x3 )
1, then category 2
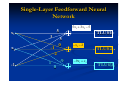
Single-Layer Feedforward Neural
Network
The neural network given below implements the
above expression:
Single-Layer Feedforward Neural
Network
The network above performs the
threedimensional Cartesian space partitioning
as illustrated below :
Single-Layer Feedforward Neural
Network
Discriminant Functions
In Example 1
x3 2 x1 x2 2
can be viewed as a Discriminant Function. We
may also write
g ( x1 , x2 ) 2 x1 x2 2
or
x1
g ( x ) 2 x1 x2 2 where x =
x2
Single-Layer Feedforward Neural
Network
g ( x1 , x2 ) 2 x1 x2 2
can also be viewed as the equation of a plane in
3-D Euclidean space.
On the other hand
g ( x1 , x2 ) 0 2 x1 x2 2 0
is the intersection line of the above plane with the
xy-plane.
Single-Layer Feedforward Neural
Network
Obviously:
g ( x ) 0 2 x1 x2 2 0 gives the points on the decision line
g ( x ) 0 2 x1 x2 2 0 gives the points on the plane above the decision line
g ( x ) 0 2 x1 x2 2 0 gives the points on the plane below the decision line
Single-Layer Feedforward Neural
Network
Since on the decision line we have
g ( x1 , x2 ) 0
we can write
g ( x1 , x2 )
g ( x1 , x2 )
dg ( x1 , x2 )
dx1
dx2 0
x1
x2
where dx1 and dx2 are the increments given to
x1 and x2 on the decision line.
Single-Layer Feedforward Neural
Network
Now defining
where
g ( x1 , x2 )
x
dx1
1
and dr
g ( x1 , x2 )
g ( x1 , x2 )
dx2
x
2
g and dr
are known to be the gradient vector (or normal
vector) and the tangent vector, respectively,
Single-Layer Feedforward Neural
Network
The gradient vector points toward the positive side
of the decision line. However, there are two normal
vectors, one pointing toward the positive side, 1,
and the other toward the negative side, 2 =-1.
For the above example the gradient and normal
vectors are given by:
g ( x1 , x2 )
x
2
2
2
1
, 1 g ( x1 , x2 ) ,2
g ( x1 , x2 )
g ( x1 , x2 ) 1
1
1
x
2
Single-Layer Feedforward Neural
Network
In fact 2 is obtained from
g ( x1 , x2 ) 0
Note that 1 and 2 are the projections of the
normal vectors on the x-y plane of two intersecting
planes whose intersection line is given by
g ( x1 , x2 ) 0
Single-Layer Feedforward Neural
Network
Although 1 and 2 are unique, there are infinetely
many plane pairs whose intersection line is given
by
g ( x1 , x2 ) 0
Plane pairs can be built by appropriately
augementing the 2-D normal vectors 1 and 2
to 3-D normal vectors which will be the normal
vectors of the two intersecting planes.
Single-Layer Feedforward Neural
Network
The 2-D normal vectors are plane vectors given in
the x-y plane.
2
2
1 ,2
1
1
These can be augmented to 3-D by adding a third
component, say 2, yielding
2
2
n1 1 , n2 1
2
2
Single-Layer Feedforward Neural
Network
The details of building the augmented vectors
are shown below:
g
n1
-2
-1
-2
x2
Decision
line
n
1 2
0
1
2
x1
Single-Layer Feedforward Neural
Network
Note that 1 and 2 are the normal vectors of the
plane that is perpendicular to the x-y plane and
intersects the x-y plane at the decision line.
On the other hand the vectors n1 and n2 are the
normal vectors of the planes obtained by rotating
the above perpendicular plane around the decision
line by and , respectively.
Single-Layer Feedforward Neural
Network
We can now determine the equations for the these
planes by using the normal vector-point form of
plane equation given as:
t
n ( x x0 ) 0
where:
•n is the normal vector of the plane,
•x is the vector connecting any point on the plane
to the origin,
•x0 is the vector connecting a fixed point on the
plane to the origin.
Single-Layer Feedforward Neural
Network
This means that x-x0 represents the vector
connecting all possible points x on the plane
to fixed point x0 on the same plane. That is x-x0
is a vector that lies on the plane.
Now let us find the plane equations for the two
normal vectors found above.
Single-Layer Feedforward Neural
Network
Let x0 be the point (1,0,0) on the decision line.
We can write:
x1 1
2
1
For n1 1 2 1 2 x2 0 0 g1 x1 x2 1
2
2
g1 0
x1 1
2
1
For n2 1 2 1 2 x2 0 0 g 2 x1 x2 1
2
2
g 2 0
Single-Layer Feedforward Neural
Network
Because of the way g1(x) and g2(x) are built we can
state the following:
g1 ( x) g 2 ( x) 0 on the positive side of the decision line
g 2 ( x) g1 ( x) 0 on the negative side of the decision line
2
2
1
1
For n1 1 g1 x1 x2 1 For n2 1 g 2 x1 x2 1
2
2
2
2
Single-Layer Feedforward Neural
Network
g
n2
n1
g2
Decision
Decisio
line
g1
x1
Decision
line
x2
Single-Layer Feedforward Neural
Network
Now we can compute g1(x) and g2(x) for the selected
patterns in Example 1.
Class 1
Class 2
(2,0)
(1.5,-1)
(1,-2)
(0,0)
(-0.5,1)
(-1,-2)
g1-g2>0
g1-g2>0
g1-g2>0
g2-g1>0
g2-g1>0
g2-g1>0
Single-Layer Feedforward Neural
Network
Henceforth, such gi(x) functions will be called
Discriminant Functions. We can conclude that:
g1 ( x) g 2 ( x) for the patterns in Class 1
g 2 ( x) g1 ( x) for the patterns in Class 2
Single-Layer Feedforward Neural
Network
Minimum Distance Classification
The classification of two clusters is carried out in
such a way that the boundary of these two clusters
is drawn as a line perpendicular to and passing
through the midpoint of the line connecting the
center points of two clusters . Therefore the
boundary line is the perpendicular bisector of a
connecting line.
Single-Layer Feedforward Neural
Pi Network
Positive side
xi-xj
xi
Negative side
P0=(xi+xj)/2
Pj
xj
0
Single-Layer Feedforward Neural
Network
Now we will derive the equation of the boundary line.
Let the vector x and x0 represent any point on this and
the point P0, respectively. Then the following must hold:
( xi x j ) ( x x 0 ) 0
t
which can be written in the form
1
( xi x j ) ( x ( xi x j )) 0
2
t
Single-Layer Feedforward Neural
Network
and
1
t
( xi x j ) x ( xi x j ) ( xi x j ) 0
2
t
or
2
1
2
( xi x j ) x ( xi x j ) 0
2
t
Single-Layer Feedforward Neural
Network
Now defining
1
gij ( x ) ( xi x j ) x ( xi
2
t
2
2
xj )
We have already seen that the boundary (decision)
line can be taken as the intersection of two planes
gi and gj .
Single-Layer Feedforward Neural
Network
Therefore
gij ( x ) gi ( x ) g j ( x )
where we have called gi (x) discriminant functions
and shown that they are associated with plane
equations.
Single-Layer Feedforward Neural
Network
Now using the two equations above we obtain
2
1
2
( xi x j ) x ( xi x j ) gi ( x ) g j ( x )
2
t
which can be used to make the following
identification:
1
gi ( x ) xi x xi
2
t
2
1
g j ( x) x j x x j
2
t
2
Single-Layer Feedforward Neural
Network
gi (x) can also be expressed as:
gi ( x ) wi x wi ,n1
t
Therefore we can make the identification:
wi = x i
1
wi ,n1 xi
2
2
Single-Layer Feedforward Neural
Network
An alternative approach towards the construction
of discriminant functions may be taken as follows:
Let us assume that a minimum–distance
classification is requried to classify patterns into
R categories. Each of the classes is represented by
its center point Pi , i=1,2,…..,R. The Euclidean
distance between an input pattern x and the point
Pi is given by the norm of the vector x-xi as:
x xi ( x xi ) ( x xi )
t
Single-Layer Feedforward Neural
Network
A minimum–distance classifier computes the distance
from a pattern of unknown classification to each of the
center points Pi . Then the category number of the point
that yields the minimum distance is assigned to the
unknown pattern.
Squaring the above equation yields
x xi
2
1 t
x x - 2x x + x xi = x x - 2(x x - xi xi ) > 0
2
t
t
i
t
i
t
t
i
Single-Layer Feedforward Neural
Network
Since xxt is independent of i, this term is constant
with respect to the categories. Therefore, in order
to minimize the distance
x xi
we need to maximize
1 t
gi (x) = x x - xi xi
2
t
i
which is called a discriminant function.
Single-Layer Feedforward Neural
Network
Example 3: A linear minimum-distance classifier
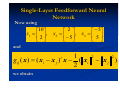
will be designed for the three points given as:
10
2
5
x1 , x2 , x3
2
5
5
It is also assumed that the index of each point
(pattern)corresponds to its class number.
The three points and the connecting lines
constitute a triangle which is shown on the
next slide:
Single-Layer Feedforward Neural
Network
x2
P3(-5,5)
P1(10,2)
0
P2(2,-5)
x1
Single-Layer Feedforward Neural
Network
Now let us draw the circle passing through all three
vertices of the triangle, the circumcircle. We can
conclude that each boundary is a perpendicular
bisector of the triangle. A perpendicular bisector of a
triangle is a straight line passing through the
midpoint of a side and being perpendicular to it, i.e.
forming a right angle with it. The three
perpendicular bisectors meet at a single point, the
triangle's circumcenter; this point is the center of the
circumcircle.
Single-Layer Feedforward Neural
Network
x2
P3(-5,5)
0
P2(2,-5)
P1(10,2)
x1
Single-Layer Feedforward Neural
Network
Now using
10
2
5
x1 , x2 , x3
2
5
5
and
1
t
gij ( x ) ( xi x j ) x ( xi
2
we obtain
2
2
xj )
Single-Layer Feedforward Neural
Network
1
2
2
g12 ( x ) ( x1 x2 ) x ( x1 x2 )
2
t
t
10 2 x1 1
[(100 4) (4 25)]
2 5 x2 2
8 x1 7 x2 37.5
Single-Layer Feedforward Neural
Network
1
2
2
g13 ( x ) ( x1 x3 ) x ( x1 x3 )
2
t
t
10 5
2 5
15 x1 3 x2 27
x1 1
x 2 [(100 4) (25 25)]
2
Single-Layer Feedforward Neural
Network
1
2
2
g 23 ( x ) ( x2 x3 ) x ( x2 x3 )
2
t
t
2 5 x1 1
[(4 25) (25 25)]
5 5 x2 2
7 x1 10 x2 10.5
Single-Layer Feedforward Neural
Network
Now using
wi = x i
1
wi ,n1 xi
2
2
we obtain
10
2
5
w1 2 ; w2 5 ; w3 5 ;
-52
-14.5
-25
Single-Layer Feedforward Neural
Network
and using
gi ( x ) wi x wi ,n1
t
we obtain
g1 ( x ) 10 x1 2 x2 52
g 2 ( x ) 2 x1 5 x2 14.5
g3 ( x ) 5 x1 5 x2 25
Single-Layer Feedforward Neural
Network
A block diagram producing the three discriminant
functions is shown below:
x1
x2
-1
10
2
52
2
-5
14.5
5
-5
25
10 x1 2 x2 52
2 x1 5 x2 14.5
5 x1 5 x2 25
Single-Layer Feedforward Neural
Network
The discriminant values for the three patterns
P1(10,2), P2(2,-5) and P3(-5,5) are shown in the
table below:
Input
g1(x)=10x1+2x2-52
Class 1
[10 2]t
52
Class 2
[2 -5]t
-42
Class 3
[-5 5]t
-92
g2(x)= 2x1-5x2-14.5
-4.5
14.5
-49.5
g3(x)=-5x1+5x2-25
-65
-60
25
Discriminant
Single-Layer Feedforward Neural
Network
As required by the definition of the discriminant
function, the responses on the diagonal are the
largest in each column. It will be shown later that
the same is true for any three points P1,P2 ,P3 taken
from the three decision regions H1,, H2, H3 provided
that the decision regions are determined as shown
above. Therefore using a maximum selector at the
output will provide the required function from the
network.
Single-Layer Feedforward Neural
Network
Using the same network with TLUs (bipolar
activation functions) will result in the outputs
given in the table below:
Input
Class 1
[10 2]t
sgn(g1(x)=5x1+3x2-5)
1
Class 2
[2 -5]t
-1
Class 3
[-5 5]t
-1
sgn(g2(x)= -x2-2)
-1
1
-1
sgn(g3(x)=-9x1+x2)
-1
-1
1
Single-Layer Feedforward Neural
Network
The diagonal entries=1
The offdiagonal entries=-1
However, as the next example will demonstrate
this is not true for any three points P1,P2 ,P3 taken
from the three decision regions H1, H2, H3.
Single-Layer Feedforward Neural
Network
The response of the same network to the patterns
Q1(5,0), Q2(0,1) and Q3(-4,0) are shown in the table below:
Input
Discriminant
g1(x)=10x1+2x2-52
Class 1
[5 0]t
-2
Class 2
[0 1]t
-50
Class 3
[-4 0]t
-92
g2(x)= 2x1-5x2-14.5
-4.5
-19.5
-22.5
g3(x)=-5x1+5x2-25
-50
-20
-5
Single-Layer Feedforward Neural
Network
The responses on the diagonal are still the largest
in each column. However, using the same network
with TLUs (bipolar activation functions) will result
in the outputs given in the table on the next slide:
Single-Layer Feedforward Neural
Network
Input
sgn(g1(x)=10x1+2x2-52)
Class 1
[5 0]t
-1
Class 2
[0 1]t
-1
Class 3
[-4 0]t
-1
sgn(g2(x)= 2x1-5x2-14.5)
-1
-1
-1
sgn(g3(x)=-5x1+5x2-25)
-1
-1
-1
Discriminant
Single-Layer Feedforward Neural
Network
It is therefore impossible to use TLUs once the
decision lines are calculated using the
minimum-distance calssification procedure.
The only way out is using a maximum selector.
The explanation of the responses on the diagonal
being the largest in each column will now be made
in detail.
Single-Layer Feedforward Neural
Network
The discriminant functions determine the plane
equations
g1 10 x1 2 x2 52 0
g 2 2 x1 5 x2 14.5 0
g3 5 x1 5 x2 25 0
Single-Layer Feedforward Neural
Network
These planes are shown on the next slide.
It is easily seen that:
For any point in H1 : g1(x)>g2(x) and g1(x)>g3(x)
For any point in H2 : g2(x)>g1(x) and g2(x)>g3(x)
For any point in H3 : g3(x)>g1(x) and g3(x)>g2(x)
Single-Layer Feedforward Neural
Network
100
50
0
gi
-50
-100
-150
-200
10
5
0
-5
x2
-10
-10
0
-5
x1
5
10
Single-Layer Feedforward Neural
Network
The decision regions H1,H2, H3 are projections of
the planes g1,g2 and g3, respectively, on the x1-x2
plane and the decision lines are the projections of
the intersection lines of the planes gi on the x1-x2
plane which are shown on the next slide.
Single-Layer Feedforward Neural
Network
x
2
H3
g13 (x)=0
H1,,
g1 ( x) g 2 ( x)
P3(-5,5)
g1 ( x) g3 ( x)
g3 ( x) g1 ( x)
P123(2.337,2.686)
g3 ( x) g 2 ( x)
0
g 2 ( x) g1 ( x)
g23 (x)=0
H2
g 2 ( x) g3 ( x)
P2(2,-5)
g12 (x)=0
P1(10,2)
x1
Single-Layer Feedforward Neural
Network
A MATLAB plot of the projections of the
intersection lines of the planes gi are shown
on the next slide
Single-Layer Feedforward Neural
Network
30
20
10
0
-10
-20
-30
-30
-20
-10
0
10
20
30
Single-Layer Feedforward Neural
Network
The projections of the intersection lines of the
planes gi on the x1-x2 plane are shown to be given
by the following line equations:
g12 ( x ) 8 x1 7 x2 37.5 0
g13 ( x ) 15 x1 3 x2 27 0
g 23 ( x ) 7 x1 10 x2 10.5 0
The previous slide shows the segments that can
be seen from the top.
Single-Layer Feedforward Neural
Network
The continuation of the line g12=0 remains
underneath the plane g3.
The continuation of the line g23=0 remains
underneath the plane g1.
The continuation of the line g13=0 remains
underneath the plane g2.
Single-Layer Feedforward Neural
Network
A classifier using a maximum selector is shown on
the next slide. The maximum selector selects the
maximum discriminant and responds with the
number of the discriminant having the largest
value.
Single-Layer Feedforward Neural
Network
x1
x2
-1
10
g1(x)
2
52
2
-5
14.5
5
-5
25
1
g2(x)
Maximum i=1,2, or 3
2 selector
g3(x)
3
Classifier using the maximum selector
Single-Layer Feedforward Neural
Network
The classifier can be redrawn as follows:
10
x1
g1(x)
2
x2
1
52
-1
2
x1
g2(x) Maximum i=1,2, or 3
5
2 selector
x2
14.5
-1
-5
x1
g3(x)
x2
5
3
25
-1
Classifier using the maximum selector
Single-Layer Feedforward Neural
Network
x1
x2
-1
x1
x2
-1
10
x1
x2
-1
-5
2
g1(x)
52
2
-5
g2(x)
Maximum i=1,2, or 3
2 selector
g3(x)
3
14.5
5
25
1
Classifier using the maximum selector
Single-Layer Feedforward Neural
Network
In the above we have designed a classifier which was
based on the minimumdistance classification for known
clusters and derived the network with three perceptrons
from the discriminant functions which were interpreted
as plane equations. Instead, now let us consider the
network on the next slide which is obtained as a result of
training a network with three perceptrons using the same input
patterns P1(10,2), P2(2,-5) and P3(-5,5) as in the previous network .
Single-Layer Feedforward Neural
Network
x1
x2
-1
5 x1 3 x2 5
5
TLU#1
3
5
0
-1
2
1
-9
0
x2 2
9x1 x2
TLU#2
TLU#3
Single-Layer Feedforward Neural
Network
In fact gi(x)=0 define the intersection of gi planes
with x1-x2 plane. Therefore the TLU divides the gi
planes into two regions:
(1)the upper-half plane which is above x1-x2 plane
and
(1)the lower-half plane which is below x1-x2 plane.
Single-Layer Feedforward Neural
Network
The decision lines are obtained by setting gi(x)=0
5 x1 3x2 5 0
x2 2 0
9 x1 x2 0
which are given on the next slide. The shaded
areas are indecision regions which will become
clear in the following discussion.
Single-Layer Feedforward Neural
Network
5 x1 3 x2 5 0
g1 (5,5) 15 1
g (5,5) 7 1
2
g 2 (5,5) 50 1
x2
Q1(0,9)
g1 (0,9) 22 1
g (0,9) 29 1
2
g 2 (0,9) 9 1
9 x1 x2 0
P3(-5,5)
P1(10,2)
x1
0
x2 2 0
g1 (1, 3) 19 1
g (1, 3) 1 1
2
g 2 (1, 3) 6 1
g1 (10, 2) 51 1
g (10, 2) 4 1
2
g 2 (10, 2) 88 1
Q2(4,-4)
Q3(-1,-3)
P2(2,-5)
g1 (2, 5) 10 1
g (2, 5) 3 1
2
g 2 (2, 5) 23 1
g1 (4, 4) 3 1
g (4, 4) 2 1
2
g 2 (4, 4) 40 1
Single-Layer Feedforward Neural
Network
The discriminant values g1(x), g2(x), g3(x) for
the same three patterns P1(10,2), P2(2,-5) and
P3(-5,5) are shown in the table below:
Input
Class 1
[10 2]t
51
Class 2
[2 -5]t
-10
Class 3
[-5 5]t
-15
g2(x)= -x2-2
-4
3
-7
g3(x)=-9x1+x2
-88
-23
50
Discriminant
g1(x)=5x1+3x2-5
Single-Layer Feedforward Neural
Network
The outputs of the network with three discrete
perceptrons are shown in the table below:
Input
Class 1
[10 2]t
1
Class 2
[2 -5]t
-1
Class 3
[-5 5]t
-1
sgn(g2(x)= -x2-2)
-1
1
-1
sgn(g3(x)=-9x1+x2)
-1
-1
1
sgn(g1(x)=5x1+3x2-5)
Single-Layer Feedforward Neural
Network
The table on the previous slide shows that the new
discriminant functions
g1 ( x ) 5 x1 3 x2 5
g 2 ( x ) x2 2
g3 ( x ) 9 x1 x2
classify the paterns P1(10,2), P2(2,-5) and P3(-5,5)
in the same way as the discriminant functions
g1 ( x ) 10 x1 2 x2 52
g 2 ( x ) 2 x1 5 x2 14.5
g3 ( x ) 5 x1 5 x2 25
Single-Layer Feedforward Neural
Network
Conclusion:
The network, which is obtained through the
perceptron learning algorithm, and the network
obtained using the maximum-distance classification
procedure have classified the three points
P1(10,2), P2(2,-5) and P3(-5,5) in exactly the same
way, i.e.,
P1 (10,2) class 1
P2 (2,-5) class 2
P3 (-5,5) class 3
Single-Layer Feedforward Neural
Network
Now consider the patterns Q1(0,9), Q2(4,-4)
and Q3(-1,-3) which fall into shaded areas.
The discriminant values for these patterns are
shown in the table on the next slide:
Single-Layer Feedforward Neural
Network
Input
[0 9]t
[4 -4]t
[-1 -3]t
g1(x)=5x1+3x2-5
22
3
-19
g2(x)= -x2-2
-29
2
1
9
-40
6
Discriminant
g3(x)=-9x1+x2
Single-Layer Feedforward Neural
Network
Since
g1 (0,9) g3 (0,9), g 2 (0,9)
g3 ( 1, 3)>g 2 (1, 3), g1 (1, 3)
g1 (4,-4)>g 2 (4,-4),g3 (4,-4)
if we use a maximum selector instead of the three
TLUs the network can decide that
Q1 (0,9) and Q 2 (4,-4) class 1
Q3 (1, 3) class 3
Single-Layer Feedforward Neural
Network
On the other hand, if we use TLUs we would
obtain the outputs in the following table:
Input
[0 9]t
[4 -4]t
[-1 -3]t
g1(x)=5x1+3x2-5
1
1
-1
g2(x)= -x2-2
-1
1
1
g3(x)=-9x1+x2
1
-1
1
Discriminant
Single-Layer Feedforward Neural
Network
In order to make a classification we should have a
column with one 1 and two -1s. Therefore
according to the table obtained non of the three
patterns Q1(0,9), Q2(4,-4) and Q3(-1,-3) could be
classified into any class. Therefore according to
the network with TLUs the shaded areas will be
called indecision regions.
Single-Layer Feedforward Neural
Network
Now let us consider the planes defined by
g1 5 x1 3 x2 5
g 2 x2 2
g3 9 x1 x2
which are plotted on the next slide:
Single-Layer Feedforward Neural
Network
100
50
gi
0
-50
-100
10
0
x2
-10
-10
-8
-6
-4
-2
x1
0
2
4
6
8
10
Single-Layer Feedforward Neural
Network
The projections of the intersection lines of the
planes gi(x) on the x1-x2 plane are given by
g12 : 5 x1 4 x2 3 0
g 23 : 9 x1 2 x2 2 0
g13 : 14 x1 2 x2 5 0
The segments that can be seen from the top are
plotted on the next slide.
Single-Layer Feedforward Neural
Network
15
10
5
0
-5
-10
-15
-10
-5
0
5
10
15
20
Single-Layer Feedforward Neural
Network
The continuation of the line g12=0 remains
underneath the plane g3.
The continuation of the line g23=0 remains
underneath the plane g1.
The continuation of the line g13=0 remains
underneath the plane g2.
Single-Layer Feedforward Neural
Network
x1
x2
w11
v1
wk1
v2
wK1
wK2
wkj vk
xj
xn
Input nodes
wmn
vm
y1
1
Neurons
2
y2
k
yk
K
ym
Output nodes
Single-Layer Feedforward Neural
Network
v1 w11 x1 w12 x2 ......... w1 j x j ...... w1J xJ
y1 f ( v1 )
v2 w21 x1 w22 x2 ......... w2 j x j ...... w2 J xJ
y2 f ( v2 )
vk wk1 x1 wk 2 x2 ......... wkj x j ...... wkJ xJ
yk f ( vk )
vK wK 1 x1 wK 2 x2 ......... wKj x j ...... wKJ xJ
y K f ( vK )
Single-Layer Feedforward Neural
Network
v1 w11
v w
2 21
. .
. .
vK wK 1
w12
w22
.
.
wK 2
. . w1J x1
. . w1J x2
. .
. .
. .
. .
. . wKJ xJ
v Wx
v1
y1 f ( v1 )
y f ( v )
v2
2
2
. . Γ .
.
. .
yK f ( vJ )
v J
y Γ(v)
Single-Layer Feedforward Neural
Network
y1 f (.)
y 0
2
. .
. .
yK 0
0 . .
f (.) . .
.
. .
.
0
. .
. .
v1
v
2
.
. .
f (.) vJ
0
0
.
y Γ[Wx]
Single-Layer Feedforward Neural
Network
Example 1:
x1
x x2
1
v1 5 3 5 x1 5 x1 3 x2 5 x3
v 0 1 2 x x 2 x
2
3
2
2
v3 9 1 0 1 9 x1 x2
y1 sgn(5 x1 3x2 5 x3 )
y sgn( x 2 x )
2
3
2
y3 sgn(9 x1 x2 )
Two-Layer Feedforward Neural
Network
Example 1: Design a neural network such that the network
maps the shaded region of plane x1, x2 into y = 1, and it
maps its complement into y = -1, where y is the output of the
neural network. In summary, the network will provide the
mapping of the entire x1, x2 plane into one of the two points
±1 on the real number axis.
Two-Layer Feedforward Neural
Network
Solution: The inputs to the neural network will
be x1, x2 and the threshold value -1. Thus the
input vector is given as:
x1
x x2
1
Two-Layer Feedforward Neural
Network
The boundaries of the shaded region are given
by the equations:
x1 1 0
x1 2 0
x2 0
x2 3 0
Two-Layer Feedforward Neural
Network
The shaded region satisfies the inequalities:
x1 1
x1 1 0
x1 2
x1 2 0
x2 0
x2 3
or
x2 0
x2 3 0
Two-Layer Feedforward Neural
Network
These inequalities may be implemented using
four neurons:
Two-Layer Feedforward Neural
Network
The equations for the first layer are obtained as:
v1 1 0 1
v 1 0 2 x1
2
x2
v3 0 1 0
1
v4 0 1 3
y sgn( x1 1) sgn( x1 2) sgn( x2 ) sgn( x2 3)
where binary (threshold or hard limiter )activation
function, i.e., discrete perceptron is used.
t
Two-Layer Feedforward Neural
Network
Let us discuss the mapping performed by the first
layer. Note that each of the neurons 1 through 4
divides the plane xl ,x2 into two half-planes.
The half-planes where the neurons' responses are
positive (+ 1) have been marked with arrows pointing
toward the positive response half plane.
The response of the. second layer can be easily
obtained as
y sgn( y1 y2 y3 y4 3.5)
Two-Layer Feedforward Neural
Network
The resultant neural network
The Perceptron Training Algorithm
For the development of the perceptron
learning algorithm for a single-layer
perceptron, we find it more convenient
to work with the modified
signal-flow graph model given here. In this second model,
which is equivalent to that of the previous figure, the threshold
is treated as a synaptic weight connected to a fixed input
equal to -1. We may thus define the (p + 1)-by-1 input vector and
the corresponding weight vector as:
x [ x1
x2 ... ... xn 1]t
w [ w1
w2 ... ... wn
]t
The Perceptron Training Algorithm
These vectors are respectively called the augmented input vector
and the augmented weight vector.
For fixed n, the equation wtx = 0, plotted in
p-dimensional space with coordinates xl; xz, ... , xp, defines a
hyperplane as the decision surface between two different classes of
inputs.
Suppose then the input variables of the single-layer perceptron
originate from two linearly separable classes that fall on the
opposite sides of some hyperplane. Let Xl be the subset of training
vectors xl(1), xl(2), ... that belong to class C1, and let X2 be the
subset of training vectors x2(1), x2(2), ...
that belong to class C2. The union of Xl and X2 is the complete
training set X.
The Perceptron Training Algorithm
Given the sets of vectors
X
and
X
to
train
the
classifier,
l
2
the training process involves the adjustment of the
weight vector w in such a way that the two classes Cl and
C2 are separable.
These two classes are said to be linearly separable if a
realizable setting of the weight vector w exists.
Conversely, if the two classes Cl and C2 are known to be
linearly separable, then there exists a weight vector w
such that we may state:
The Perceptron Training Algorithm
w x - 0
for every input vector x belonging to class C1
w x0
for every input vector x belonging to class C2
t
t
The Perceptron Training Algorithm
Given the subsets of training
vectors X1 and X2,
the training problem for the elementary ·perceptron
is then to find a weight vector w such that the two
inequalities above are satisfied.
However, until this is achieved in the itermediate steps
we will have
wx
- 0
for some input vectors x belonging to class C2
w x0
for some input vector x belonging to class C1
t
t
The Perceptron Training Algorithm
In the former case therefore
wt x will
be reduced until wt x 0 is achieved,
and in the latter case wt x will be
increased until wt x 0 is reached.
Here we will begin to examine neural
network classifiers that derive their
weights during the learning cycle.
The Perceptron Training Algorithm
• The sample pattern vectors x1 , x2, ... , xp, called
the training sequence, are presented to the
machine along with the correct response.
• The response is provided by the teacher and
specifies the classification information 'for
each mput vector. The classifier modifies its
parameters by means of iterative, supervised
learning.
The Perceptron Training Algorithm
The network learns from 'experience
by comparing the targeted correct
response with the actual response.
The classifier structure is usually
adjusted after each incorrect response
based on the error value generated.
The Perceptron Training Algorithm
Let us now look again at the dichotomizer
introduced and defined earlier.
We will develop a supervised training procedure
for this two-class linear classifier.
Assuming that the desired response is provided,
the error signal is computed.
The error information can be used to adapt the
weights of the discrete perceptron.
The Perceptron Training Algorithm
First we examine the geometrical conditions in
the augmented weight space.
This will make it possible to devise a
meaningful training procedure for the
dichotomizer under consideration.
The decision surface equation in n+1
dimensional augmented pattern space is
w x0
t
The Perceptron Training Algorithm
When the above equation is considered in the
pattern space then it is written for fixed weights
w(1), w(2),……….,w(k). Therefore the variables
of the function f(wt(i )x) are x1, x2,……….,xn+1 ,
the components of the pattern vector.
The Perceptron Training Algorithm
x2
f(wt(i )x)=0
w (i )
x1
The normal vector w(i ) (weight wector) points
toward the side of the pattern space for which
wt(i )x > 0, called the positive side.
The Perceptron Training Algorithm
When the above equation is considered in the
weight space then it is written for fixed patterns
x(1), x(2),……….,x(p). Therefore the variables of
the function f(wtx(i)) are w1, w2,……….,wn+1 , the
components of the weight vector.
The Perceptron Training Algorithm
w2
f(wtx(i))=0
w1
x ( i)
The normal vector x(i) (pattern vector) points
toward the side of the weight space for which
wtx(i) > 0, called the positive side.
The Perceptron Training Algorithm
∇
f ( w t x (i ))
f ( w1 , w2 ,....., wn1 )
w1
x1 (i )
f ( w1 , w2 ,....., wn1 )
x2 (i )
w2
x( i )
f ( w1 , w2 ,....., wn1 )
xn1 (i )
f ( w1 , w2 ,....., wn1 )
wn1
In further discussion it will be understood that the
normal vector will always point toward the side of
the space for which wtx> 0, called the positive side,
or semispace, of the hyperplane.
The Perceptron Training Algorithm
Decision hyperplane in augmented weight space
for a five pattern set from two classes
The Perceptron Training Algorithm
that the vectors x(i) points toward the
positive side of the decision hyperplanes
wtx(i)= 0.
Note
By labeling each decision boundary in the
augmented weight space with an arrow
pointing into the positive half-plane, we can
easily find a region in the weight space that
satisfies the linearly separable classification.
The Perceptron Training Algorithm
To find the solution for weights, we will
look for the intersection of the positive
decision regions due to the prototypes
of class 1·and of the negative decision
regions due to the prototypes of class 2.
The Perceptron Training Algorithm
Inspection
of the figure reveals that the
intersection of the sets of weights
yielding all five correct classifications
of depicted patterns is in the shaded
region of the second quadrant as shown
in the figure above.
The Perceptron Training Algorithm
Let us now attempt to arrive iteratively
at the weight vector w located in the
shaded weight solution area.
To accomplish this, the weights need
to be adjusted from the initial value
located anywhere in the weight space.
The Perceptron Training Algorithm
This assumption is due to our ignorance of
the weight solution region as well as weight
initialization.
The adjustment discussed, or network
training, is based on an error-correction
scheme.
The Perceptron Training Algorithm
At this point we will introduce the Perceptron
Learning (Traning) Rule (Algorithm).
The perceptron learning rule is of central
importance for supervised learning of neural
networks.
The weights are initialized at any values in this
method
The Perceptron Training Algorithm
A neuron is considered to be an adaptive
element. Its weights are modifiable
depending on the input signal it receives,
its output value, and the associated
teacher (supervisor) response.
The Perceptron Training Algorithm
The weight vector is changed according to the
following:
w(i 1) w(i ) w(i )
where
w(i ) cr w(i ), x(i ), d (i ) x(i )
and
• d(i) is the teacher’s (supervisor’s) signal
• r is the learning signal
•c is a positive number called the learning
constant depending on the sign of r.
The Perceptron Training Algorithm
Here we have used
∇
f ( w t x( i ))
w
1
x (i )
t
( w x( i )) 1
x2 (i )
t
(w x( i )) =
x( i )
w2
x
(
i
)
n1
( w t x( i ))
w
n 1
This reveals that the change in the weight
vector is in the direction of steepest ascent
(or descent)of wtx(i).
The Perceptron Training Algorithm
Perceptron Learning (Traning) Rule (Algorithm).
In this case the learning signal is defined as:
r (i ) d (i ) y (i )
where d(i) is the desired output signal and y(i) is
the actual output signal for the input pattern x(i)
given by:
y (i ) sgn( w (i) x(i) )
t
The weight adjustment is given by:
w(i ) c[d (i ) sgn( w (i ) x (i ))] x (i )
t
The Perceptron Training Algorithm
d = 1, i.e.,class 1 is input :
1) y =sgn( wt x) 1,i.e., the input is misclassified r d y 1 (1) 2;
the correction is in the direction of steepest ascent and given as w(i) 2c x(i)
2) y =sgn( wt x) 1,i.e., the input is correctly classified r d y 1 1 0; no correction
d = -1, i.e.,class 2 is input :
1) y sgn( wt x) 1,i.e., the input is correctly classified r d y 1 (1) 0; no correction
2) y sgn(wt x) 1,i.e., the input is misclassified r d y 1 (1) 2;
the correction is in the direction of steepest decent and given as w(i) 2c x(i)
The Perceptron Training Algorithm
EXAMPLE:
The
trained classifier should provide the
following classification of four patterns x
with known class membership d:
x(1)= 1, x(3) =3,
x(2)= -0.5, x(4)=-2,
d1= d3 = 1: class C1
d2 = d4 = -1: class C2
The Perceptron Training Algorithm
The augmented input vectors are given as:
1
0.5
3
2
x(1) , x(2)
, x(3) , x(4)
1
1
1
1
x(
x
x(1)
x
The Perceptron Training Algorithm
Let us choose an arbitrary augmented weight vector of
2.5
w(1)
1.75
With x (1) being the input , we obtain
1
wt (1) x(1) 2.5 1.75 0.75 0
1
and binary activation function (discrete
perceptron)
sgn( wt (1) x(1)) 1
Hence x(1) is classified as being in class C2. However
this is not true. Therefore a correction has to be made.
The Perceptron Training Algorithm
The question to be asked at this point is: How do we make
this correction? The answer depends on which training
algorithm used. Since sgn{wt(1)x(1)}=-1, one thing is
certain,however, is that the correction should me made in
such a way that
t
wx
increases. In order that we achieve this we must first find
out if there is a direction in which the decrease or, for that
matter, increase takes place. To show this, let us consider
the surface given by :
The Perceptron Training Algorithm
z f ( w1 , w2 ,....., wn1 )
We can write:
df ( w1 , w2 ,....., wn1 )
f ( w1 , w2 ,....., wn1 )
f ( w1 , w2 ,....., wn1 )
f ( w1 , w2 ,....., wn1 )
dw1
dw2 .....
dwn1
w1
w2
wn1
Let us now restrict ourselves to the case of
3 dimensions, namely,
z , w1 , w2
or more succinctly
z , x, y
The Perceptron Training
Algorithm
Now consider the surface
z f ( x, y )
If the level curves are interpreted as contour lines
of the landscape, i.e., of the surface, then along
these curves
z f ( x, y ) constant
The Perceptron Training
Algorithm
consequently, we obtain
dz df ( x, y ) 0
hence
f ( x , y )
f ( x , y )
dx
dy 0
df ( x , y )
x
y
where dx and dy are the increments given to
x and y on the level curve.
The Perceptron Training
Algorithm
Now defining
f ( x , y )
x
dx
f ( x , y ) f ( x , y ) and dr
dy
y
where
f
and dr
are known to be the gradient vector and the tangent
vector,respectively,
The Perceptron Training Algorithm
we can write
df ( x , y ) f dr 0
t
This means that the gradient vector and the
tangent vector are orthogonal vectors. Moreover
it can be shown that the gradient vector points in
the direction of steepest ascent of the function
f(x,y). Furthermore, the gradient is the rate of
climb in the direction of steepest ascent.
The Perceptron Training Algorithm
Now consider the surface
z f ( x, y ) ( x 50) ( y 50) 32
2
2
The following MATLAB program plots this
surface:
2
The Perceptron Training Algorithm
close all
clear all
for x=1:1:100;
for y=1:1:100;
f(x,y)=(x-50).^2+(y-50).^2-1024;
end
end
mesh(f);title('f(x,y)=x^2+y^2-1024');
figure,imshow(f,[ ],'notruesize');colormap(jet);
colorbar;title('f(x,y)=x^2+y^2-1024');
The Perceptron Training Algorithm
z=f(x,y)=(x-50)2+(y-50)2-322
z=f(x,y)=(x-50)2+(y-50)2-322
4000
3000
4000
3000
2000
2000
1000
1000
0
0
-1000
-1000
-2000
100
100
80
50
-2000
100
60
50
40
0
20
0
0
20
0
z=f(x,y)=(x-50)2+(y-50)2-322
3500
3000
2500
2000
1500
1000
500
0
-500
-1000
40
60
80
100
The Perceptron Training Algorithm
The level curves are obtained from
z f ( x, y ) ( x 50) ( y 50) 32 Ci
2
2
2
where Ci are constants.
y
C3 16384
C2 9216
C1 4096
x
The Perceptron Training Algorithm
f ( x, y )
x 2( x 50)
dx
f ( x, y )
and dr dy
(
,
)
f
x
y
2(
50)
y
y
Considering the four quadrants of the circle:
Q.1 2( x 50) 0
Q.2 2( x 50) 0
2( y 50) 0
Q.3 2( x 50) 0
2( y 50) 0
Q.4 2( x 50) 0
2( y 50) 0
2( y 50) 0
The Perceptron Training Algorithm
the gradient vector points in directions as given
below:
Q.2
Q.1
Q.3
Q.4
The Perceptron Training Algorithm
The fact that the gradient vector is orthogonal to
the tangent vector proves that it is in the direction
of steepest ascent or steepest descent.
The directions found for the example show that
the gradient vector points in the direction of ascent
of the function f(x,y).
Combining the two facts we can conclude that it
points in the direction of steepest ascent.
The Perceptron Training Algorithm
x1( 4 ) 2
x1( 3 ) 3
x ( 2 ) 0.5
x ( 1 ) 1
,
x
(
)
x( 1 ) 1 , x( 2 ) 1
,
x
(
)
3
4
x2 ( 4 ) 1
x2 ( 3 ) 1
x2 ( 2 ) 1
x2 ( 1 ) 1
In the weight space the following straight lines
represent the decision lines:
w1
w1
1
w2 w1 w2 0 w2 w1
1
0.5
w2
w1 0.5w2 0 w2 0.5w1
1
w1
3
w2 w1 3w2 0 w2 3w1
1
w1
2
w2 w1 2 w2 0 w2 2 w1
1
The Perceptron Training Algorithm
Decision lines in
weight space
w2
Initial weight vector
x(2)
x(4)
x(1)
x(3)
w1
2
4
3
1
The Perceptron Training
Algorithm
The corresponding gradient vectors
are computed as follows:
The Perceptron Training Algorithm
for x( 1 )
( wt x( 1 ))
x ( 1 )
1
w
1
t
t
1
x
(
)
w x( 1 ) w1 w2 ( w x( 1 ))
1
t
1
( w x( 1 )) x1( 1 )
w
2
for x( 2 )
( wt x( 2 ))
x ( 2 )
0.5
w
1
t
t
1
x
(
)
w x( 1 ) 0.5w1 w2 ( w x( 2 ))
2
t
1
( w x( 2 )) x1( 2 )
w
2
for x( 3 )
( wt x( 3 ))
x ( 3 )
3
w
1
t
t
1
w x( 3 ) 0.5w1 w2 ( w x( 3 ))
t
x( 3 ) 1
( w x( 3 )) x1( 3 )
w
2
for x( 4 )
( wt x( 4 ))
x ( 4 )
2
w
1
t
t
1
x
(
)
w x( 4 ) 2 w1 w2 ( w x( 4 ))
4
t
1
( w x( 4 )) x1( 4 )
w
2
The Perceptron Training Algorithm
wtx(3)<0
wtx(3)>0
w2
Decision lines and
gradient vectors in
weight space
Initial weight vector
2.5
w(1)
1.75
2
wtx(2)>0
wtx(2)<0
x(2)
x(4)
x(1)
x(3)
w1
wtx(4)>0
4
wtx(1)>0
wtx(4)<0
wtx(1)<0
3
1
The Perceptron Training Algorithm
Now we can concentrate on the particular training
(or learning) algorithm (or rule).
The Perceptron Training Algorithm
This is a supervised learning algorithm. This
means that at each step the correction is made
according to the directive given by the supervisor
as shown in the following figure.
The Perceptron Training Algorithm
yi
x
di
Weight learning rule: di is provided only in the
case of supervised learning
The Perceptron Training Algorithm
Now consider
r d i sgn( w x )
t
Since
d i 1 , sgn( w x ) 1
t
r can take on one of the three values:
2, 2, 0
The Perceptron Training Algorithm
forIn fact
d i 1, sgn( w x ) 1 r 2
t
for
d i 1, sgn( w x ) 1 r 2
t
for Since
d i 1, sgn( w x ) 1 r 0
t
and
d i 1, sgn( w x ) 1 r 0
t
Therefore we can define the correction rule in terms
of the correction amount at the nth step as follows:
Δwi ( n ) ( n )( d i ( n ) sgn( w ( n )x( n )))( w ( n )x( n ))
t
t
The Perceptron Training Algorithm
Δwi ( n ) ( n )( d i ( n ) sgn( w ( n )x( n )))x( n )
t
yi
di
The Perceptron Training
Algorithm
In order for the correct cllasification of the entire
x( 1 ), x( 2 ), x( 3 ), and x( 4 )
training set
with respective class memberships
d ( 1 ) 1, d ( 2 ) 1, d ( 3 ) 1; and d ( 4 ) 1
the following four inequalities must hold:
t
w ( N )x( 1 ) 0
w ( N )x( 2 ) 0
t
wt ( N )x( 3 ) 0
wt ( N )x( 4 ) 0
where w(N) is the final weight vector that provides
correct classification for the entire training set.
The Perceptron Training
Algorithm
This means that after N-1 training steps
the weight vector w(N) ends up in the
solution area, which is the shaded area
in the following figure.
The Perceptron Training Algorithm
Weight Space
wtx(3)<0 wtx(3)>0
w2
Initial weight vector
2.5
w(1)
1.75
2
x(2)
x(4)
x(1)
wtx(2)>0
wtx(2)<0
x(3)
w1
wtx(1)>0
wtx(4)>0 wtx(4)<0
4
wtx(1)<0
3
1
The Perceptron Training
Algorithm
The training has so far been shown in the weight
space. This is achieved using the decision lines
defined by x(1), x(2), x(3) nd x(4). However, the
original decision lines determined by the
perceptron at each step are defined in the pattern
space as this enables the classification to be easily
seen. These decision lines are defined by w(1), w(2)
w(3) and w(4).
In the following we show the correction steps of the
weight vector as well as the corresponding decision
surfaces in the pattern space.
The Perceptron Training
Algorithm
In the pattern space
w( 1 )x 0
determines the the decision line defined by
the initial weight vector
2.5
w(1)
1.75
as
x1
w (1) x 2.5 1.75 2.5 x1 1.75 x2 0 x2 1.429 x1
x2
t
The Perceptron Training
Algorithm
The corresponding gradient vector is computed
as follows:
( wt ( 1 )x )
w ( 1 )
2.5
x
1
t
t
1
w ( 1 )x 2.5 x1 x2 ( w ( 1 )x
w
(
1
)
t
1.75
( w ( 1 )x ) w2 ( 1 )
x2
which is the initial weight vector. As the
gradient vector lies on the side of
w (1) x 2.5 x1 1.75 x2 0
t
where
w (1) x 2.5 x1 1.75 x2 0
t
The Perceptron Training
Algorithm
However,
x(1) and x(3) have class 1 ,i.e.,
d1= d3=1 and x(2) and x(4) have class 2 ,i.e.,
d2= d4=-1.
This means that x(1), x(2), x(3), x(4) all are
wrongly classified.
The Perceptron Training
Algorithm
Weight Space
Initial
weight
vector
2.5
w( 1 )
1.75
Pattern Space
x
wt ( 1 )x 2.5 1.75 1 2.5 x1 1.75 x2 0 x2 1.429 x1
x2
Initial
decision
line
Weight vector is orthogonal to corresponding decision line
The Perceptron Training Algorithm
Weight Space
w2
Pattern Space
x2
wt ( 1 ) x 0
w( 1 ) (is orthogonal todecion line)
x(2)
Initial weight vector
w1
x(4)
wt ( 1 ) x 0
x(1)
2.5
w(1)
1.75
x
wt ( 1 )x 2.5 1.75 1 2.5 x1 1.75 x2 0 x2 1.429 x1
x2
Decision line for initial weight vector
x(3)
x1
The Perceptron Training
Algorithm
Pattern x(1) is input
Weight Space
Pattern Space
Initial
weight
vector
2.5
w( 1 )
1.75
x
wt ( 1 )x 2.5 1.75 1 2.5 x1 1.75 x2 0 x2 1.429 x1
x2
Initial
decision
line
Weight vector is orthogonal to corresponding decision line
Initial
decision
line
wt x( 1 ) w1
1
w2 w1 w2 0 w2 w1
1
1
x( 1)
1
First
input
vector
Decision line is orthogonal to corresponding input vector
The Perceptron Training Algorithm
Step 1:Pattern x(1) is input
Weight Space
Pattern Space
w2
1
x2
wt ( 1 ) x 0
w( 1 )
wt x( 1 ) 0
x(1)
Initial weight vector
2.5
w(1)
1.75
wt x( 1 ) w1
x(2)
w1
wtx(1)>0
wtx(1)<0
1
w2 w1 w2 0 w2 w1
1
x(4)
wt ( 1 ) x 0
x(1)
x(3)
x1
Line 1 is
decision line
x
wt ( 1 )x 2.5 1.75 1 2.5 x1 1.75 x2 0 x2 1.429 x1
x2
The Perceptron Training
Algorithm
Step 1 (Update 1): Pattern x(1) is input
Weight Space
Pattern Space
Initial weight First input
Initial decision line
vector
vector
2.5
w( 1 )
1.75
1
x( 1)
1
x
wt ( 1 )x 2.5 1.75 1 2.5 x1 1.75 x2 0 x2 1.429 x1
x2
1
y( 1 ) sgn( wt ( 1 )x( 1 )) sgn( 2.5 1.75 ) 1
1
d ( 1 ) y( 1 ) 1 ( 1 ) 2
Updated weight vector
2.5 1 1.5
w(2) w(1) x(1)
1.75 1 2.75
Updated decision line
x
wt ( 2 )x 1.5 2.75 1 1.5 x1 2.75 x2 0 x2 0.545 x1
x2
The Perceptron Training Algorithm
Step 1 (Update 1): :Pattern x(1) is input
Weight Space
Pattern Space
1.5
w( 2 )
w2
x2
2.75
w( 2 )
wt ( 2 ) x 0
wt x( 1 ) 0
x(1)
Initial weight vector
2.5
w(1)
1.75
wt x( 1 ) w1
x(2)
x(4)
w1
wt ( 2 ) x 0
wtx(1)>0
wtx(1)<0
1
w2 w1 w2 0 w2 w1
1
x(1)
2
x(3)
x1
Line 2 is
decision line
x
wt ( 2 )x 1.5 2.75 1 1.5 x1 2.75 x2 0 x2 0.545 x1
x2
The Perceptron Training
Algorithm Pattern Space
Weight Space
Step 2 (Update 2): :Pattern x(2) is input
Weight
vector to be
updated
1.5
w( 2 )
2
.
75
Second
input
vector
0.5
x( 2 )
1
Decision line to be updated
x
wt ( 2 )x 1.5 2.75 1 1.5 x1 2.75 x2 0 x2 0.545 x1
x2
0. 5
y( 2 ) sgn( wt ( 2 )x( 2 )) sgn( 1.5 2.75
) 1
1
d ( 2 ) y( 2 ) 1 1 ) 2
Second update
1.5 0.5 1
w(3) w(2) x(2)
1 1.75
2.75
Updated decision line
x
wt ( 3 )x 1 1.75 1 x1 1.75 x2 0 x2 0.57 x1
x2
The Perceptron Training Algorithm
Step 2 (Update 2): :Pattern x(2) is input
Weight Space
Pattern Space
w( 3 ) w2
x2
w( 3 )
wt ( 3 ) x 0
wt x( 2 ) 0
wtx(2)>0
x(2)
Initial weight vector
wtx(2)<0
w1
w1
x(2)
x(4)
0 .5
w2
w1 0.5w2 0 w2 0.5w1
1
3
x(1)
x(3)
w t ( 3 ) x 0 x1
Line 3 is
decision line
The Perceptron Training
Algorithm Pattern Space
Weight Space
Step 3 (Update 3): :Pattern x(3) is input
Weight
vector to be
updated
1
w( 3 )
1.75
Third
input
vector
Decision line to be updated
3
x( 3 )
1
x
wt ( 3 )x 1 1.75 1 x1 1.75 x2 0 x2 0.57 x1
x2
Step 3:Pattern x(3) is input
3
y( 3 ) sgn( w ( 3 )x( 3 )) sgn( 1 1.75 ) 1
1
t
d ( 3 ) y( 3 ) 1 ( 1 ) 2
1 3 2
w(4) w(3) x(3)
1.75 1 2.75
Updated decision line
x
wt ( 4 )x 2 2.75 1 2 x1 2.75 x2 0 x2 0.73 x1
x2
The Perceptron Training Algorithm
Step 3 (Update 3): Pattern x(3) is input
Weight Space
Pattern Space
w2
x2
w(4)
wt x( 3 ) 0
wtx(3)>0
Initial weight vector
x(3)
x(4)
w1
wtx(3)<0
w1
wt ( 4 ) x 0
3
w2 3w1 w2 0 w2 3w1
1
x(2)
wt ( 4 ) x 0
x(1)
x(3)
x1
4
Line 4 is
decision line
The Perceptron Training
Algorithm Pattern Space
Weight Space
Step 4 (Update 4): :Pattern x(4) is input
Weight
vector to be
updated
2
w( 4 )
2.75
Fourth
input
vector
Decision line to be updated
2
x( 4 )
1
x
wt ( 4 )x 2 2.75 1 2 x1 2.75 x2 0 x2 0.73 x1
x2
Step 4:Pattern x(4) is input
2
y( 4 ) sgn( w ( 4 ) x( 4 )) sgn( 2 2.75 ) 1
1
t
d ( 4 ) y( 4 ) 1 ( 1 ) 0
2
w(5) w(4)
2.75
No update,
same decision line
x
wt ( 4 )x 2 2.75 1 2 x1 2.75 x2 0 x2 0.73 x1
x2
The Perceptron Training Algorithm
Step 4 (Update 4): Pattern x(4) is input
Weight Space
Pattern Space
w2
x2
w(5) =w(4)
wt x( 4 ) 0
x(2)
x(4)
Initial weight vector
wtx(4)>0
w1
wt ( 4 ) x 0
w1
wtx(4)<0
2
w2 2 w1 w2 0 w2 2 w1
1
x(4)
wt ( 4 ) x 0
x(1)
x(3)
x1
5 =4
Line 4 remains
decision line
The Perceptron Training
Algorithm
Step 5 (Update5): :Pattern x(1) is input
Weight
vector to be
updated
First
input
vector
2
w( 5 ) w( 4 )
2.75
1
x( 1)
1
Decision line to be updated
x
wt ( 4 )x 2 2.75 1 2 x1 2.75 x2 0 x2 0.73 x1
x2
Step 5:Pattern x(1) is input
1
y( 5 ) sgn( wt ( 5 ) x( 1 )) sgn( wt ( 4 )x( 1 )) sgn( 2 2.75 ) 1
1
d ( 1 ) y( 5 ) 1 1 0
2
w(6) w(5) w(4)
2.75
No update,
same decision line
x
wt ( 4 )x 2 2.75 1 2 x1 2.75 x2 0 x2 0.73 x1
x2
The Perceptron Training Algorithm
Step 5 (Update5): :Pattern x(1) is input
Weight Space
Pattern Space
w2
x2
w(6) =w(5)= w(4)
wt x( 1 ) 0
x(1)
w1
Initial weight vector
wtx(1)<0
w1
wtx(1)>0
1
w2 w1 w2 0 w2 w1
1
wt ( 4 ) x 0
x(2)
x(4)
wt ( 4 ) x 0
x(1)
x(3)
x1
6 5 4
Line 4 remains
decision line
The Perceptron Training
Algorithm
Step 6 (Update 6): :Pattern x(2) is input
Weight
vector to be
updated
Second
input
vector
Decision line to be updated
0.5
2
w( 6 ) w( 5 ) w( 4 )
x( 2 )
2
.
75
1
x
wt ( 4 )x 2 2.75 1 2 x1 2.75 x2 0 x2 0.73 x1
x2
Step 6:Pattern x(2) is input
0.5
y (6) sgn( wt (6) x(2)) sgn( wt (6) x(2)) sgn( 2 2.75
) 1
1
d ( 2 ) y( 6 ) 1 1 ) 2
Updated decision line
2 0.5 2.5 t
x1
w( 7 ) w( 4 ) x( 2 )
w
(
7
)
x
2
.
5
1
.
75
x 2.5x1 1.75x2 0x2 1.43x1
2
2.75 1 1.75
The Perceptron Training Algorithm
Step 6 (Update 6): :Pattern x(2) is input
Weight Space
Pattern Space
w2
x2
w(7)
wt x( 2 ) 0
wt ( 7 ) x 0
wtx(3)>0
Initial weight vector
w(7)
x(3)
x(4)
w1
x(2)
x(1)
7
wtx(3)<0
w1
2
w2 2 w1 w2 0 w2 2 w1
1
x(3)
x1
wt ( 7 ) x 0
The Perceptron Training Algorithm
Step 7 (Update 7): :Pattern x(3) is input
Weight Space
Pattern Space
w2
x2
w(4)
wt x( 3 ) 0
wtx(3)>0
x(2)
Initial weight vector
x(2)
w1
x(4)
wtx(3)<0
w1
wt ( 3 ) x 0
3
w2 3w1 w2 0 w2 3w1
1
3
x(1)
x(3)
w t ( 3 ) x 0 x1
The Perceptron Training
Algorithm
Step 7:Pattern x3 is input
3
y (7) sgn( wt (7) x(3)) sgn( 2.5 1.75 ) 1
1
d ( 3 ) y( 7 ) 1 1 0
2.5
w(8) w(7)
1.75
The Perceptron Training
Algorithm
Step 8:Pattern x4 is input
2
y( 8 ) sgn( w ( 8 )x( 4 )) sgn( w ( 7 )x( 4 )) sgn( 2.5 1.75 ) 1
1
t
t
d ( 4 ) y( 7 ) 1 ( 1 ) 0
2.5
w(9) w(8) w(7)
1.75
The Perceptron Training
Algorithm
Step 9:Pattern x(1) is input
1
y( 9 ) sgn( w ( 9 )x( 1 )) sgn( w ( 7 )x( 1 )) sgn( 2.5 1.75 ) 1
1
t
t
d ( 1 ) y( 9 ) 1 1 0
2.5
w(10) w(9) w(8) w(7)
1.75
The Perceptron Training
Algorithm
Step 10:Pattern x(2) is input
1
y( 10 ) sgn( w ( 10 )x( 2 )) sgn( w ( 7 )x( 1 )) sgn( 2.5 1.75 ) 1
1
t
t
d ( 2 ) y( 10 ) 1 1 2
2.5
w(11)
1.75
The Perceptron Training
Algorithm
The Perceptron Training Algorithm
Pattern Space
x2
Weight Space
w2
wt x( 1 ) 0
wt ( 1 ) x 0
w( 1 )
x(1)
Initial weight vector
2.5
w(1)
1.75
wt x( 1 ) w1
x(2)
w1
x(4)
wt ( 1 ) x 0
x(1)
wtx(1)>0
wtx(1)<0
1
w2 w1 w2 0 w2 w1
1
x
wt ( 1 )x 2.5 1.75 1 2.5 x1 1.75 x2 0 x2 1.429 x1
x2
x(3)
x1
The Perceptron Training Algorithm
The initial weight vector w(1) and the weight
vectors w(2)- w(11) obtained during the training
algorithm are given below:
2.5
1.5
1
2
, w(2)
, w(3)
, w(4)
,
w(1)
1.75
2.75
1.75
2.75
2.5
w(5) w(4), w(6) w(5) w(4), w(7)
,
1.75
3
w(8) w(7), w(9) w(8) w(7), w(10) w(9) w(8) w(7), w(11)
0.75
As can be seen from these vectors, out of the ten
vectors w(2)- w(11) only five are different .
The Perceptron Training Algorithm
These five vectors are given in the MATLAB plot
below:
3
2.5
2
1.5
1
0.5
0
-0.5
-1
-1.5
-2
-8
-6
-4
-2
0
2
4
6
8
10
12
The Perceptron Training Algorithm
x3
Example: The trained
(0,0,1)
classifier is required
to provide the
(0,0,1)
classification such
that the yellow vertices (0,1,1)
0
of the cube have class
(0,0,0)
membership d=1 and
the blue vertices have
(0,1,0)
class membership
d=2.
x2
(1,0,1)
x1
(1,0,0)
(1,1,0)
x3=0.25 plane
The Perceptron Training Algorithm
The Perceptron Training Algorithm
SUMMARY OF CONTINUOUS PERCEPTRON TRAINING ALGORITHM
Given are the p training pairs
{x1,d1, x2,d2,…………….,xp,dp}, where xi is (N+1) x 1
Di is 1 x 1, i=1,2, ,P. In the following n denotes
the training step and p denotes the step counter
within the training cycle.
Step 1: c>0 is chosen.
Step2: Weights are initialized at w at random small
values, w is (N+1) x 1. Counters and error are
initialized.
1 k ,1 p and 0 E
The Perceptron Training Algorithm
Step3: The training cycle begins here. Input is
presented and output is computed:
x p x, d p d , y sgn( w x)
t
Step4: Weights are updated:
→
x p x, w
1
w c(d y ) x
2
Step5: Cycle error is computed.
1
E (d y )2
2
The Perceptron Training Algorithm
Step 6: If p<P then
p p 1, n n 1
and go to Step 3, otherwise go to Step 7.
Step 7: The training cycle is completed. For E=0,
terminate the training session. Output weights, k
and E. If E>0 then enter the new training cycle
by going to Step 3.
Single-Layer Continuous
Perceptron
1
2
Here the activation function is a continuous function of
the weights instead of the signum.
There are two main objectives of this:
To define a continuous function of the weights as the
error function so as to obtain finer control over the
weights as well as over the whole training procedure;
To enable the computation of the error gradient in
order to be continuously in a position to know the
direction in which the error decreases.
Training Rule for a Single-Layer
Continuous Perceptron:The Delta
Training Rule
The Delta Training Rule is based on the
minimisation of the error function which is given by
1
2
E( n ) ( d ( n ) y( n ))
2
where n is a positive integer representing the traning
step number, i.e.,the step number in the minimisation
process, d(n) is the desired output signal and
t
y (n) f [ w (n) x(n)]
is the actual output.
Training Rule for a Single-Layer
Continuous Perceptron:The Delta
Training Rule
The error function (error surgface) is a function
of the weights: E(w1,w2,....,wp)=E(w) which is
minimised using an iterative minimisation
method which computes the new values of the
weights according to
w(n 1) w(n) w(n)
where w(n) is the increment given to the
present weight vector w(n) to obtain the new
weight vector w(n+1).
Training Rule for a Single-Layer
Continuous Perceptron:The Delta
Training Rule
Let us now use the steepest descent method for the
minimisation of the error function E(w) where it is
required that the weight changes be in the negative
gradient direction. Therefore we take:
∇
w(n) E ( w(n))
where E(w(n)) is the gradient vector and is called the
learning constant. Using this in the equation above, we obtain
w( n 1 ) w( n ) E( w( n ))
Training Rule for a Single-Layer
Continuous Perceptron:The Delta
Training Rule
E( w( n )) E( n )
is the error surface at the n’th training step .
Therefore the error to be minimised is:
1
E( n ) ( d ( n ) f ( wt ( n )x( n ))2
2
The independent variables for minimisation at
each training step are wi, the components of the
weight vector.
Training Rule for a Single-Layer
Continuous Perceptron:The Delta
Training Rule
The error minimisation requires the computation
of the gradient of the error function:
E( w )w w( n )
1
2
t
( d ( n ) f ( w x( n ))
2
w w( n )
Training Rule for a Single-Layer
Continuous Perceptron:The Delta
Training Rule
The gradient vector is defined as:
E
w
1
E
w2
E ( w )
.
.
E
w
p 1
Training Rule for a Single-Layer
Continuous Perceptron:The Delta
Training Rule
Using
E( w )w w( n )
1
t
2
( d ( n ) f ( w x( n ))
2
w w( n )
and defining
v( w ) w x
t
we obtain
Training Rule for a Single-Layer
Continuous Perceptron:The Delta
Training Rule
E( w )ww( n )
v( w )
w
1
v( w )
df ( v( w )) w2
d ( n ) f ( v( w ))
.
dv
.
v( w )
w
p 1 w w( n )
Training Rule for a Single-Layer
Continuous Perceptron:The Delta
Training Rule
Since
and
we can write
v( w)
xi
wi
f(v) y
Training Rule for a Single-Layer
Continuous Perceptron:The Delta
Training Rule
E ( w)w w( n )
df (v( w))
d ( n) y ( n)
x ( n)
dv ww ( n )
and
E ( w)
df (v( w))
x i ( n)
d ( n) y ( n)
dv ww ( n )
wi ww( n )
Training Rule for a Single-Layer
Continuous Perceptron:The Delta
Training Rule
If bipolar continuous activation function is used
then we have:
v
and
1 e
f (v )
v
1 e
v
df (v)
2e
v 2
dv
(1 e )
Training Rule for a Single-Layer
Continuous Perceptron:The Delta
Training Rule
In fact
v
df (v)
2e
v 2
dv
1 e
v 2
1 e
1
1
2
1
(v)
1
f
v
2 1 e 2
Training Rule for a Single-Layer
Continuous Perceptron:The Delta
Training Rule
E( w )w w( n )
1
d ( n ) y( n )1 y 2 ( n ) x( n )
2
Training Rule for a Single-Layer
Continuous Perceptron:The Delta
Training Rule
Conclusion: The delta training rule for the
bipolar continuous perceptron is given as:
1
2
w( n 1 ) w( n ) d ( n ) y( n )1 y ( n ) x( n )
2
Training Rule for a Single-Layer
Continuous Perceptron:The Delta
Training Rule
If unipolar continuous activation function is used
then we have:
and
1
f (v )
v
1 e
v
df (v)
e
v 2
dv
(1 e )
Training Rule for a Single-Layer
Continuous Perceptron:The Delta
Training Rule
we can write
df (v)
e v
1 1 ev 1
1
1
(1
)
2
v
v
v
v
v
1 e
1 e
dv
1 e 1 e 1 e
=f (v)(1 f (v))
Training Rule for a Single-Layer
Continuous Perceptron:The Delta
Training Rule
Example:We will carry out the same
training algorithm as in the previous
example but this time using a continuous
bipolar perceptron.
The error at step n is given by:
2
1
1 e
1
2
d ( n )
1
E ( n ) d ( n )
v( n )
v( n )
2
1 e
2
1 e
v( n )
2
Training Rule for a Single-Layer
Continuous Perceptron:The Delta
Training Rule
For the first pattern x(1)=[1 1]t , d(1)=1.
The error at step 1 is given by:
2
1
2
E (1) d (1)
1
( w1 w2 )
2
1 e
2
2
1
2
2
1 2e
1
1
( w1 w2 )
( w1 w2 )
( w1 w2 ) 2
e
e
2 1 e
2
1
(1
)
( w1 w2 )
Training Rule for a Single-Layer
Continuous Perceptron:The Delta
Training Rule
For the second pattern x(2)=[-0.5 1]t ,
d(2)=-1.
The error at step 2 is given by:
2
1
2
1
E ( 2 ) d ( 2 )
( 0.5 w1 w2 )
2
1 e
2
1
2
1
2
2
1
1
( 0.5 w1 w2 )
( 0.5 w1 w2 )
2 1 e
2
1 e
1 e( 0.5 w1 w2 )
2
2
Training Rule for a Single-Layer
Continuous Perceptron:The Delta
Training Rule
For the third pattern x(3)=[3 1]t , d(3)=1.
The error at step 3 is given by:
2
1
2
1
E ( 3 ) d ( 3 )
( 3 w1 w2 )
2
1 e
2
2
1
2
1 2e
2
1
1
( 3 w1 w2 )
( 3 w1 w2 )
( 3 w1 w2 )
2
2 1 e
1 e
1
e
( 3 w1 w2 )
2
Training Rule for a Single-Layer
Continuous Perceptron:The Delta
Training Rule
For the fourth pattern x(4)=[-2 1]t , d(4)=-1.
The error at step 4 is given by:
2
1
2
1
E ( 4 ) d ( 4 )
( 2 w1 w2 )
2
1 e
2
1
2
1
2
2
1
1
( 2 w1 w2 )
( 2 w1 w2 )
2
2 1 e
1 e
1 e( 2 w1 w2 )
2
2
Training Rule for a Single-Layer
Continuous Perceptron:The Delta
Training Rule
close all;
clear all;
[w1,w2] = meshgrid(-4:.1:4, -4:.1:4);
Z1 = exp(w1+w2);
E1=2./(1+Z1).^2
mesh(Z1)
Z2 = exp(.5*w1-w2);
E2=2./(1+Z2).^2
figure,mesh(Z2)
Z3 = exp(3*w1+w2);
E3=2./(1+Z3).^2
figure,mesh(Z3)
Z4 = exp(2*w1-w2);
E4=2./(1+Z4).^2
figure,mesh(Z4)
subplot(2,2,1),mesh(E1);title('Error surface for xt(1)=[1 1] and y=f(wt*x(1))');
xlabel('w1'),ylabel('w2'),zlabel('E1(w1,w2)');
Training Rule for a Single-Layer
Continuous Perceptron:The Delta
Training Rule
subplot(2,2,2),mesh(E2);title('Error surface for xt(2)=[.5 -1] and y=f(wt*x(2))');
xlabel('w1'),ylabel('w2'),zlabel('E2(w1,w2)');
subplot(2,2,3),mesh(E3);title('Error surface for xt(3)=[3 1] and y=f(wt*x(3))');
xlabel('w1'),ylabel('w2'),zlabel('E3(w1,w2)');
subplot(2,2,4),mesh(E4);title('Error surface for xt(4)=[2 -1] and y=f(wt*x(4))');
xlabel('w1'),ylabel('w2'),zlabel('E4(w1,w2)');
E = E1+E2+E3+E4;
figure,mesh(E);title('Total Error
E(w1,w2)=E1(w1,w2)+E2(w1,w2)+E3(w1,w2)+E4(w1,w2),MESH');
xlabel('w1'),ylabel('w2'),zlabel('E(w1,w2)');
figure,imshow(E,[],'notruesize');colormap(jet);title('Total Error
E(w1,w2)=E1(w1,w2)+E2(w1,w2)+E3(w1,w2)+E4(w1,w2),IMSHOW');
xlabel('w1'),ylabel('w2')
The error surfaces for the above four cases are
shown in the next slide:
Training Rule for a Single-Layer Continuous
Perceptron:The Delta Training Rule
Error surface for xt(1)=[1 1] and y=f(wt*x(1))Error surface for xt(2)=[.5 -1] and y=f(wt*x(2))
2
E2(w1,w2)
E1(w1,w2)
2
1
0
0
100
50
w1
100 0
1
0
100
100
50
50
w2
w2
0 0
50
w1
Error surface for xt(3)=[3 1] and y=f(wt*x(3))Error surface for xt(4)=[2 -1] and y=f(wt*x(4))
2
E4(w1,w2)
E3(w1,w2)
2
1
1
0
100 100
0
0
50
w1
100 0
50
w2
50
w2
0 0
50
w1
100
Training Rule for a Single-Layer
Continuous Perceptron:The Delta
Training Rule
The total error is defined by:
E( w1 , w2 ) E1( w1 , w2 ) E2 ( w1 , w2 ) E3 ( w1 , w2 ) E4 ( w1 , w2 )
The total error surface is shown in the next
slide.
Training Rule for a Single-Layer Continuous
Perceptron:The Delta Training Rule
Training Rule for a Single-Layer Continuous
Perceptron:The Delta Training Rule
A contour map of the total error is depicted below:
Training Rule for a Single-Layer Continuous
Perceptron:The Delta Training Rule
The classifier training has been simulated for
= 0.5 for four arbitrarily chosen initial weight
vectors, including the one taken from
x(1)= 1, x(3) =3,
x(2)= -0.5, x(4)=-2,
d1= d3 = 1: class C1
d2 = d4 = -1: class C2
Training Rule for a Single-Layer Continuous
Perceptron:The Delta Training Rule
The resulting trajectories of 150 simulated
training steps are shown in the following figure
(each tenth step is shown).
Training Rule for a Single-Layer Continuous
Perceptron:The Delta Training Rule
In each case the weights converge during training
toward the center of the solution region obtained
for the discrete perceptron case given on the next
slide, which coincides with the dark blue region in
the contour map of the total error is depicted before
and also shown on the next slide.
Training Rule for a Single-Layer Continuous
Perceptron:The Delta Training Rule
Training Rule for a Single-Layer Continuous
Perceptron:The Delta Training Rule
SUMMARY OF CONTINUOUS PERCEPTRON TRAINING ALGORITHM
Given are the p training pairs
{x1,d1, x2,d2,…………….,xp,dp}, where xi is (N+1) x 1
Di is 1 x 1, i=1,2, ,P. In the following n denotes
the training step and p denotes the step counter
within the training cycle.
Step 1: >0, =1 and Emax>0 chosen.
Step2: Weights are initialized at w at random small
values, w is (N+1) x 1. Counters and error are
initialized.
1 k ,1 p and 0 E
Training Rule for a Single-Layer Continuous
Perceptron:The Delta Training Rule
Step3: The training cycle begins here. Input is
presented and output is computed:
x p x, d p d , y f ( w x )
t
Step4: Weights are updated:
1
x p x, w w (d y )(1 y 2 ) x
2
Step5: Cycle error is computed.
1
E (d y )2
2
Training Rule for a Single-Layer Continuous
Perceptron:The Delta Training Rule
Step 6: If p<P then
p p 1, n n 1
and go to Step 3, otherwise go to Step 7.
Step 7: The training cycle is completed. For E<Emax
terminate the training session. Output weights, k
and E. If E>Emax then enter the new training cycle
by going to Step 3.
Delta Training Rule for
Multi-Perceptron Layer
w11
w12
w21
x1
x2
wjk vk
xj
w1J
xJ
-1
v2
wK1
w1j
j-th
column
of nodes
v1
wK2
wKJ
vK
1
y1
2
y2
k
yk
K
yK
Neurons
k-th column of nodes
Delta Training Rule for
Multi-Perceptron Layer
The above can be redrawn as:
Delta Training Rule for
Multi-Perceptron Layer
v1 w11 x1 w12 x2 ......... w1 j x j ...... w1J xJ
y1 f ( v1 )
v2 w21 x1 w22 x2 ......... w2 j x j ...... w2 J xJ
y2 f ( v2 )
vl wl1 x1 wl 2 x2 ......... wlj x j ...... wlJ xJ
yl f (vl )
vK wK 1 x1 wK 2 x2 ......... wKj x j ...... wKJ xJ
y K f ( vK )
Delta Training Rule for
Multi-Perceptron Layer
v1 w11
v w
2 21
. .
. .
vK wK 1
w12
w22
.
.
wK 2
. . w1J x1
. . w1J x2
. .
. .
. .
. .
. . wKJ xJ
v Wx
v1
y1 f ( v1 )
y f ( v )
v2
2
2
. . Γ .
.
. .
yK f ( vJ )
v J
y Γ(v)
Delta Training Rule for
Multi-Perceptron Layer
y1 f (.)
y 0
2
. .
. .
yK 0
0 . .
f (.) . .
.
. .
.
0
. .
. .
v1
v
2
.
. .
f (.) vJ
0
0
.
y Γ[Wx]
Delta Training Rule for
Multi-Perceptron Layer
The desired and actual output vectors at the nth
training step are given as:
d1 (n)
d ( n)
2
d .
.
d K (n)
y1 (n)
y ( n)
2
y .
.
yK (n)
The error expression for a single perceptron was given as:
1
2
E( n ) ( d ( n ) y( n ))
2
Delta Training Rule for
Multi-Perceptron Layer
which can be generalised to include all squared errors at
the outputs k=1,2,.....,K
2
1 K
1
2
E( n ) ( d k ( n ) yk ( n )) d( n ) y( n )
2 k 1
2
where n represents the n-th step which corresponds
to a specific input pattern that produces the output error.
Delta Training Rule for
Multi-Perceptron Layer
The updated weight value from input j to
neuron k at step n is given by:
wkj ( n 1 ) wkj ( n ) Δwkj ( n )
According to the delta training rule for
continuous perceptron
E
Δwkj ( n )
wkj
w
k 1,2 ,..., K
for
j 1,2 ,..., J
kj wkj ( n )
where
Delta Training Rule for
Multi-Perceptron Layer
E
E vk
E E (v( w)) w v w
k
kj
kj
Using
vk wk1 x1 wk 2 x2 ......... wkj x j ...... wkJ xJ
we have
vk
xj
wkj
Delta Training Rule for
Multi-Perceptron Layer
The error signal term produced by the kth
neuron is defined as:
yk
Using this yields
E
vk
E
yk x j
wkj
Delta Training Rule for
Multi-Perceptron Layer
On the other hand we can write:
yk
E
E yk
vk
yk vk
Since
2
1 K
1
2
E( n ) ( d k ( n ) yk ( n )) d( n ) y( n )
2 k 1
2
we get
E
( d k yk )
yk
Delta Training Rule for
Multi-Perceptron Layer
On the other hand using
yk f ( vk )
vk
vk
yields
yk
E
E yk
f ( vk )
( d k yk )
vk
yk vk
vk
Delta Training Rule for
Multi-Perceptron Layer
which is used to obtain
f ( vk )
Δwkj ( n ) ( d k yk )
xj
vk
For bipolar continuous activation function
we already know that
f ( vk ) 1
1
2
2
1 ( f ( vk )) 1 yk
vk
2
2
Delta Training Rule for
Multi-Perceptron Layer
Hence
1
2
Δwkj ( n ) ( d k ( n ) yk ( n ))( 1 ( yk ( n )) )x j
2
and
1
wkj ( n 1 ) wkj ( n ) ( d k ( n ) yk ( n ))( 1 ( yk ( n ))2 )x j ( n )
2
where
Delta Training Rule for
Multi-Perceptron Layer
yk ( n ) ( d k ( n ) yk ( n ))( 1 ( yk ( n )) )
2
we can write
y1 ( n )
w11( n 1 ) . w1J ( n 1 ) w11( n ) . w1J ( n )
.
. x ( n ) . x ( n )
.
.
.
.
.
J
1
yK ( n )
wK 1( n 1 ) . wKJ ( n 1 ) wK 1( n ) . wKJ ( n )
Delta Training Rule for
Multi-Perceptron Layer
Now defining
x1 (n)
x ( n) .
xJ (n)
1 (n)
( n) .
J (n)
W (n 1) W (n) δy x
t
Generalised Delta Training Rule for
Multi- Layer Perceptron
z1
z2
.
t11
u1
t21
u2
.
zI
x2
uj
. t
j1
zi
.
.
x1
w11
v1
wk1
v2
wK1
wK2
wkj vk
xj
tIJ
i-th column of nodes
uJ
xJ
wkJ
j-th column of nodes (hidden layer)
vK
1
y1
2
y2
k
K
yk
yK
k-th column of nodes
Generalised Delta Training Rule for
Multi- Layer Perceptron
The weight adjustment for the hidden layer
according to the gradient descent method will be:
E
Δt ji ( n )
t ji
where
t ji t ji ( n )
j 1,2 ,..., J
for
i 1,2 ,..., I
E E u j
t ji u j t ji
Generalised Delta Training Rule for
Multi- Layer Perceptron
Here
E
xj
for
u j
j 1,2 ,...., J
is the error signal term of the hidden layer
with output x. This term is produced by the j-th
neuron of the hidden layer, where j=1,2,....,J.
On the other hand, using
u j t j1 z1 t j 2 z2 ............... t jI z I
Generalised Delta Training Rule for
Multi- Layer Perceptron
u
j
we can calculate
t ji
as
u j
Therefore
t ji
zi
E E u j
xj zi
t ji u j t ji
Generalised Delta Training Rule for
Multi- Layer Perceptron
and
Since
Δt ji xj zi
xj f ( uj )
E
E x j
xj
u j
x j u j
Generalised Delta Training Rule for
Multi- Layer Perceptron
E
1
2
d k f ( vk )
x j x j 2 k 1
K
and
x j
u j
f ( u j )
u j
Generalised Delta Training Rule for
Multi- Layer Perceptron
E
f ( vk )
( d k f ( vk )
x j
x j
k 1
K
f ( vk ) vk
( d k yk )
vk x j
k 1
K
Now using
vk wk1 x1 wk 2 x2 ......... wkj x j ...... wkJ xJ
Generalised Delta Training Rule for
Multi- Layer Perceptron
we have
vk
wkj
x j
Now using this equality and
yk
E
f ( vk )
( d k yk )
vk
vk
Generalised Delta Training Rule for
Multi- Layer Perceptron
in
E
f ( vk )
( d k f ( vk )
x j
x j
k 1
K
f ( vk ) vk
( d k yk )
vk x j
k 1
K
we obtain
Generalised Delta Training Rule for
Multi- Layer Perceptron
E
yk wkj
x j
k 1
K
vk
wkj in
Now using this and
x j
E
E x j
xj
u j
x j u j
Generalised Delta Training Rule for
Multi- Layer Perceptron
we obtain
xj
Now using
f ( u j )
u j
K
k 1
yk
wkj
Δt ji xj zi
we get
Δt ji
f ( u j )
u j
K
zi yk wkj
k 1
Generalised Delta Training Rule for
Multi- Layer Perceptron
f ( u j )
t ji ( n 1 ) t ji ( n ) yk wkj
zi
k 1
u j
for j 1,2 ,..., J
K
i 1,2 ,..., I
Generalised Delta Training Rule for
Multi- Layer Perceptron
Now defining the j-th column of the matrix
w11
w
21
W .
.
wK 1
w12
w22
.
.
wK 2
as
wj
. . w1J
. . w1J
. .
.
. .
.
. . wKJ
Generalised Delta Training Rule for
Multi- Layer Perceptron
and using
y1
δy .
yK
we can write
K
k 1
yk
wkj w δy
t
j
Generalised Delta Training Rule for
Multi- Layer Perceptron
In the case of bipolar activation function we
obtain for the hidden layer
f ( u j )
u j
1
2
f (1 x j )
2
'
xj
Now construct a vector whose entries are the
above terms for j=1,2,...,J, i.e.,
Generalised Delta Training Rule for
Multi- Layer Perceptron
1
2
(
x
)
1
'
1
f x1 2
' 1
2
f
x 2 ( 1 x2 )
2
'
fx
f ' 1
xJ ( 1 x 2 )
J
2
Generalised Delta Training Rule for
Multi- Layer Perceptron
and define
z1
z
2
z .
.
z I
We then have
'
t
'
yk wkj f j zi ( w j δy ) f x z
k 1
K
Generalised Delta Training Rule for
Multi- Layer Perceptron
Now defining
δx w δy f
t
j
'
x
and
t11 t12
t
21 t22
T .
.
.
.
t J 1 t J 2
. . t1I
. . t1I
. . .
. . .
. . t JI
Generalised Delta Training Rule for
Multi- Layer Perceptron
we finally obtain
T ( n 1 ) T ( n ) δx z
t
This updating formula is called the Generalised
Delta Rule for adjusting the hidden layer weights.
A similar formula was given for updating the
output layer weights:
W (n 1) W (n) δy x
t
Generalised Delta Training Rule for
Multi- Layer Perceptron
Here the main difference is in computing the error
signals y and x. In fact, the entries of y are given
as
yk
f ( vk )
( d k yk )
vk
which only contain terms belonging to the output
layer. However, this is not the case with x ,
Generalised Delta Training Rule for
Multi- Layer Perceptron
δx w δy f
t
j
'
x
f x'
whose entries are weighted sum of error
signals yk produced by the following layer.
Here we can draw the following conclusion:
The Generalised Delta Learning Rule propagates
the error back by one layer which is true for every
layer.
Generalised Delta Training Rule for
Multi- Layer Perceptron
- Summary of the Error Back-Propagation
Training Algorithm (EBPTA) Given are P
training pairs
where zi is (1 Xl), di is (K X 1), and i = 1, 2, ... ,
P. Note that the l'th component of each zi is of
value -1 since input vectors have been
augmented. Size J - 1 of the hidden layer
having outputs y is
Error Back-Propagation Training
Algorithm (EBPTA)
selected. Note that the J'th component of y is of
value -1, since hidden layer outputs have also
been augmented; y is (J X 1) and 0 is (K Xl).
Error Back-Propagation Training
Algorithm (EBPTA)
Step 1: 'T/ > 0, Emax chosen .
Weights W and V are initialized at small random
values; W is (K X J), V is (J X /).
q f-- 1, p f-- 1, E f-- 0
. Step 2: Training step starts here
(See Note 1 at end of list.)
Input is presented and the layers' outputs computed
[f(net) as in (2.3a) is used]:
Error Back-Propagation Training
Algorithm (EBPTA)
Z f-- zP' d f-- dp
Yj f-- f(vjz), for j = 1, 2, ... , J where ~'" a column
vector, is the j'th row of V, and J .
ok f-- f(w~y), . for k = 1, 2, ... , K
where Wk, a column vector, is the k'th row of W.
Step 3: Error value is computed:
1 2
E f-- '2(dk - Ok) + E, for k = 1, 2, ... , K
Error Back-Propagation Training
Algorithm (EBPTA)
Step 4: Error signal vectors 80 and 8y of
both layers are computed.
Vector 80 is (K Xl), 8y is (J X 1). (See
Note 2 at end of list.) The error signal
terms of the output layer in this step are
Error Back-Propagation Training
Algorithm (EBPTA)
1
2
Ook = -(dk- 0k)(l - Ok)' for k = 1, 2, ... , K 2
The error signal terms of the hidden layer in this step
are
12K
0yj = _ (1 - Yj) L 0okWkj, for j = 1, 2, ... , J
k=l
Step 5: Output layer weights are adjusted:
Wkj f-- Wkj + T/OokYj, for k = 1, 2, ... , K and j = 1, 2,
... ,J
Error Back-Propagation Training
Algorithm (EBPTA)
Step 6: Hidden layer weights are adjusted:
Vji f-- Vji + T/OyPi' for j = 1, 2, ... ,J and i = 1,
2, ... ,I
Step 7: If p < P then p f-- P + 1, q f-- q + 1, and
go to Step 2; otherwise, go to Step 8.
Error Back-Propagation Training
Algorithm (EBPTA)
Step 8: The training cycle is completed.
For E < Emax terminate the training session. Output
weights W, V, q, and E.
If E > Emax' then E f- 0, P f- 1, and initiate the new
training cycle by going to Step 2.
NOTE 1 For best results, patterns should be
chosen at random
from the training set Qustification follows in Section
4.5).
Error Back-Propagation Training
Algorithm (EBPTA)
11IIIII NOTE 2
If formula (2.4a) is used in Step
2, then the error
signal terms in Step 4 are computed as follows
80k = (dk - 0k)(l - 0k)ok' for k = 1, 2, ... , K K
8y) = y}(l - y) L 8okWk}' for j = 1, 2, ... , J k=l
The Hopfield Network
The Hopfield Network
We know that the Hopfield Network is a
Recurrent (Feedback or Dynamical) Neural
Network.
Let yi , i=1,2,.....,n, be the outputs of the
network and the energy function E satisfy the
following:
2
dE
dy i
i
0
dt
dt
i 1
n
where i>0 , i=1,2,.....,n.
The Hopfield Network
The above inequlity reveals that the energy
decreases with time and becomes zero if and
only if
dyi
0 i ,
dt
i.e.,
yi ( t ) cons tan t i ,
i.e.,
yi ( t ) reach their stable equilibrium states .
The Hopfield Network
Now let us assume that
1
df ( yi )
i Ci
dyi
where
Ci 0
The Hopfield Network
For the bipolar activation function
ax
1 e
y f(x)
ax
1 e
the inverse function is given by:
1 1 y
x f ( y ) ln
a 1 y
1
The Hopfield Network
The Bipolar Activation Function and its Inverse
The Hopfield Network
The Derivative of the Inverse of the Bipolar Function
dx 2 1
2
dy a 1 y
The Hopfield Network
We can conclude that
df 1( yi )
0
dyi
for
1 yi 1
Therefore
2
dE
dyi df ( yi )
Ci
0
dt
dyi
dt
i 1
n
-1
The Hopfield Network
Considering
dxi df ( yi ) df ( yi ) dyi
dt
dt
dyi
dt
-1
-1
we obtain
2
n
d
y
d
f
(
y
)
dxi dyi
dE
i
i
Ci
Ci
dt
dyi
dt dt
dt
i 1
i 1
n
-1
The Hopfield Network
Now defining
x1
x
2
x .
.
xN
y1
y
2
y .
.
y N
C diag ( Ci )
yields
t
t
dE
dy d x
dx dy
C
C
dt
dt
dt
dt dt
The Hopfield Network
Since
dE
dy
t
E( y )
dt
dt
We can write
dx
E ( y ) C
dt
This reveals that the capacitor current vector
is parallel to the negative gradient vector.
The Hopfield Network
N
dxi
wij ( y j xi ) g i xi I i
Ci
dt
j 1
wi1
y1
Ii
wi2
y2
.
.
.
yN
gi
wiN
xi
yi
Ci
N
yi f ( xi )
dxi
Ci
wij y j wij g i xi I i
dt
xi f 1( yi )
j 1
j 1
N
The Hopfield Network
Now define
N
w
j 1
ij
g i Gi
C diag ( Ci ) G diag ( Gi ), i 1,2,..., N
w11
w
12
W .
.
w1N
w12
w22
.
.
w2 N
. . w1N
. . w2 N
. .
.
. .
.
. . wNN
x1
x
2
x .
.
xN
I1
I
2
I .
.
I N
The Hopfield Network
We obtain
N
dxi
Ci
wij y j Gi xi I i
dt
j 1
consequently
dx( t )
C
Wy Gx I
dt
and since
dx
E ( y ) C
dt
The Hopfield Network
we obtain
E( y ) Wy Gx I
In the case of bipolar activation function we know that
1 1 y
x f ( y ) ln
a 1 y
1
The Hopfield Network
Therefore the state vector is given as:
1 y1
ln
1 y
1
ln 1 y2
1 1 y2
x
a
1 yN
ln 1 y
N
The Hopfield Network
We already know
N
dE
dxi dyi
Ci
dt
dt dt
i 1
therefore
N
N
dyi
dE
( wij y j Gi xi I i )
dt
dt
i 1 j 1
and
N N
dyi N
dyi N dyi
dE
( wij y j
Gi xi
Ii
)
dt
dt i 1
dt i 1 dt
i 1 j 1
The Hopfield Network
Now consider:
t
d
dy
dy
t
t
Wy y W
( y Wy )
dt
dt
dt
If
W W
t
then
t
d
dy
dy
t
t
t
( y Wy )
W y yW
dt
dt
dt
The Hopfield Network
t
t
dy
dy
dy t
dy
t
t
t
W y
Wy ( y W
) yW
dt
dt
dt
dt
Therefore
d
dy
t
t
( y Wy ) 2 y W
dt
dt
and
dy 1 d
t
yW
( y Wy )
dt 2 dt
t
The Hopfield Network
Now consider the first term of
N N
dyi N dyi
dyi N
dE
( wij y j
Gi xi
Ii
)
dt i 1
dt i 1 dt
dt
i 1 j 1
We can write:
N
N
dyi
dy
t
yW
wij y j
dt
dt
i 1 j 1
Now using the above equality, we have
N N
dyi 1 d t
wij y j
(y Wy)
dt 2 dt
i 1 j 1
The Hopfield Network
Now consider the second term in the same equation:
we can write
dyi
dyi
1
f ( yi )
xi
dt
dt
yi
d
1
f ( yi )
( f ( y )dy )
dyi 0
1
yi
yi
dyi
d
dyi d
1
1
f ( yi )
( f ( y )dy )
( f ( y )dy )
dt dyi 0
dt dt 0
1
The Hopfield Network
yi
N
N
dE
d 1 t
1
( y Wy Gi f ( yi )dy I i yi )
dt
dt 2
i 1
i 1
0
N
yi
N
1 t
1
E ( y Wy Gi f ( yi )dy I i yi )
2
i 1
i 1
0
The Hopfield Network
In order to obtain the state equations in terms
of the outputs yi consider once again
N
dxi
Ci
wij y j Gi xi I i
dt
j 1
Using
dxi 2 1
2
dyi a 1 yi
The Hopfield Network
we obtain
N
dy i
2
Ci
wij y j Gi xi I i
2
a (1 y i ) dt
j 1
and
dy i
dt
a (1 y i )
2
2Ci
N
w
j 1
ij
y j Gi xi I i
The Hopfield Network
a( 1 y )
dy
1
Wy GΓ (y) I
diag
dt
2Ci
2
i
The Hopfield Network
g12 g11
x1
g1
y1
C1
dx1
g1 x1 C1
g11 ( y1 x1 )+ g12 ( y2 x1 )
dt
g21
g22
g2
x2
y2
C2
dx2
g 2 x2 C2
g 22 ( y2 x2 )+g 21 ( y1 x2 )
dt
The Hopfield Network
C1
0
dx1
0 dt g11
C1 dx2 g 21
dt
g12 y1 g1 g11 g12
0
g 22 y2
0
x1
g 2 g 22 g 21 x2
which yields
C1 0
g11
C
, W
0 C1
g 21
g12
g1 g11 g12
, G
g 22
0
0
g 2 g 22 g 21
and
1
E y1
2
The Hopfield Network
g11
y 2
g 21
g11
E ( y1 , y2 )
g 21
yi
g12 y1
1
Gi f y dy
g 22 y2 i1 0
2
g12 y1 1 G1
g 22 y2 a 0
1 y1
ln
0 1 y1
G2 1 y2
ln 1 y
2
The Hopfield Network
and
1
1 y1
E
y g11 y1 g12 y2 a G1 ln 1 y
1
1
E ( y1 , y2 )
1
1 y2
E
y g 22 y1 g 21 y1 a G2 ln 1 y
2
2
The Hopfield Network
y
y
1
2
1
2
2
1
E ( g11 y1 g 22 y2 y1 y2 g12 y1 y2 g12 ) G1 f y dy G2 f 1 y dy
2
0
0
y
y
2
1
1 1 1 y
1 y
2
2
E ( g11 y1 g 22 y2 y1 y2 g 21 y1 y2 g12 ) G1 ln
dy G2 ln
dy
2
a 0 1 y
1 y
0
Now consider
yi
yi
yi
1 y
I ln
dy ln( 1 y )dy ln( 1 y )dy
1 y
0
0
0
The Hopfield Network
and
yi
I1 ln( 1 y )dy
0
Let
Hence
ln( 1 y ) u
1 y v
then
dy
du
1 y
dv dy
yi
yi
yi
0
0
0
I1 ln( 1 y )dy udv ( uv ]0yi vdu )
yi
dy
{ ln ( 1 y )}( 1 y )] ( 1 y )
1 y
0
yi
0
The Hopfield Network
I1 { ln ( 1 yi )}( 1 yi ) yi
I 2 {ln ( 1 yi )}( 1 yi ) yi
yi
yi
yi
1 y
I ln
dy ln( 1 y )dy ln( 1 y )dy
1 y
0
0
0
I I1 I 2 { ln ( 1 yi )}( 1 yi ) {ln ( 1 yi )}( 1 yi )
The Hopfield Network
The Hopfield Network
y
y
2
1
1 1 1 y
1
1 y
2
2
E ( g11 y1 g 22 y2 y1 y2 g12 y1 y2 g12 ) G1 ln
dy G2 ln
dy
a 0 1 y
a 0 1 y
2
1
1
E {g11 y12 g 22 y22 (g12 g 21 )y1 y2 } G1 ( 1 y1 ) ln( 1 y1 ) ( 1 y1 ) ln( 1 y1 )
a
2
1
G2 ( 1 y2 ) ln( 1 y2 ) ( 1 y2 ) ln( 1 y2 )
a
The Hopfield Network
The Hopfield Network
The Hopfield Network
The Hopfield Network
The Hopfield Network
Using
The Hopfield Network
a( 1 yi2 )
dy
1
diag
Wy GΓ (y) I
dt
2Ci
the state equations are obtained as
2
y
1
1
dy1 a
dt 2C1
dy2 0
dt
1 1 y1
0
ln
a
1
y
g
g
y
G
0
1
12
1
1
11
1 y22 g 21 g 22 y2 0 G2 1 1 y2
a
a ln 1 y
2C2
2
dy1 1 (1 y 2 )(ag y ag y G ln 1 y1 )
1
11 1
12 2
1
dt 2C1
1 y1
dy2 1 (1 y 2 )(ag y ag y G ln 1 y2 )
2
22 2
21 1
2
dt 2C2
1 y2
Discrete-Time Hopfield Networks
Consider the state equation of the Gradient-Type
Hopfield Network:
dx( t )
C
Wy Gx I
dt
We can write
dx( t )
-1
C
Wy GΓ (y) I
dt
Discrete-Time Hopfield Networks
As the plot of the inverse
bipolar activation function
shows the second term in
the above equation is zero
for high gain neurons.
Hence:
dx( t )
C
Wy I
dt
Discrete-Time Hopfield Networks
Now consider
dxi df ( yi ) df ( yi ) dyi
dt
dt
dyi
dt
-1
Using the this plot we
can conclude that
df -1 ( yi )
0
dyi
for high gain neurons.
-1
Discrete-Time Hopfield Networks
Hence
dx( t )
0
dt
It follows that
0 Wy I
Now let us solve this equation using Jacobi’s
algorithm. To this end define:
Discrete-Time Hopfield Networks
where
W' W D = L U
L,U and D = diag( wii )
Are the lower and upper triangular and diagonal
matrices shown in the following decomposition
of W.
W
w11
w
21
.
.
w N1
w12
w 22
.
.
w N2
.
.
.
.
.
. w1N w11
. w 2N 0
.
. .
.
. .
. w NN 0
0
w 22
.
.
0
.
.
.
.
.
0
.
0 0
0
.
0 w 21
.
. w 31 w 32
.
.
. .
. w NN w N1 w N2
.
.
0
.
.
.
.
.
.
w N,N1
0 0 w12
0 0
0
..
.
. .
.
0 0
0
.
.
.
.
.
. w1N
. w 2N
.
.
. w N1,N
.
0
Discrete-Time Hopfield Networks
Now defining
we obtain
D diag( wii )
-Dy = W'y + I
-1
-1
y = -D W'y - D I
Now define
-D W' = W
-1
-D I I
-1
Discrete-Time Hopfield Networks
y = Wy I
Now replace the vector y on the right-hand side
by an initial y(0) vector. If the vector y on the lefthand side is obtained as y(0), then y(0) is the
solution of the system. If not then call the vector y
obtained on the left-hand side y(1), i.e.,
Discrete-Time Hopfield Networks
y(1) = W y(0) I
and in general we can write
y(k + 1) = W y(k) I
Discrete-Time Hopfield Networks
The method will always converge if the matrix
W is strictly or irreducibly diagonally
dominant. Strict row diagonal dominance
means that for each row, the absolute value of
the diagonal term is greater than the sum of
absolute values of other terms:
wii wij
i j
Discrete-Time Hopfield Networks
The Jacobi method sometimes converges even
if this condition is not satisfied. It is necessary,
however, that the diagonal terms in the matrix
are greater (in magnitude) than the other
terms.
Discrete-Time Hopfield Networks
Solution by Gauss-Seidel Method
In Jacobi’s method the updating of the
unknowns is made after all N unknowns have
been moved to the left side of the equation. We
will see in the following that this is not
necessary, i.e., the updating can be made
individually for each unknown and this updated
value can be used in the next equation. This is
shown in the following equations:
Discrete-Time Hopfield Networks
x1 (n 1)
x2 (n 1)
1
a21x1 (n 1) a23 x3 (n) ..... a2 N xN (n) b2 a22
a22
x3 ( n 1)
and
1
[ a12 x2 (n) a13 x3 (n) ...... a1N xN (n) b1 ]
a11
1
a31x1 (n 1) a32 x2 (n 1) a34 x2 (n) ...... a3 N xN (n) b3 a33
a33
xN (n 1)
1
aN 1 x1 ( n 1) aN 2 x2 ( n 1) ...... aN , N 1 xN 1 ( n 1) bN aNN
aNN
In vector-matrix form, we can write:
D x (n 1) L x (n 1) U x (n) b
( D L) x (n 1) U x (n) b
x (n 1) ( D L) 1 (U x (n) b)
Discrete-Time Hopfield Networks
This matrix expression is mainly used to analyze
the method. When implementing Gauss Seidel,
an explicit entry-by-entry approach is used:
1
xi (n 1)
aii
bi aij x j (n 1) aij x j (n)
j i
j i
Discrete-Time Hopfield Networks
Gauss-Seidel method is defined on matrices with non-zero
diagonals, but convergence is only guaranteed if the matrix
is either:
1. diagonally dominant or
2. symmetric and positive definite.