* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download search for quantum gyroscopes - Ohio University Physics and
State of matter wikipedia , lookup
Lorentz force wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
Field (physics) wikipedia , lookup
Time in physics wikipedia , lookup
Magnetic field wikipedia , lookup
Hydrogen atom wikipedia , lookup
Old quantum theory wikipedia , lookup
Photon polarization wikipedia , lookup
EPR paradox wikipedia , lookup
History of quantum field theory wikipedia , lookup
Bell's theorem wikipedia , lookup
Electromagnetism wikipedia , lookup
Magnetic monopole wikipedia , lookup
Quantum vacuum thruster wikipedia , lookup
Neutron magnetic moment wikipedia , lookup
Electromagnet wikipedia , lookup
Superconductivity wikipedia , lookup
Spin (physics) wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
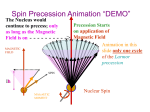
SEARCH FOR QUANTUM GYROSCOPES Abhishek Singh Visen 032, Clippinger Physics Lab, Ohio University, Athens, OH 45701. [email protected] Abstract: This paper is primarily a review of developments in Quantum Mechanics pertaining to spin related phenomena so far, with particular emphasis on exploring gyroscopic effects in the published spin related papers. The paper indeed aims at exposing the existing vacuum in the incipient field of Rotational Quantum Dynamics – which possesses the potential to generate dramatic quantum phenomena. The paper begins with exposing the ongoing misinterpretation of Stern-Gerlach experiment[1]. Then the paper exhaustively explores reported spin-precessions. The paper also indulges into an interesting discussion “impossibility of arbitral flip” of electrons. Attempts will be made to explore gyroscopic effects in scattering of the particles, explain geo-magnetism and bio-chirality, peculiar torque experienced by magnets etc.. Keywords: Stern-Gerlach, Spin precession, Larmour Precession, Thomas precession I. Spin Precession This part of the paper primarily aims at analyzing various spin related precessions to arrive at vital conclusion of : “Quantization of spin precession” or “impossibility of existence of arbitral flip” (which has been pompously used in the JJ Sakurai text), which may have dramatic influence on our way of notion of spin and may give cosmic background / relicit radiation style avenue for exploration of bigbang. Before I begin let me reveal what Quantization of angular momentum during flip is : It states that “when even a flip occurs then the angular momentum is nћ”. Let’s begin with precession of classical charged sphere in a magnetic field. Assuming that at time t = 0, there is no magnetic field but a charged sphere is spinning in space with spin pointing towards positive êx axis. Then the inertia tensor is given by: Since the matrix is already digitalized, the kinetic energy of the sphere is given by: 1/5 MR2 ωx2 If the sphere is having charge q, then the magnetic moment of sphere is given by: 1/3 QωR2 As the magnetic field is switched on in êz direction then, the top instead of acquiring minimum electromagnetic energy configuration (i.e., magnetic moment aligned with the magnetic field), however, the sphere precesses under the effect of gyroscopic torque which is proportional to (Ix - Iy) ωxωz. This phenomena is not very lucidly understood. However the rate of precession is: ω = -qB/2m = γB where, γ is gyro-magnetic ratio Such precessions are referred as Larmor precession. Such precessions are now converted into technology. MRI, Paramagnetic Resonance, Ferromagnetic resonances (Liftshift & Landau) are fantastic manifestations of Larmor precession. Now let’s come on to the quantum mechanical version of precession. Actually JJ Sakurai (revised edition) contains over generalized description of spin precession. Actually, as the electron is in the magnetic field, with its spin inclined to angle θ is given by: hS1(t)i = While Larmor frequency is given by: Now it can be seen that precession does depends upon orientation of the particle with the magnetic field. The (possible) dependence of Hamiltonians on the angle of inclination may have important technological importance. Actually, such precession has been aptly applied for various technological purposes like: MRI, NMR, ESR etc.. II. Semi-classical explanation of Stern-Gerlach experiment Usually Stern-Gerlach experiment is thought of as ‘bizarre’ Quantum Mechanical phenomena. In the following lines attempts are made to re-interpret is semi-classically. (space left) III. Quantization of Precession For proper understanding of quantum phenomena, I think following should be enunciated as established principles: 1. For a fermionic system, the spin precession is quantized. 2. It is impossible to have any stable state other than eigen-values of the Fermion. Above principles can help us in understanding various phenomena like: 1. 2. 3. 4. 5. Nuclear Magnetic Resonance ESR Magnetic Resonance Imaging Precession clocks Ferromagnetic resonances etc.. IV. Trajectory of the precessing electrons The classically predicted trajectory of electron ignores the interaction of the spin of the electron with the magnetic field. More elaborate studies of trajectories of electrons in magnetic field is required. V. Certain Gyroscopic experiments There are certain gyroscopic experiments which I want to propose. These experiments are very simple and affordable, but are important because they offer a unique synergy of classical and quantum mechanics. a) Torque on a magnetic bar: If we take a magnetic bar and an iron bar of same dimensions, and rotate them. The magnetic bar will experience a torque. This is because, there are magnetic moments inside the magnets, which when rotated will generate an torque. For first initial estimate. Assuming about 1023 atoms/cm3 are inclined in a same direction. Then the approximate torque is given by: τ ≈ ω me r2 (1015) * 1023 ≈ 10-3 (This calculation may be wrong) b) Demagnetization of magnet bar: Using the gyroscopic torque the magnet can be demagnetized by revolving it. c) Magnetization of rotating fluid: It is predicted that molten metals can be magnetized by rotating it. This may be the cause of earth’s magnetism. VI. Conclusions On the whole it can be seen that there are many interesting unexplored territories in the field of quantum gyroscopes. Interest in this area will enable mankind to search for vital truths about the nature. References 1. [Peniaz] 1978 2. Phys Rev Lett. 1986 Nov 17;57(20):2500-2503 3. Morton, Jr., S. Harold, 1993, Hamiltonian and Lagrangian Formulations of Rigid Body Rotational Dynamics Based on Euler Parameters, J. Astronaut. Sci., 41, pp. 561–5991. 4. S. V. Vonsovskii, Ferromagnetic Resonance (Pergamon: Oxford, 1966). 5. S. Chikazumi, Physics of Ferromagnetism (Oxford: New York, 1996). 6. http://nobelprize.org/nobel_prizes/physics/laureates/2006/phyadv06.pdf