Download Study notes for - hrsbstaff.ednet.ns.ca

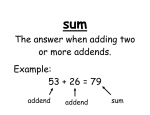
Study notes for:
WHOLE NUMBERS
PLACE VALUE OF WHOLE NUMBERS
Numbers are written using the digits 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. The placement of these digits in
any number determines the meaning and value of the number.
In the number 597 and 851, the fives look the same (face value) but the place value is different.
597 -+ the '5' in this number means that we have 5 hundreds
851 -+ the '5' in this number means that we have 5 tens
The value of each digit of a number written in standard form can be expressed when we write the
number in expanded form.
The number 834 576 expressed in various forms is as follows:
Standard Form: 834 576
Expanded Form: (8 x 100000) + (3 x 10 000) + (4 x 1000) + (5 x 100) + (7 x 10) + (6 x 1)
Word Form: eight hundred thirty-four thousand, five hundred seventy-six
GRAPHING WHOLE NUMBERS
We can graphically represent any sets of whole numbers if we are given certain conditions that must be
met. The examples below show how this is done.
EXAMPLE #
1: Graph the set of natural numbers less than 5.
EXAMPLE #2: Graph the set of whole numbers greater than 3.
EXAMPLE # 3: Graph the set of whole numbers greater than 2 but less than 6.
RQUNNING_&_ESTIMATION WITH WHOLE_NUMBRRS
Often, when using mathematics, an estimate will suffice as opposed to an actual calculation. To
estimate an answer we usually round off first, then calculate with numbers that are easier to
work with. The examples below show how to round off numbers and then how to estimate your answer.
EXAMPLE # 1 Round 3274 to the nearest ten.
3274 becomes 3270
The '7' is in the tens place. If the number behind the '7' is a 5 or larger, the '7' becomes an '8'.
Otherwise it stays the same as it did in this case.
EXAMPLE #.2 Round 42 938 to the nearest thousand.
42 938 becomes 43 000
The '2' is in the thousands place. If the number behind the '2' is a 5 or larger, the '2' becomes
a '3'. Otherwise it would have stayed the same.
EXAMPLE #3: The area of New Brunswick is 73 436 km2. In 1979 its population was 699 920.
Approximately how many people per square kilometre (km2) were there in N.B. in 1979?
Actual_ 699 920 + 73 436 = ?
Approximate: 700 000 + 70 000 = 10
:. there were approximately 10 peoplejkm2 in N.R in 1979.
ADDITION AND SUBTRACTION OF WHOLE NUMBERS
Whenever you add or subtract whole numbers, you must remember to line up the numbers that have the
same place value. (The tens under the tens, the thousands under the thousands, the hundreds under the
hundreds and so on, as shown in the examples below.)
EXAMPLE fi Calculate the sum of 4152,965 and 2876.
ESTIMATE
ACTUAL
4000 addend
4152
addend
+1000 addend
+3000 addend
8000 SUM
+ 965
+2876
7993
addend
addend
SUM
EXAMPLE it2: Calculate the difference between 5784 and 2239.
ESTIMATE
5800
-2200
3600
minuend
subtrahend
DIFFERENCE
ACTUAL
5784 minuend
-2239 subtrahend
3545 DIFFERENCE
MULTIPLICATION AND DIVISION OF WHOLE NUMBERS
Unlike addition or subtraction, you do
not have to line up the numbers that have the same
place value when performing the operations of multiplication or division.
The examples below show how multiplication and division is done.
EXAMPLE # 1 Calculate the product of 47 and 104.
ACTUAL
ESTIMATE
100
x50
5000
multiplicand
multiplier
PRODUCT
104
X 47
728
4160
4888
multiplicand
multiplier
PRODUCT
EXAMPLE #2 Calculate the quotient when 1462 is divided by 28.
ESTIMATE
50
divisor 30) 1500
1500
0
QUOTIENT
dividend
remainder
ACTUAL
52 QUOTIENT
28) 1462 dividend
140x
62
56
6
remainder
ORDER OF OPERATIONS (BEDMAS)
B
E
D
M
A
S
BRACKETS
EXPONENTS
DMDE
MULTIPLY
ADD
SUBTRACT
The chart above shows the order in which operations must be completed when doing a
question that has more than one operation. The examples below show the correct procedure
you must use when calculating number
1. If addition and subtraction occur in the
4. If multiplication, division, addition, or
same expression, perform the operations
subtraction occur together, first perform
in the order in which they occur.
the multiplication and division in the
expressions.
order they occur and then perform the
addition and subtraction last.
EXAMPLE:_
21 + 4 - 5 + 3
'"
25 -5+3
EXAMPLE:
20 + 3 = 23
10 x 4+8+9
40 + 8 + 9
2. If multiplication and addition or
5 + 9 = 14
subtraction occur together, perform
5. If brackets occur in a number
the operation of multiplication first.
expression, perform whatever operation is
enclosed in brackets first, then follow the
EXAMPLE: 24 + 5 x 4 - 2 x 3 + 8
rules above.
24 + 20 - 6 + 8
EXAMPLE: 12 ./. (7 - 4) x 5
44 -_ +8
12 ./.3 x . 5
38 + 8 = 46
4
x 5 = 20
3. If division and addition or
subtraction occur together, perform the
6. If line such as we use in division or
operation of division first.
fractions occurs in a number expression,
evaluate the numerator (top part) and
EXAMPLE_ 19 + 16 ./. 4 - 5
denominator (bottom part) before
19 + 3 - 5
dividing.
23 - 5 = 18
EXAMPLE: 8 x 4 + 3 = 35 = 5
1+3 x 2
7
SUBSTITUTION
Symbols or letters are sometimes used as replacements for numbers in an expression. To
calculate the value of the expression we substitute numbers for the symbols or letters and
solve each by using the rules for order of operations (BEDMAS) as shown in the examples
below.
EXAMPLE #1
EXAMPLE #2
Evaluate the expression below if:
Evaluate the expression below if:
0 = 5 and 0 = 2
3xO-4xO
3x5-4x2
15 - 8 = 7
a=3andb=2
5ab + 4a - 10
5 x 3 x2 + 4 x 3 - 10
30
+ 12 - 10
PROPERTIES OF WHOLE NUMBERS
= 32
The chart below illustrates some of the properties of whole numbers showing us what we
can do and what we cannot do when we add, subtract, multiply or divide.
PROPERTIES OF WHOLE NUMBERS
Property
1. Commutative
Property
2. Associative
Property
Addition
Subtraction
Multiplication
12+2=2+1Z
9-5"5-9
does not work
5x9=9x5
(8+ 5) + 3=8+ (5 + 3)
(9-7)-4 " 9-(7-4)
does not work
20+5"5+20
does not work
(5x3)x2 = 5x(3x2)
3. Identity
Element
0+13=13
(Zero is the I.E.)
4. Division
by ZERO
IIIIIIIIIIIIII IIIIIIIIIIIIII IIIIIIIIIIIIII
5. Zero
Property
IIIIIIIIIIIIII IIIIIIIIIIIIII
7-0=7
(Zero is the I.E.)
19 x 1 = 19
(One is the I.E.)
47
x0
Division
=0
(8+4)+2 "8+(4+2)
does not work
25+1=25
(One is the I.E.)
35 + 0
=?
This is impossible,
or undefined
IIIIIIIIIIIIII
WHOLE NUMBERS REVIEW
What is the place value of the '7' in each?
1. 734
2. 3471
3. 80 007
B. Graph each of the following.
1. All whole numbers greater than 8.
4. 173 483
2. All the even whole numbers.
C. Round each to the place indicated.
1. 5634 (tens) 2. 478 (thousands) 3. 92999 (tens)
4. 87 924 (hundreds)
D. Calculate the missing value of each.
1. 426 +
= 763
2. 4596 - 386 =
3. 1456 + 7 =
4. 83 x 752 =
5.
6. 53 + 861 + 234 =
7. 986 +
8. 562 - 47 =
+ 27 = 1096
x 62 = 3286
9. 352 -
= 96
10. 93 x 68 =
11. 786 + 25 = 31 R
12. 876 + 35=
13. 476 = 984 –
14. (62)(35) =
15. 63 + 42 +
16. (86)(
17. (9 + 18) - 3 =
18. 986 +
20.
21. 965 + 18 =
19. 3 x 5 x
) = 10 664
= 180
+ 16 = 19 R4
= 346
= 28 R6
E. Write the next 4 terms for the following sequences.
1. 1, 2, 3, 4,
2. 2, 4, 8, 16,
3. 1, 5, 9, 13,
4. 14, 17, 20, 23,
5. 7, 14, 21, 28, --6. 6. 2, 3, 5, 8, 12, 17,
7.
8.
9.
7. 1, 4, 9, 16, 25,
8. 2, 3, 5, 8, 13, 21,
9. 0, 3, 8, 15, 24,
10. 2, 5, 10, 17,
F. Write each in expanded form.
1. 563
2. 40 003
3. 76 010
4. 90 301
G. Evaluate each of the following using the order of operations rules.
1. 4 x (9 - 5) + 16 + 4
3. (49 + 7) x (56 + 8)
5. 3x + 2x, if x = 4
7. 2y- y + (y + 5), if y = 12
9. t + 2t if t = 5
t
11. xy + 3x – 2y, if x = 4, y = 5
13. z(w – 4), if w=4 , z = 6
15. mn + m² + n² , if m = 2 , n = 1
17. y² - y +6, if y = 4
19. (mn) - (3h), if m = 5, n = 2
21. (P)(q)(P)(q), if p = 3, q = 4
23. (6 + q) + (8 + r), if q = 3, r = 4
2. (8 - 2) x (4 + 3) x (10 - 6)
4. 13 - 2 x 6 + 4
28/7-3
6. (4+9) x 2
28/7-3
8. (a + 3) + (2a), if a = 3
10. 2m + 4m2 + 5 - 15, if m = 2
12. n2 + 2g, if n = 3, g = 4
14. (3a - b)(a + 3b), if a = 2, b = 3
16. x + 2y, if x = 1, Y = 4
18. y² + z - 6 + 2z, if y = 4, z = 2
20. m + n, if m = 6, n = 4
m-n
22. 3w - z, if w = z = 8
24. 5a - ab + 7, if a = 5, b = 3