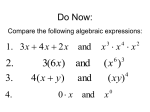Download ELEMENTS OF ALGEBRA III

ELEMENTS OF ALGEBRA III
(P. 1 – P.3 STUDY GUIDE)
SETS – we use the following to characterize numbers with similar characteristics

Real numbers – all rational and irrational numbers

Rational numbers – all terminating or repeating decimals and/or fractions
i.e. ½, 2, .333333….., ¾

Irrational numbers – all non-terminating, non-repeating decimals…these numbers
cannot be written as a fraction
i.e. Pie, .12122122212222….

Integers – this set includes all positive and negative numbers including “0” but
excluding all fractions and decimals
i.e. {…-2, -1, 0, 1, 2,…}

Natural numbers – this set includes all positive numbers only
i.e. {1, 2, 3, ….}

Prime numbers – can only be divided by 1 and itself
i.e. {1, 2, 3, 5, 7, 11, …}

Composite numbers – these numbers are divisible by more numbers than just 1
and itself
i.e. {4, 6, 8, 10, …}
SET BUILDER NOTATION -> {x l ……..}

Element – each member of a set is known as this
i.e. {2, 3, 5} – 2, 3, 5 are each elements of this set

Subset – if every element of some set “A” is also an element of “B,” than “A” is
considered a subset of “B.”
i.e. The set of negative integers is a subset of the set of integers

Empty Set (null-set) – set that contains no elements

Infinite Set – all the elements of the set cannot be listed
i.e. The set of Real numbers
UNION & INTERSECTION

Union – a union of 2 sets (A U B) is the set of all elements that belong to
EITHER “A” OR “B”
i.e. A U B = {x l x <- A OR x <- B}

Intersection – an intersection of 2 sets (A  B) is the set of all elements that
belong to BOTH “A” AND “B.” Look for what these sets have in common.
i.e. A  B = {x l x <- A AND x <- B}
ABSOLUTE VALUE & DISTANCE

Absolute value – the absolute value of a real number “a,” is the distance between
“a” and “0” on the number line.
i.e. The absolute value of 3 is 3 and the absolute value of -3 is 3…Both
numbers are the same distance from “0” on the number line

How to find the distance between two points on a number line “A” and “B:”
d = a b
d (-2, 5) =  2  5 =  7 = 7
INTERVAL NOTATION
i.e. (-4, 3] U [1, 5)
(
)
Means end points are not included -> Open
[
]
Means end points are included -> Closed
[
)
Means right hand number is included and left hand number is
Not
(
]
Means right hand number is not included and left hand number
is
Examples:
(2,
)
_______________________________________
(- , 3]
_______________________________________
(- , -2] U (3, )
_______________________________________
EVALUATE

Solve these problems by simply substituting in the given values into the given
equation…REMEMBER to follow the order of operations PEMDAS
i.e.
x = 2 y = -3
8  27
35
x3  y3
2 3  (3) 3
=
=
=
=5
2
2
2
2
469
7
x  xy  y
2  2(3)  (3)
PROPERTIES










Closure
Commutative
Associative
Identity
Inverse
Distributive
Reflexive
Symmetric
Transitive
Substitution
RULES OF EXPONENTS

Same Base, add the exponents
i.e.

1.)
x3  x4  x7
2.)
2 5  2 7  212
When raising from a power (exponent) to a power (exponent), multiply
exponents
i.e.

1.)
(x3 )3  x9
2.)
(2 2 ) 4  2 8
When dividing using exponents, you must subtract the exponents
i.e.

1.)
x5
 x2
3
x
2.)
x3
1
 2
5
x
x
3.)
16 x 3 y 5 z 4 4 y 3 z 3

4x 7 y 2 z
x4
When given negative exponents, change its location to make it positive
i.e.
1.)
x 5
1
1
 7
 12
7
5
x
x x
x
SCIENTIFIC NOTATION

We use scientific notation to write really large or small numbers

The new number “n”, must be greater (>) than “0”, but less than or equal  
to “1”

Exponent is positive when it is a large number
i.e.
765,000,000 = 7.65  10 8

Exponent is negative when it is a small number
i.e.
.000045 = 4.5  10 5

We can also use scientific notation to simplify word problems
i.e.
1.4  1019 1.4

 10 7  0.5  10 7  5  10 6
12
2.8
2.8  10
RATIONAL EXPONENTS

In order to solve these problems follow this example:
a
x
y
x = power you are raising to
y = index/root
i.e.
1
2
9  9 3
i.e.
643
2

 64 
2
3
 4  16
2
i.e.
4
3
8 
 8
4
3
 2  16
4
i.e.
6
32 5

1
32
6
5

1
 32 
5
6

1
2
6

1
32
*NOTE: MAKE NEGATIVE EXPONENTS POSITIVE FIRST*
SIMPLIFYING EXPONENTS (Absolute Value Needed when Even, Even, Odd)

The same rules for exponents apply concerning, product, quotient, and
powers.
i.e.
1
2
5
2
1
2
5
2
 x y 
x 
x
x
 3 5    2   2 
y
x y 
y 
y2
2
3
5
i.e.
1
5
1



  5 x 3   4 x 2   20 x 6







REMEMBER the following:
x2  x
n
bn  b
when n is even
n
bn  b
when n is odd
4
16 z 4  2 z  2 z
5
32a 5  2a a does not get an absolute value because it has an
odd exponent
i.e.
z gets an absolute value because it has even
exponent…Even (root), Even (Power), Odd
(Answer)
i.e.
PROPERTIES OF RADICALS

Product Property
n


a  n b  n ab
Quotient Property
n
a
n
b
n
a
b
The index (n) must be identical in order to divide
Index Property
m n

The index (n) must be identical in order to multiply
a  m n a
Adding/Subtracting
2 x 3 x 5 x

Must have the same radicand and index in order to
perform operation
Examples:
A.)
4
32 x 3 y 4  2 y 4 x 3
NOTE: Not enough x’s to pull out…Need 4
or more to remove from under radical
B.) 5x3 16 x 4  3 128x 7  5x3 2 4 x 4  3 2 7 x 7  5x2 x 3 2 x  2 2 x 2 3 2 x
= 10 x 2 3 2 x  4 x 2 3 2 x
= 6x 2 3 2x
C.)


3 6  2 10  18  2 30  3 2  2 30
RATIONALIZE THE DENOMINATOR

REMEMBER: When dealing with radicals you can never have a radical in the
denominator
i.e.
5
2
2

2

5 2
4

5 2
2
i.e.
5
3
a

3
a2
3
a2

53 a 2
3
a3

53 a 2
a
i.e.
2
3 2
NOTE: If we have addition or subtraction and a
radical in the denominator we multiply by the
conjugate…If subtraction the conjugate would be
addition, and if addition than the conjugate would
be subtraction (only the sign changes).
2
3 2

3 2
3 2

2 32 2
9 6 6 4

2 32 2
 2 32 2
32