Download Last Time… - UW-Madison Department of Physics

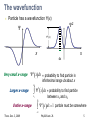
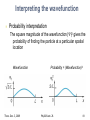
Exam 3 covers
Lecture, Readings, Discussion, HW, Lab
Exam 3 is tonight, Thurs. Dec. 3, 5:30-7 pm, 145 Birge
Magnetic dipoles, dipole moments, and torque
Magnetic flux, Faraday effect, Lenz’ law
Inductors, inductor circuits
Electromagnetic waves:
Wavelength, freq, speed
E&B fields, intensity, power, radiation pressure
Polarization
Modern Physics (quantum mechanics)
Photons & photoelectric effect
Bohr atom: Energy levels, absorbing & emitting photons
Uncertainty principle
Thurs. Dec. 3, 2009
Phy208 Lect. 26
1
From Last time…
De Broglie wavelength
Uncertainty principle
Wavefunction of a particle
Spatial extent of ‘wave
packet’
x
• x = spatial spread of ‘wave packet’
• Spatial extent decreases as the spread in
included wavelengths increases.
Thurs. Dec. 3, 2009
Phy208 Lect. 26
3
Wavefunction
• Quantify this by giving a physical meaning to
the wave that describing the particle.
• This wave is called the wavefunction.
– Cannot be experimentally measured!
• But the square of the wavefunction is a
physical quantity.
– It’s value at some point in space
is the probability of finding the particle there!
Thurs. Dec. 3, 2009
Phy208 Lect. 26
4
The wavefunction

Particle has a wavefunction (x)
2

2(x)
x
dx
Very small x-range
x
2 xdx = probability to find particle in
infinitesimal range dx about x
x2
Larger x-range

Entire x-range
  xdx = probability to find particle
2
x1


between x1 and x2
 2 x dx  1 particle must be somewhere

Thurs. Dec. 3, 2009
Phy208 Lect. 26
5
Probability
Probability
0.5
P(heads)=0.5
P(tails)=0.5
0.0
Heads
Tails
Probability
P heads  P tails  1
0.5

P(1)=1/6
P(2)=1/6
1/6
0.0
etc
1 2 3 4 5 6
P 1  P 2  P 3  P 4   P 5  P 6  1
Thurs. Dec. 3, 2009
Phy208 Lect. 26
6
Discrete vs continuous
6-sided die, unequal prob
0.5
1/6
0.0


Loaded die
Infinite-sided die, all
numbers between 1 and 6
“Continuous” probability
distribution
1 2 3 4 5 6
0.5
P(x)
Probability

6

 P(x)dx  1
0.0
0 1 2 3 4
x
1
Thurs. Dec. 3, 2009
1/6
Phy208 Lect. 26
5 6
7
Example wavefunction


What is P(-2<x<-1)?

1
2

 xdx = fractional area under curve -2 < x < -1
2

2
= 1/8 total area -> P = 0.125
What is (0)?

2

 xdx = entire area under 2 curve = 1

= (1/2)(base)(height)=22(0)=1  0 1/ 2
Thurs. Dec. 3, 2009
Phy208 Lect. 26
8
Wavefunctions

Each quantum state has different wavefunction
Wavefunction shape determined by physical
characteristics of system.

Different quantum mechanical systems




Pendulum (harmonic oscillator)
Hydrogen atom
Particle in a box
Each has differently shaped wavefunctions
Thurs. Dec. 3, 2009
Phy208 Lect. 26
9
Quantum ‘Particle in a box’
Particle confined to a fixed region of space
e.g. ball in a tube- ball moves only along length L
L

Classically, ball bounces back and forth in tube.

A classical ‘state’ of the ball.

State indexed by speed,
momentum=(mass)x(speed), or kinetic energy.

Classical: any momentum, energy is possible.
Quantum: momenta, energy are quantized
Thurs. Dec. 3, 2009
Phy208 Lect. 26
10
Classical vs Quantum
Classical: particle bounces back and forth.


Sometimes velocity is to left, sometimes to right
L

Quantum mechanics:



Particle represented by wave: p = mv = h / 
Different motions: waves traveling left and right
Quantum wavefunction:

superposition of both at same time
Thurs. Dec. 3, 2009
Phy208 Lect. 26
11
Quantum version


Quantum state is both velocities at the same time
Superposition waves is standing wave,
made equally of



Wave traveling right ( p = +h/ )
Wave traveling left ( p = - h/ )
Determined by standing wave condition L=n(/2) :
  2L
One halfwavelength
L
Quantum wave function:
superposition of both motions.
Thurs. Dec. 3, 2009
momentum
h h
p 
 2L
Phy208 Lect. 26
2 2 
 x  
sin  x 
L   

12

Different quantum states

p = mv = h / 


Different speeds correspond to different 
subject to standing wave condition
integer number of half-wavelengths fit in the tube.
  2L /n
  2L
n=1 One
halfwavelength
n=2
L
Two halfwavelengths
Thurs. Dec. 3, 2009
2  2 
sin n
x 
Wavefunction:  x  
L   
momentum
h h
p 
 po
 2L
n=1

n=2
Phy208 Lect. 26

momentum
h h
p    2 po
 L
13
Particle in box question
A particle in a box has a mass m.
Its energy is all kinetic = p2/2m.
Just saw that momentum in state n is npo.
It’s energy levels
A. are equally spaced everywhere
B. get farther apart at higher energy
C. get closer together at higher energy.
Thurs. Dec. 3, 2009
Phy208 Lect. 26
14
Particle in box energy levels
Quantized momentum
h
h
p n
 npo

2L
 Energy = kinetic
2
2
npo 
p

E

 n2Eo

2m
2m


Or Quantized Energy
Energy

n=5
n=4
En  n2Eo
n=3
n=quantum number
n=2
n=1
Thurs. Dec. 3, 2009
Phy208 Lect. 26
15
Zero-point motion


Lowest energy is not zero
Confined quantum particle cannot be at rest


Always some motion
Consequency of uncertainty principle xp  /2



p cannot be zero
p not exactly known
p cannot be exactly zero
Thurs. Dec. 3, 2009

Phy208 Lect. 26
16
Question
A particle is in a particular quantum state in a box of length L.
The box is now squeezed to a shorter length, L/2.
The particle remains in the same quantum state.
The energy of the particle is now
A. 2 times bigger
B. 2 times smaller
C. 4 times bigger
D. 4 times smaller
E. unchanged
Thurs. Dec. 3, 2009
Phy208 Lect. 26
17
Quantum dot: particle in 3D box
CdSe quantum dots
dispersed in hexane
(Bawendi group, MIT)
Color from photon
absorption
Decreasing particle size


Determined by energylevel spacing
Energy level spacing increases
as particle size decreases.
i.e
2
E n 1  E n
Thurs. Dec. 3, 2009
n  1 h 2 n 2 h 2



8mL2
8mL2
Phy208 Lect. 26
18
Interpreting the wavefunction

Probability interpretation
The square magnitude of the wavefunction ||2 gives the
probability of finding the particle at a particular spatial
location
Wavefunction
Thurs. Dec. 3, 2009
Probability = (Wavefunction)2
Phy208 Lect. 26
19
Higher energy wave functions
L
n
p
n=3
h
3
2L
E
Probability
2
h
32
8mL2
n=2  2 h
2L
h2
2
8mL2
 h
2L
h2
8mL2
 n=1
Wavefunction
Thurs. Dec. 3, 2009
2
Phy208 Lect. 26
20
Probability of finding electron


Classically, equally likely to find particle anywhere
QM - true on average for high n
Zeroes in the probability!
Purely quantum, interference effect
Thurs. Dec. 3, 2009
Phy208 Lect. 26
21
Quantum Corral
D. Eigler (IBM)


48 Iron atoms assembled into a circular ring.
The ripples inside the ring reflect the electron quantum states of a
circular ring (interference effects).
Thurs. Dec. 3, 2009
Phy208 Lect. 26
22
Particle in box again: 2 dimensions
Motion in x direction
Motion in y direction
Same velocity (energy),
but details of motion are different.
Thurs. Dec. 3, 2009
Phy208 Lect. 26
23
Quantum Wave Functions
Probability
(2D)
Wavefunction
Ground state: same wavelength
(longest) in both x and y
Need two quantum #’s,
one for x-motion
one for y-motion
Use a pair (nx, ny)
Ground state: (1,1)
Probability = (Wavefunction)2
One-dimensional (1D) case
Thurs. Dec. 3, 2009
Phy208 Lect. 26
24
2D excited states
(nx, ny) = (2,1)
(nx, ny) = (1,2)
These have exactly the same energy, but the
probabilities look different.
The different states correspond to ball bouncing
in x or in y direction.
Thurs. Dec. 3, 2009
Phy208 Lect. 26
25
Particle in a box
What quantum state could this be?
A. nx=2, ny=2
B. nx=3, ny=2
C. nx=1, ny=2
Thurs. Dec. 3, 2009
Phy208 Lect. 26
26
Next higher energy state


Ball has same bouncing motion in x and in y.
Is higher energy than state with motion
only in x or only in y.
(nx, ny) = (2,2)
Thurs. Dec. 3, 2009
Phy208 Lect. 26
27
Three dimensions

Object can have different velocity (hence
wavelength) in x, y, or z directions.





Need three quantum numbers to label state
(nx, ny , nz) labels each quantum state
(a triplet of integers)
Each point in three-dimensional space has a
probability associated with it.
Not enough dimensions to plot probability
But can plot a surface of constant probability.
Thurs. Dec. 3, 2009
Phy208 Lect. 26
28
Particle in 3D box


Ground state
surface of constant
probability
(nx, ny, nz)=(1,1,1)
2D case
Thurs. Dec. 3, 2009
Phy208 Lect. 26
29
(121)
(112)
(211)
All these states have the same
energy, but different probabilities
Thurs. Dec. 3, 2009
Phy208 Lect. 26
30
(222)
(221)
Thurs. Dec. 3, 2009
Phy208 Lect. 26
31
3-D particle in box: summary

Three quantum numbers (nx,ny,nz) label each state

nx,y,z=1, 2, 3 … (integers starting at 1)

Each state has different motion in x, y, z

Quantum numbers determine px 

h
n
 nx
x
h
2L

Momentum in each direction: e.g.

2
2
p
p
p
Energy: E 
 y  z  E o nx2  ny2  nz2 
2m 2m 2m
2
x
Some quantum states have same energy

Thurs. Dec. 3, 2009
Phy208 Lect. 26
32