Download LHC Physics - UCL HEP Group

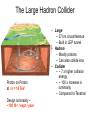
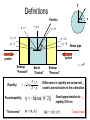
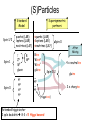
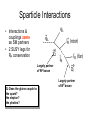
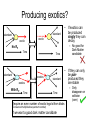
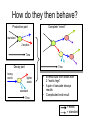
LHC Physics
Alan Barr
UCL
This morning’s stuff…
Higgs – why we expect it, how to look for it, …
Supersymmetry – similar questions!
Smorgasbord of other LHC physics
Physics at TeV-scale
• Dominated by the physics of
Electroweak Symmetry Breaking
• Answering the question:
– “Why do the W and Z bosons have mass?”
• Standard Model suggests: Higgs
mechanism
– However Higgs boson predicted by SM not
yet observed
Higgs mechanism - history
• 1964 Demonstration that a scalar field with
appropriate interactions can give mass to gauge
bosons
– Peter Higgs (Edinburgh, previously UCL)
– Independently discovered by Francois Englert and
Robert Brout (Brussels)
• Not until 1979 that Salam, Weinberg and
Glashow use this in a theory of electroweak
symmetry breaking
– For a biographic article on P. Higgs see
http://physicsweb.org/articles/world/17/7/6
Higgs mechanism: why needed?
• Example of P. Higgs – give mass to a U(1)
boson (heavy “photon” in a QED-like theory)
Start with QED Lagrangian:
where
Which is invariant under the local U(1) gauge transformation
(*)
Adding a gauge boson mass term could be attempted with a term like:
But this isn’t invariant under gauge transformation (*) so is not allowed
Instead add a complex scalar field which couples to the gauge boson
Pictorial representation
Quartic term
 selfcoupling
positive
Excitations in this direction
produce physical Higgs
boson
Excitations in this
direction = gauge
transformation
- Global transformations
unobserved
- Local transformations
give mass to gauge
bosons
Quadratic
Degenerate minimum
coupling term
Vacuum (field strength≠0)
negative
If you don’t understand this,
Scalar field strength = 0
study Phys.Lett.12:132-133,1964
Higgs field “eats Goldstone boson”
• Flat direction in potential usually
represents zero-mass particle
φ
– “Goldstone boson”
φ'
• But in Higgs theory this direction is
coupled to the gauge boson
– No massless Goldstone boson
– Instead mass term generated for
gauge boson
φ
Gauge boson
Example of a Feynman
diagram showing a
contribution to the gauge
boson mass term
N.B. Our example here was for a single complex scalar and for a U(1) field.
In the Standard Model the Higgs is an electroweak SU(2) doublet field, with 4
degrees of freedom. 3 of these are ‘eaten’ by W±, Z0, mass terms leaving a
single scalar for the physical Higgs boson.
For full SU(2) treatment see e.g. Halzen & Martin section 14.9
Constraints on the Higgs mass
•
Higgs boson mass is the remaining
unpredicted parameter in Standard Model:
•
•
•
Higgs self-couplings not predicted
So Higgs mass not predicted by Electroweak theory
However there are:
1.
Bounds from theory:
•
2.
Perterbative unitarity of boson-boson scattering
Indirect bounds
•
3.
Loop effects on gauge boson masses
Direct bounds
•
Searches
Perturbative limit
Vector Boson
scattering
Without other new physics the Higgs
boson must exist & have mass < 1 TeV
Phys.Rev.D16:1519,1977
Halzen & Martin section 15.6
Indirect Higgs bounds:
LEP Electroweak data
Measurements
• W (and Z) mass depends on
mHiggs
– Logarithmic loop corrections to
masses
– Also depends on top mass
Prediction as
a function of mH
http://lepewwg.web.cern.ch/LEPEWWG/
Direct bounds:
Higgs searches @ LEP
Higgsstrahlung – dominant production
• No discovery
• Direct lower bound at 114.4 GeV
Phys.Lett. B565 (2003) 61-75
ALEPH:
Candidate vertex:
Higgs-Hunter Situation Report
• Something very much like the Higgs must exist with:
~100 GeV < m < ~1 TeV
• No discovery as yet
• If it is a Standard Model Higgs the constraints are
tighter:
114.4 GeV < mSM Higgs < 199 GeV
The Large Hadron Collider
Proton on Proton
at √s = 14 TeV
Design luminsoity ~
~100 fb-1 / expt / year
• Large
– 27 km circumference
– Built in LEP tunnel
• Hadron
– Mostly protons
– Can also collide ions
• Collider
– ~ 7 x higher collision
energy
– ~ 100 x increase in
luminosity
– Compared to Tevatron
General Purpose Detectors
Similarities:
1. Tracker
2. Calorimeter
3. Muon chambers
ATLAS
Differences:
Size : CMS “compact”
Magnetic-field configuration
ATLAS has muon toroids
Electromagnetic-Calorimeter:
CMS crystals. ATLAS Liquid Argon
Outer tracker technology
CMS all-silicon. ATLAS straw tubes
y
Definitions
φ
Particle
η = -1
η=0
η = +1
η = -2
η = -3
x
η = +2
η = +3
θ
Beam pipe
proton
proton
Endcap
“Forward”
Rapidity:
Pseudorapidity:
“Transverse”
y  12 log
z
Barrel
“Central”
E  pz
E  pz
Endcap
“Forward”
Differences in rapidity are conserved
under Lorentz boosts in the z-direction*
   ln[tan(  / 2)]
pT = (px, py)
Good approximation to
rapidity if E>>m
|pT| = √(px2, py2)
*
*prove these!
Making particles in hadron colliders
proton
proton
• Hadron-Hadron collisions complicated
– See lectures by Mark Lancaster
(“Hadron Collider Physics”)
– QCD  Lots of background events with jets
– QCD  Lots of hadronic “rubbish” in signal events
– Hard scatters are largely from q-qbar or glue-glue
• Proton structure is important – See lectures by Robert
Thorne
• But they provide the highest energies available
• Often these are the discovery machines
LHCb
• Asymmetric detector for B-meson physics
For more information see Lazzeroni talk at:
http://indico.cern.ch/conferenceDisplay.py?confId=5426
LHCb Physics
Quark flavour e-states are not the same as mass e-states: mixing:
• VCKM must be unitary: V.V† = V †.V = 1
• Multiply out rows & columns:
Do this!
LHCb Physics
• Measurements of decay rates and kinematics tell us
about squark mixings
• Over-constraining triangles gives sensitivity to new
physics through loop effects
ALICE
• Designed to examine
collisions of heavy ions
(e.g. lead-lead or goldgold)
• Theorised to produce a
new state of matter – a
quark-gluon plasma
• Quarks no longer
confined inside
colourless baryons
• Signals for QGP:
– Jet quenching
QGP
Jet
No Jet
– Quarkonim (e.g. J/ψ)
suppression
(“melt bound states”)
c
J/ψ
_
c
Couplings of the SM Higgs
• Couplings
proportional
to mass
• What does
this mean for
the Higgshunter?
Producing a Higgs
• Higgs couplings
 mass
– u-ubar  H
has very small
cross-section
– Dominant
production via
vertices coupling
Higgs to heavy
quarks or W/Z
bosons
Production cross-sections
Decay of the SM Higgs
• Width becomes large as WW mode opens
• Branching ratios change rapidly as new
channels become kinematically accessible
Needle in a haystack…
QCD jet production
at high energy
Higgs production
Need to use signatures
with small backgrounds:
- Leptons
- High-mass resonances
- Heavy quarks
to avoid being overwhelmed
Example 1 : H  ZZ
• Only works when mHiggs >~ 2.MZ
• When the Z decays to leptons there are
small backgrounds
e+
q
_
q
Z
e-
Z
e+
H
e-
H  ZZ
CMS
H  ZZ  e+e- e+eElectrons have track (green ) & energy deposit (pink)
H  ZZ  e+e- e+ee+
q
_
q
e-
Z
mH=150
background
H
e+
Z
mH=130
mH=170
e-
1. Find events consistent
with above topology
(four electrons)
2. Add together the four
electron 4-vectors
3. Find the mass of the resultant
4-vector ( mass of the Higgs)
Plot shows simulated
distributions of [invariant
mass of four electrons] for 3
different values of mHiggs
(We wouldn’t see all of these together!)
Example (2): H  γγ
• No direct coupling
of H to photon
• However allowed at
loop level
• Branching ratio:
~ 10 -3
(at low mHiggs)
• Important at low
mass
• Actually a very
clean way of
looking for Higgs
– Small backgrounds
Production and decay of Higgs
through ‘forbidden’ direct couplings
γ
γ
H γγ CMS simulation. Physics TDR, 2006
H  γγ
Higgs signal
scaled up by
factor 10!
Invariant mass of the pair of photons
• Simulation by CMS for different Higgs masses
for early LHC data (1 fb-1)
H  γγ … backgrounds
“Irreducible”
2 real photons
“Born”
“Box”
“Reducible”
e.g. fake photons
γ
q
_
q
gluon
π0
γ
γ
Need v. good
calorimeter
segmentation
to separate these
Significance
H->ZZ
Significance is a measure
of the answer to the question
“What is the probability
that a background
fluctuation would produce
what I am seeing”
5- means “probability
that background
fluctuation does this is
less than 2.85·10-7 ”
5- is usually taken
as benchmark
for “discovery”
After discovery of Higgs?
• Measure Higgs mass
– The remaining unconstrained parameter of the Standard Model
• Measure Higgs couplings to fermions and vector
bosons
– All predicted by Standard Model
– Check Higgs mechanism
• Couplings very important since there may be more than
one Higgs boson
– Theories beyond the Standard Model (such as Supersymmetry)
predict multiple Higgs bosons.
– In such models the couplings would be modified
• Do direct searches for further Higgs bosons!
If no Higgs found?
• Arguably more exciting than finding Higgs
• Look at WW scattering process
– Look for whatever is “fixing” the cross-section
– E.g. exotic resonances
What is supersymmetry?
• Nature permits only
particular types of
symmetry:
– Space & time
• Lorentz transforms
• Rotations and translations
– Gauge symmetry
• Such as Standard Model
force symmetries
• SU(3)c x SU(2)L x U(1)
– Supersymmetry
• Anti-commuting
(Fermionic) generators
• Changes Fermions into
Bosons and vice-versa
Examples of Supersymmetric partner-states
• Consequences?
– Supersymmetric theory has
a Boson for every Fermion
and vice-versa
• Doubles the particle
content
– Partners to Standard Model
particles not yet observed
(S)Particles
Standard
Model
Spin-1/2
Spin-1
Spin-0
quarks (L&R)
leptons (L&R)
neutrinos (L&?)

Z0
W±
gluon
h0
H0
A0
H±
B
W0
Supersymmetric
partners
squarks (L&R)
sleptons (L&R)
sneutrinos (L&?)
Bino
Wino0
Wino±
gluino
Spin-0
After
Mixing
4 x neutralino
Spin-1/2
~
H0
~
H±
gluino
2 x chargino
(Higgsinos)
Extended higgs sector
2 cplx doublets  8-3 = 5 Higgs bosons!
Why Supersymmetry?
• Higgs mass
– Quantum corrections to mH
– Would make “natural” mass near
cut-off (Unification or Planck
scale)
– But we know mH <~ 1 TeV
– mH = mH bare + DmH
– Severe fine tuning required
between two very big numbers
• Enter Supersymmetry (SUSY)
– Scalar partner of quarks also
provide quantum corrections
– Factor of -1 from Feynman rules
– Same coupling, λ
– Quadratic corrections cancel
– mH now natrually at electroweak
scale
top
λ
higgs
λ
higgs
Δm2(h)  Λ2cutoff
Quantum correction to mHiggs
λ
higgs
stop
λ
higgs
Cancelling correction to mHiggs
Further advantages
• Lightest SUSY
particle is:
–
–
–
–
Big Bang relic abundance
calculations are in good
agreement with WMAP
microwave background
observations in regions of
SUSY parameter space
Light
Weakly interacting
Stable
Massive
• Good dark matter
candidate
1/α
• Predicts gauge
unification
– Extra particles modify
running of couplings
– Step towards “higher
things”
miss
1/α
+SUSY
Hit!
SM
Log10 (μ / GeV)
Log10 (μ / GeV)
R-parity
• Multiplicative discrete
quantum number
• RP = (-1)2s+3B+L
– S=spin, B=baryon number,
L=lepton number
• Standard Model particles have
RP = +1
• SUSY Model particles have
RP = -1
• If RP is conserved then SUSY
particles must be pairproduced
• If RP is conserved then the
Lightest Supersymmetric
Particle (LSP) is stable
Example of a Feynman
diagram for proton decay
which is allowed if the RPviolating couplings (λ) are
not zero
How is SUSY broken?
Weak
coupling
(mediation)
• Direct breaking in
visible sector not
possible
– Would require
squarks/sleptons with
mass < mSM
– Not observed!
• Must be strongly
broken “elsewhere”
and then mediated
– Soft breaking terms
enter in visible sector
– (>100 parameters)
Soft SUSYbreaking terms
enter lagrangian
in visible sector
Strongly
broken
sector
Various models offer different
mediation e.g.
Gauge  “GMSB”
Gravity  “mSUGRA”
(supergravity)
Anomaly  “AMSB”
Sparticle Interactions
• Interactions &
couplings same
as SM partners
• 2 SUSY legs for
RP conservation
Largely partner
of W0 boson
Q: Does the gluino couple to:
the quark?
the slepton?
the photino?
Largely partner
of W0 boson
General features
Mass/GeV
Production dominated
by squarks and gluinos
• Complicated
cascade decays
– Many
intermediates
• Typical signal
– Jets
• Squarks and
Gluinos
– Leptons
• Sleptons and weak
gauginos
– Missing energy
“typical” susy spectrum
(mSUGRA)
• Undetected
Lightest Susy
Particle
The “real thing”
(a simulation of…)
• Two high-energy
jets of particles
Invisible
particles
– Visible decay
products
• “Missing”
momentum
– From two
invisible
particles
– these are the
invisible Dark
Matter guys
Proton beams perpendicular to screen
Standard Model backgrounds:
measure from LHC DATA
mμ
μ
m
n
n
With SUSY
Measure in
Z -> μμ
Use in
Z -> νν
R: Z > nn
B: Estimated
• Example: background
to “4 jets + missing energy”
– Measure background in control region
– Extrapolate to signal region
– Look for excess in signal region
Missing PT / GeV
Constraining SUSY masses
• Mass constraints
• Invariant masses in pairs
– Missing energy
– Kinematic edges
Observable:
Frequentlystudied
decay chain
Depends on:
Limits depend on
angles between
sparticle decays
Mass determination
Measure
edges
Try various
masses in
equations
C.G. Lester
Variety of edges/variables
• Narrow bands in ΔM
• Wider in mass scale
• Improve using crosssection information
These measurements can tell us about SUSY breaking
Other things to do with SUSY
• Measure the sparticle spins
– “prove” that it is really supersymmetric
partners we are seeing
• Measuring the couplings & mixings
– Use to “predict” Dark Matter relic density
• Find the extra Higgs bosons
– Recall that SUSY predicts 5 Higgs bosons
– Now we want to find H0, h0, A0, H±
– Also measure their couplings, CP, …
Standard Model Physics
• The ATLAS and CMS
experiments also potentially can
measure:
–
–
–
–
Top mass
W mass
Rare B-meson decay rates
Jet physics
• To much higher precision that is
currently achievable
– Large number of e.g. top quarks
produced
– Small statistical errors
– Systematic errors (such as jet
energy scale determination) limiting
Mass of hadronic top
Other things to look for…
• Leptoquarks
– Motivated by Grand Unified Theories
– Carry lepton and baryon number
– E.g. LQ  bμ
• New heavy quarks
– Predicted by some non-SM Higgs theories
• New heavy gauge bosons
– Indications of new symmetry groups
• Extra dimensions
– Large variety of models on the market!
Extra dimensions models
• Motivated by need for ED in string theory and
m-theory
– Logical a possibility for a LHC discovery
• Different models…
– Which particles are localised where (bulk/brane)
– Form of space-time metric (flat/warped)
– Geometry and size of extra dimensions
• …make different predictions
–
–
–
–
–
Kalazua-Klein resonances of SM particles
Graviton states
Stringy resonances
Effects of strong gravity (micro Black Holes)
Energy loss into extra dimensions
More information:
http://eps2003.physik.rwth-aachen.de/data/talks/parallel/09StringTheory/09Vacavant.ppt
General sources
• Higgs at the LHC: talk by Zeppenfeld
http://whepp9.iopb.res.in/talks/zeppenfeld_WHEPP9.pdf
• Physics at the LHC: Higgs talk by Harlander:
http://newton.ftj.agh.edu.pl/physLHC/
• ATLAS physics Technical Design Report (TDR)
http://atlas.web.cern.ch/Atlas/GROUPS/PHYSICS/TDR/a
ccess.html (1999)
• CMS physics Technical Design Report (TDR)
http://cmsdoc.cern.ch/cms/cpt/tdr/ (2006)
• Supersymmetry: http://arxiv.org/abs/hep-ph/9709356
Constraints on mHiggs
No perturbative unitarity
Unstable vacuum
Scale at which new physics enters
Producing a Higgs @ LHC
q
g
g
H
_
q
W/Z
g
H
H
top
g
top
• Higgs couplings  mass
– Direct e.g. u-ubar  H
very small cross-section
• Dominant production via
vertices coupling Higgs to
heavy quarks or W/Z
bosons
q
_
q
H
W/Z
Higgs’ mechanism
• Add a complex scalar field
– In fact he adds 2 real scalar fields,
(fermion part of L now ignored)
This is gauge invariant when the scalars have covariant derivatives:
Now if the potential, V, has a degenerate
minimum at φ≠0 we get interesting
consequences…
N.B. scalar field
must couple to
gauge field like
this for the Higgs
mechanism to work
mSUGRA – “super gravity”
• A.K.A. cMSSM
• Gravity mediated SUSY
breaking
1016 GeV Unification of couplings
– Flavour-blind (no FCNCs)
Iterate using
Renormalisation
Group
Equations
• Strong expt. limits
– Unification at high scales
• Reduce SUSY parameter
space
– Common scalar mass M0
• squarks, sleptons
– Common fermionic mass M½
• Gauginos
– Common trilinear couplings A0
• Susy equivalent of Yukawas
EW scale
Correct MZ, MW, …
Programs include
e.g. ISASUSY,
SOFTSUSY
Other suggestions for SUSY
breaking
• Gauge mediation
– Gauge (SM) fields in extra dimensions mediate SUSY breaking
• Automatic diagonal couplings  no EWSB
– No direct gravitino mass until Mpl
• Lightest SUSY particle is gravitino
• Next-to-lightest can be long-lived (e.g. stau or neutralino)
• Anomaly mediation
– Sequestered sector (via extra dimension)
• Loop diagram in scalar part of graviton mediates SUSY breaking
• Dominates in absence of direct couplings
– Leads to SUSY breaking  RGE β-functions
• Neutral Wino LSP
• Charged Wino near-degenerate with LSP  lifetime
• Interesting track signatures
Not exhaustive!
Producing exotics?
standard
standard
exotic
exotic
No RP
Time
standard
Time
exotics
standard
exotics
With RP
Time
Time
Require an even number of exotic legs to/from blobs
(Conserved multiplicative quantum number)
If we want a good dark matter candidate
• If exotics can
be produced
singly they can
decay
– No good for
Dark Matter
candidate
• If they can only
be pairproduced they
are stable
– Only
disappear on
collision
(rare)
How do they then behave?
Complete “event”
Production part
standard
2 exotics
Time
Decay part
heavy
exotic
Time
lighter
exotic
standard
Time
•
•
•
Events build from blobs with
2 “exotic legs”
A pair of cascade decays
results
Complicated end result
= exotic
= standard