* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Chapter 9 Population genetics part IIIa Linkage
Artificial gene synthesis wikipedia , lookup
History of genetic engineering wikipedia , lookup
Pharmacogenomics wikipedia , lookup
Heritability of IQ wikipedia , lookup
Behavioural genetics wikipedia , lookup
Gene expression programming wikipedia , lookup
Epigenetics of human development wikipedia , lookup
Skewed X-inactivation wikipedia , lookup
Genomic imprinting wikipedia , lookup
X-inactivation wikipedia , lookup
Medical genetics wikipedia , lookup
Site-specific recombinase technology wikipedia , lookup
Designer baby wikipedia , lookup
Genome (book) wikipedia , lookup
Human genetic variation wikipedia , lookup
Genome-wide association study wikipedia , lookup
Polymorphism (biology) wikipedia , lookup
Human leukocyte antigen wikipedia , lookup
Quantitative trait locus wikipedia , lookup
HLA A1-B8-DR3-DQ2 wikipedia , lookup
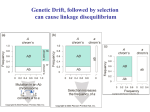
Genetic drift wikipedia , lookup
Dominance (genetics) wikipedia , lookup
Hardy–Weinberg principle wikipedia , lookup
Microevolution wikipedia , lookup
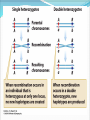
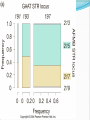
Chapter 9 Quantitative Genetics Read Chapter 9. Traits such as cystic fibrosis or flower color in peas produce distinct phenotypes that are readily distinguished. Such discrete traits, which are determined by a single gene, are the minority in nature. Most traits are determined by the effects of multiple genes. Continuous variation However, traits determined by many genes (polygenic traits) show continuous variation. Grain color in winter wheat is determined by three alleles at three loci. Additive effects of genes The genes affecting color of winter wheat interact in a particularly straightforward way. They have additive genetic effects. This means that the phenotype for an individual is obtained just by summing the effects of individual alleles. The more alleles for dark color an individual has the darker it will be Continuous variation Examples in humans of traits that show continuous variation include height, intelligence, athletic ability, and skin color. Quantitative traits For continuous traits we cannot assign individuals to discrete categories. Instead we must measure them. Therefore, characters with continuously distributed phenotypes are called quantitative traits. Quantitative traits Quantitative traits determined by influence of (1) genes and (2) environment. East (1916) In early 20th century there was considerable debate over whether Mendelian genetics could explain continuous traits. Edward East (1916) showed it could. Studied longflower tobacco (Nicotiana longiflora) East (1916) East studied corolla length (part of flower) in tobacco flowers. Crossed pure breeding short and long corolla individuals to produce F1 generation. Crossed F1’s to create F2 generation. East (1916) Using Mendelian genetics we can predict expected character distributions if character determined by one gene, two genes, or more etc. East (1916) Depending on number of genes: models predict different numbers of phenotypes. One gene: 3 phenotypes Two genes: 5 phenotypes Six genes: 13 phenotypes. Continuous distribution. East (1916) How do we decide if a quantitative trait is under the control of many genes? In one and two locus models many F2 plants have phenotypes like the parental strains. Not so with 6-locus model. Just 1 in 4,096 individuals will have the genotype aabbccddeeff. East (1916) But, if Mendelian model works you should be able to recover the parental phenotypes through selective breeding. East selectively bred for both short and long corollas. By generation 5 most plants had corolla lengths within the range of the original parents. East (1916) Plants in F5 generation of course were not exactly the same size as their ancestors even though they were genetically identical. Why? East (1916) Environmental effects. Depending on environment genetically identical organisms may differ greatly in phenotype. Genetically identical plants grown at different elevations differ enormously (Clausen et al. 1948) The importance of latent variation Early work in the 2oth century on polygenic traits showed that new types or values of traits not seen in a parent population could appear in offspring produced by that population. It was unclear where these new variants came from. It’s easy to see in figure A (next slide) how natural selection could favor some members of a population so that after a time the mean values of a population would increase within the range of previous variation. The importance of latent variation However, it’s less clear how a population could as a result of natural selection arrive at B in the previous slide in which the selected population is outside the range of the original population. The key to understanding this phenomenon is to realize that when multiple genes contribute to a trait there will be many, many unique combinations of alleles that produce different phenotypes. A population is not likely to include all of these possibilities. Thus, a new variant can contain an assortment of alleles not seen previously. See next slide. Gene interactions Not all genes interact additively with the alleles’ effects summing together. In many cases genes interact with each other nonadditively a phenomenon we call epistasis. Gene interactions For example, two loci influence coat color in oldfield mice, but they interact epistatically. The effect of the Mc1R allele depends on which alleles are present at the agouti locus (next slide). Population genetics of multiple loci A locus is the physical location on a chromosome where a gene occurs. Different versions of a gene are called alelles. The Hardy-Weinberg models we have discussed so far are quite simple because they consider only a single locus and its alleles. However, many traits are controlled by the combined influence of many genes. Population genetics of multiple loci Genes located on different chromosomes segregate (i.e. they enter gametes) independently of each other. However, when genes are located on the same chromosome they frequently do not segregate independently, especially if they are located close to each other on a chromosome. Such loci have a physical linkage. Population genetics of multiple loci The closer together two loci are on a chromosome the less likely it is that crossing over will occur between the loci during meiosis and split them up. In most cases they will be inherited as a pair. Population genetics of multiple loci Consider a pair of loci located on same chromosome. Gene at locus A has two alleles A and a Gene at locus B has two alleles B and b Population genetics of multiple loci In two-locus Hardy-Weinberg analysis we track allele and chromosome frequencies. Thus 4 possible chromosome genotypes are possible in previous slide: AB, Ab, aB, ab A multilocus genotype is referred to as a haplotype (from haploid genotype). Statistical associations between loci Does selection on locus A affect our ability to make predictions about evolution at locus B? Sometimes. Depends on whether loci are in linkage equilibrium or linkage disequilibrium. Statistical associations between loci Two loci in a population are in linkage equilibrium when the genotype of a chromosome at one locus is independent of the genotype at the other locus on the same chromosome. I.e. knowing genotype at one locus is of no use in predicting genotype at the other locus. Statistical associations between loci In contrast two loci are said to be in linkage disequilibrium when knowing the allele at one locus enables you to predict what the allele at the other locus likely is. For example in a population where there are AB, Ab, and aB haplotypes, but no ab haplotypes if we know an individual has a b allele we know that individual also has at least one A allele. Quantifying linkage disequilibrium To measure the associations between allele frequencies at two loci A and B we examine the haplotype frequencies at these loci. Let fA, fB, fa and f b be the frequencies of the A, B, a and b alleles respectively. Let hAB, hAb, haB, hab be the haplotype frequencies of AB, Ab, aB and ab haplotypes. Quantifying linkage disequilibrium If the allele at the A locus occurs independently of the allele at the B locus then the haplotype frequencies will be: hAB = fAfB hAb = fAf b haB = fafB hab = faf b Quantifying linkage disequilibrium So the expected haplotype frequency is found just by multiplying the appropriate allele frequencies by each other. If the frequency of allele A (fA) = 0.7 and the frequency of allele B (fB) = 0.8 then the expected haplotype frequency hAB, if the alleles are in linkage equilibrium, would be 0.56. Coefficient of linkage disequilibrium To measure the degree of linkage disequilibrium we can calculate a coefficient of linkage disequilibroum (D). For a given haplotype this is defined as the difference between the actual frequency we observe of a haplotype, e.g. AB, and the expected frequency fAfB of the same haplotype if the loci are independent. D = hAB - fAfB Coefficient of linkage disequilibrium When the alleles at each locus occur independently then the coefficient of linkage disequilibrium will be zero. We then say the alleles are in linkage equilibrium. If the alleles at each locus occur non-independently then the value of D will be non-zero and we say they are in linkage disequilibrium. Coefficient of linkage disequilibrium In a gene pool the frequencies of the alleles are as follows: A = 0.4, a= 0.6, B=0.3 and b= 0.7. The haplotype frequencies are AB = 0.12, Ab =0.28, aB = 0.18 and ab=0.42. Is the population in linkage equilibrium? Coefficient of linkage disequilibrium Yes. hAB = 0.12 hAb = 0.28 haB = 0.18 hab = 0.42 fAfB = 0.3*0.4 = 0.12 fAf b = 0.4*0.7 = 0.28 fafB = 0.6*0.3 = 0.18 faf b = 0.6*0.7 = 0.42 For each haplotype D = zero e.g. D = hAB – fAfB = 0.12-0.12 = 0 Coefficient of linkage disequilibrium In a second gene pool the frequencies of the alleles are as follows: A = 0.6, a= 0.4, B=0.8 and b= 0.2 The observed haplotype frequencies are AB = 0.44, Ab =0.16, aB = 0.36 and ab=0.04. Is this population in linkage equilibrium? Coefficient of linkage disequilibrium No. hAB = 0.44 hAb = 0.16 haB = 0.36 hab = 0.04 fAfB = 0.6*0.8 = 0.48 fAf b = 0.6*0.2 = 0.12 fafB = 0.4*0.8 = 0.32 faf b = 0.4*0.2 = 0.08 For each haplotype D not equal to zero e.g. D = hAB – fAfB = 0.44-0.48 = -0.04 Coefficient of linkage disequilibrium Another way to calculate the coefficient of linkage equilibrium if we just know haplotype frequencies is the following equation: D = hABhab - hAbhaB The value of this equation will be zero if the haplotypes are in linkage equilibrium. Proof of the formula for linkage disequilibrium D = hABhab - hAbhaB Let p and q be the frequencies of alleles A and a. Let s and t be the frequencies of alleles B and b. If the population is in linkage equilibrium then hAB = ps, hab = qt, hAb = pt, haB = qs Therefore rewriting the equation for linkage disequilibrium in terms of allele frequencies we get D = psqt - ptqs which equals zero if the population is in linkage equilibrium. Any value of D not equal to zero implies the population is in linkage disequilibrium. Coefficient of linkage disequilibrium Is this population, which has the following haplotypes, in linkage equilibrium? AB= 0.46, Ab = 0.14 aB = 0.34 ab= 0.06 Coefficient of linkage disequilibrium Use the formula: D = hABhab - hAbhaB D = 0.46*0.06 – 0.14*0.34 D = 0.0276 – 0.0476 = -0.02 D is not equal to zero, so the population is in linkage disequilibrium. Coefficient of linkage disequilibrium The maximum value for D is 0.25 when AB and ab are the only haplotypes present and each has a frequency of 0.5. The minimum value for D is -0.25 when Ab and aB are the only haplotypes present and each has a frequency of 0.5. This formula thus tells us not only whether a population is in linkage disequilibrium but how strong the disequilibrium is. What creates linkage disequilibrium in populations? Multiple Mechanisms: Mutation Selection on multilocus genotypes. Genetic drift Migration Mutation A population contains only the haplotypes AB and aB. A mutation occurs with the haplotype aB so that B mutates to b producing the haplotype ab. This population will have the genotype aB , AB and ab, but there will be no Ab haplotypes. Hence, the population will be in linkage disequilibrium because of the missing Ab haplotype. Selection on multilocus genotypes. Scenario: Either of two biosynthetic pathways is sufficient to produce an essential molecule from two precursor molecules. Each pathway is controlled by a single locus. The functional wild-type alleles (A & B) are dominant over the nonfunctional recessive alleles (a & b). Only aabb individuals cannot produce the essential molecule. Selection on multilocus genotypes. Because of selection against the aabb genotype there will be fewer ab haplotypes than we would expect based on the allele frequencies of a and b. Genetic drift Scenario: Small population with two genotypes AB and Ab. No copies of allele a. Single Ab chromosome mutation converts an A to an a. This single ab chromosome puts population in linkage disequilibrium. Scenario is drift because only in a small population would you expect to have only a single mutation of A to a. In large population you would expect many mutations of A to a and a to A. Genetic drift Scenario: a small population with AB, Ab, aB and ab haplotypes where there is a low recombination rate between the A and B loci. Drift can lead to the loss of alleles in a small population and haplotypes can disappear even more easily. If by chance all of one haplotype disappears then the population will have only three haplotypes. Haplotypes need not necessarily disappear. In a small population random fluctuations in haplotype frequencies can easily lead to statistical associations between alleles and create linkage disequilibrium. Migration Scenario: Suppose that the a & b alleles are fixed in a mainland lizard population and the A&B alleles in an island lizard population. Mainland thus has only the ab haplotype and the island the AB haplotype. If some individuals migrate from the mainland to the island ab haplotypes will be introduced. The population will be in linkage disequilibrium initially because there will be no aB and Ab haplotypes and a strong statistical association between the A and B alleles. What eliminates linkage disequilibrium from a population? A population in linkage disequilibrium will not stay in that state forever. Unless no other evolutionary process prevents it (e.g. selection) linkage is broken down by recombination. What eliminates linkage disequilibrium from a population? Sexual reproduction steadily reduces linkage disequilibrium. Crossing over during meiosis breaks up old combinations of alleles and creates new combinations. Genetic recombination Genetic recombination tends to randomize genotypes in relation to other genotypes (i.e., it reduces linkage disequilibrium.) Rate of decline in linkage disequilibrium is proportional to rate of recombination. r is recombination rate, r is related to how far apart two loci are on a chromosome. Empirical example of genetic recombination Clegg et al. (1980) established two fruit fly populations that were in linkage disequilibrium. Population 1 AB and ab each 0.5 frequency. Population 2 aB and Ab each 0.5 frequency. Empirical example of genetic recombination Populations of about 1,000 individuals maintained for 48-50 generations. Flies allowed to mate freely. Populations sampled every 1-2 generations to count frequencies of 4 haplotypes. Empirical example of genetic recombination Crossing-over created missing haplotypes in each population and linkage disequilibrium disappeared. In general, in random-mating populations sex is efficient enough at eliminating linkage disequilibrium that most alleles are in linkage equilibrium most of the time. Practical reasons to measure linkage disequilibrium There are two major uses of measures of linkage disequilibrium. Can be used to reconstruct history of genes and populations Can be used to identify alleles recently favored by positive selection Reconstructing history of the CCR5-Δ32 locus HIV is the virus responsible for AIDS. It parasitizes macrophages and T-cells of immune system. It enters by binding to two protein receptors on cell’s surface : CD4 and a coreceptor, usually CCR5. Some people appear resistant to the virus even though exposed multiple times. Some resistant individuals possess a mutant CCR5 coreceptor protein whose gene is missing 32 base pairs. This allele is referred to as the CCR5 Δ32 allele. Reconstructing history of the CCR5-Δ32 locus Frequency of the CCR5-Δ32 allele is highest in European populations (9%), but scarce or absent elsewhere. Where did the CCR5-Δ32 allele come from and when did it originate? Reconstructing history of the CCR5-Δ32 locus CCR5-Δ32 is located on chromosome 3 and near two short-tandem repeat sites called GAAT and AFMB. GAAT and AFMB are non-coding and have no effect on fitness. Both GAAT and AFMB have a number of different alleles. Reconstructing history of the CCR5-Δ32 locus Stephens et al. (1998) examined haplotypes of 192 Europeans. Found that GAAT and AFMB alleles were in close to linkage equilibrium with each other. Reconstructing history of the CCR5-Δ32 locus However, CCR5 is in strong linkage disequilibrium with both GAAT and AFMB. Almost all chromosomes carrying CCR5-Δ32 also carry allele 197 at GAAT and allele 215 at AFMB. Reconstructing history of the CCR5-Δ32 locus Most likely reason for observed linkage disequilibrium is genetic drift. Hypothesis: in past was originally only one CCR5 allele the CCR5+ allele. Then a mutation on a chromosome with the haplotype CCR5--GAAT-197--AFMB-215 created the CCR5Δ32 allele. Reconstructing history of the CCR5-Δ32 locus The CCR5Δ32 allele was favored by selection and rose to high frequency dragging the other two alleles with it. Since its appearance and spread, crossing over and mutation have been breaking down the linkage disequilibrium. Now about 15% of Δ32-197-215 haplotypes have changed to other haplotypes. Reconstructing history of the CCR5-Δ32 locus Based on rates of crossing over and mutation rates, Stephens et al. (1998) estimate the CCR5-Δ32 allele first appeared about 700 years ago (range of estimates 275-1875 years) Reconstructing history of the CCR5-Δ32 locus Because the CCR5-Δ32 increased in frequency so rapidly selection must have been strong. Most obvious candidate is an epidemic disease. Myxoma virus a relative of smallpox uses CCR5 protein on cell surface to enter host cell, which suggests the epidemic disease that favored CCR5-Δ32 may have been smallpox. However, timing of origin also closely matches period of bubonic plague. Using linkage disequilibrium to detect strong positive selection. A new mutant allele will be in linkage disequilibrium when it first appears. If it persists, it may increase in frequency. Over time linkage disequilibrium will break down as a result of recombination from crossing over. Linkage disequilibrium breaks down fastest for loci further apart on a chromosome because crossing over take place more often between distant loci. Using linkage disequilibrium to detect strong positive selection. High linkage disequilibrium indicates an allele originated recently. Also, expect a recently mutated allele to be rare unless selection strongly favors it. Using linkage disequilibrium to detect strong positive selection. If an allele is common, but has high linkage disequilibrium, especially with loci that are located far away on the chromosome, this suggests that the allele has been strongly selected for and must have originated recently. If the allele had arisen a long time ago, sex should have eliminated the linkage disequilibrium. Using linkage disequilibrium to detect positive selection. An allele of G6PD (Glucose-6-phosphate dehydrogenase), G6PD-202A has a high frequency (~18% in African populations) and has a high degree of linkage disequilibrium. Thus, it appears to have been strongly selected for recently. G6PD and malaria There are many common G6PD deficiencies and their distribution corresponds closely with the distribution of malaria. Appears that G6PD-202A confers strong protection against malaria.