Download Metabolic Model Describing Growth of Substrate Uptake

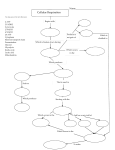
Metabolic Model Describing Growth
of Substrate Uptake
By
Idelfonso Arrieta
Anant Kumar Upadhyayula
Objectives

Explain the Growth of substrate uptake

Simulate a range of metabolic responses
obtained from Trigonopsis variabilis by
simple biochemical reactions produced in a
cell
1 of 2
Objectives

Understand the behavior of yeast under
different growth conditions

Simulate the growth of any yeast under
discontinuous conditions
1 of 2
Introduction

The yeast Trigonopsis variabilis has been reported to be a
potent producer of this enzyme.

Aerobic metabolism of all yeast is determined by relative
sizes of the sugar transport rate into the cell and the
Pyruvate transport into the mitochondrion.
Introduction

Fermentation models are normally divided into two
classes
1.
Unstructured models where the biomass is described by
one variable
Structured models where intracellular metabolic
pathways are considered.
2.
Generic Yeast cell with Main Metabolic Pathways
S
Cell
membrane
rsug
Sugar
Transport
S’
Growth
Glycolisis
ret
rrigr
RI
rrimit
Ethanol  CO2
Respiratory
Intermediate
systems
Mitochondrial
membrane
rrimit
RI’TCA
'
Cycle
CO2  H 2 O
Description of the model structure
The model describes seven major steps in yeast
metabolism:




Sugar transport across the plasma membrane.
Sugar conversion to growth macromolecules.
Glycolytic conversion of sugar to pyruvate
Pyruvate conversion to growth macromolecules.
Description of the model structure



Pyruvate conversion to ethanol product
Pyruvate transport across the mithocondrial
membrane.
Respiration of pyruvate to carbon dioxide
and water.
Assumptions





Cell matter and culture medium form a distributed system
The limiting substrate is both the carbon and energy
source.
The composition and metabolic activity assumed constant
such that biomass may be described by a single variable X.
The redox state of the cell is assumed to be the same as
that of the substrate.
ATP generation is only a result of fermentation and
respiration.
Assumptions

All growth yields (g biomass/g substrate) are constant
since YATP (g biomass/mol ATP), the PO ratio (mol
ATP/atom oxygen), and growth stoichiometry.

The carbon content of the intermediates for biosynthesis of
cell material is provided from both sugar and pyruvate.
Assumptions

Saturation of the respiratory capacity is the only
controlling factor in fermentation and respiration.

ATP is a product of energy-producing reactions and is only
a hypothetical value in this model.
Biochemical Reactions Sequence
x  S  x  S
Where :
x : Biomass Concentration (g/l)
S : Substrate Concentration (mM)
S  : Substrate Concentration inside the cell (mM)
Biochemical Reactions Sequence
x  S   x  pir .RI  pir . ATP
where,
x : Biomass concentrat ion (g/l )
S  : Substrate concentrat ion inside the cell (mM)
RI : Pyruvate concentrat ion inside the cell (mM)
ATP : Hypothetic al adenosine triphosph ate concentrat ion (mM)
pir  2
Biochemical Reactions Sequence
x  RI  x  RI 
where :
x : Biomassconcentration (g/l)
RI : Pyruvateconcentration inside thecell (mM)
RI  : Pyrovateconcentration mithocondrium (nM)
Biochemical Reactions Sequence
x  RI   x  CO 2  3 H 2 O  4 NADH  ATP
where :
NADH : hy pothetical nicotam ideadenine
dinucleotide concentration (m M)
RI  Et  CO2
Biochemical Reactions Sequence
 1 
  2x
x  a1.S   a2 .RI  
Y

 x / ATP 
where :
-1
a1 : Mass of Substrate used for the biosynthesis of biomass (mmol Sg x )
-1
a2 : Mass of pyruvate used for the biosynthesis of biomass (mmol Sg x )
-1
Yx / ATP : Biomass yield related to the ATP consumption (g x mol ATP)
Rate Equations
1. Balance to S (Glucose in the culture medium)
It is consumed through the cellular membrane





 
 dS  k .x S
dt 1 K s  S
K
1





 
1 1
Maximum Substrate Uptake rate mmol S g .h
Rate Equations
2.Balance to S’(Glucose inside the cell)
It is consumed by the transportation of S through the cellular
Membrane





 





 










k
 


1 dS '  k
a
1
a
2

S
 k
*S '   k gr *S ' .RI 

1 Ks  S
glyc.  
x dt






k gr
Kinetic constant in the Growth reactions
k
Kinetic constant of the glycolysis process
glyc.
Rate Equations
3.Balance to RI (Pyruvate)
It is generated through the Glycolysis of S’ and it is consumed
toward the interior of the mitochondrion to form the new cell
The experimental work with T. variabilis has shown a negligible
quantity of Ethanol produced in aerobic growth conditions
1  dRI 



x dt








 2. k
glyc












.S '  k








2 K
RI
rimit
 RI













a1 a2
 k gr .S ' .RI








Rate Equations
4. Balance to RI’ (pyruvate inside mithocondrion)
It is generated by the transport of RI toward the
mithocondrion.









1
dR
I

k
2 K
x dt






K
2







RI
rimit









3
 Kox.RI (O ) 
2 
 RI






Maximum pyruvate transport rate
K
rimit
Saturation constant for pyruvate transport across
the mithocondrial membrane
Kox
Oxidation constant
Rate Equations
5. Balance to x
New cells are generated in the growth reaction
a
a 
1 dx  K .S  1 RI 2 

gr

x dt







K gr












Kinetic constant in the growth reaction.
Rate Equations
6. Balance to oxygen inside the cell
It is consumed by the cells during the respiration









 



 
dO
3



1
2   K  S    K .RI O  
x dt  3 K s  S   ox  2  



K
3
Maximum specific oxygen uptake rate.
Kox
Oxidation constant.
Rate Equations
7. Balance to ATP
It is generated during the glycolysis and respiration
process.It is consumed in the generation reaction of
new cells




 
a
a 

3

 
 






1
 K
 1 RI 2 
2 K
.S    4 1 Kox.RI O    
.
S

gr



glic   P / O 
 2    Y





 

 x / ATP 
K
Kinetic constant of the glycolysis process
glyc
Kox
K gr
Oxidation constant.
Kinetic constant in the growth reaction.
Computation Procedure
Initial estimation for the parameters :
k1 : Given a value similar to the experiment al specific rate of
sugar uptake (1.5mmol S g 1 h 1 )
k 2 (mmol RI g -1h 1 ) : Value similar to k1
k3 : Given a value similar to the experiment al specific rate of
oxygen uptake (1.5mmol O2 g 1 h 1 )
COMPUTATION PROCEDURES
k glyc (( mmolRI ).1mmol 1 S g 1 h 1 ) : Value similar to k1 and k 2
k resp (14 ( mmolO2 )  2 .( mmol 1 RI g 1 h 1 )) : Value lower than k3
kimit : Given a small value such that the mithocondr ial membrane was
saturated (0.003mM )
k s ( nM ) : Given typi cal values reprted in the literature
P / O ( mol ATP mol 1 O2 ) : Given Typical values reported in the
literature
Yx / ATP ( g x mol 1 ATP) : Given typi cal values reported in the
literature
Computation procedure
The values of the parameters included in
are calculated with the following numerical
methods:
 Runge-Kutta (fourth order).
 Comparation of theoretical data and experimental data and
the best values calculated by least squares method.
Results

Since the model discussed in this paper can be used to
simulate not only an exceptional growth but also a
substrate starvation process, so it cave be sued to simulate
the growth of any yeast under
discontinuous conditions.
k
The maximum specific substrate uptake rate for the rich
medium is considerably greater to that of the salts medium.
The observed specific oxygen uptake rate k3 does not
reach a maximum for higher concentration of of oxygen
because the growth is performed under limiting conditions
of oxygen(0.5%).
3


Results

The cellular yield concerning the glucose reaches a higher value in the
rich medium compared to with the salt medium, since in using the rich
medium a large part of the carbonated chains that constitute the
cellular matter are formed from the amino acids contained in the
medium but while using thek salt medium these chains should be
synthesized entirely from the main substrate.
3

The energetic yield is much higher in the rich medium with respect to
the salts medium since the cellular material synthesis requires a smaller
consumption because the rich medium contains several amino acids
basic for protein synthesis.
conclusions
The chemically structured model is capable of expalining the
cellular growth and consumption of sunstrate uptake in the
yeast
The model may simulate a range of metabolic responses obtained
from the T. Variabilis growth in discontinuous culture and can
serve to understand the behavior of the yeast under different
growth conditions.
Reference



Barford, J. P. A general model for aerobic yeast growth.
Biotechnol. Bioeng.1990, 35, 907-920.
Montes, F. J., Moreno, J.A., Catalan, J., and Galan, M.A.
Oxygen kinetic and metabolic parameters for the yeast
Trigonopsis Variabilis. J. Chem. Tech.
Biotechnol.1997,68,243-246.
Montes F.J., Catalan J., and Galan M.A. Barford, J. P. A
metabolic model describing growth and substrate uptake of
Trigonopsis Variabilis. Enzyme and Microbial Technol.
1998, 22, 329-334.