Download Very brief introduction to Conformal Field Theory

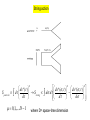
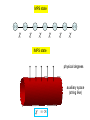
Germán Sierra
Instituto de Física Teórica CSIC-UAM, Madrid
Talk at the 4Th GIQ Mini-workshop February 2011
-String theory
-Critical phenomena in 2D Statistical Mechanics
-Low D-strongly correlated systems in Condensed Matter
-Fractional quantum Hall effect
-Quantum information and entanglement

s-channel
t-channel


p1  p2  p3  p4


Mandelstam variables
Scattering amplitude
u-channel

s  ( p1  p2 ) 2

t  (p  p )
1
2
3
u  ( p1  p4 ) 2

A  A(s,t,u)


( (s))( (t))
A(s,t) 

( (s)   (t))
 dx x 
 (s)1
(1 x) (t )1
0
(s)  s  (0)
Regge trayectory

1
q

q

s-t duality

q

q
String action
dx  ( ) 2
S particle   d 
  Sstring 
 d 
  0,1,
D 1
dx  ( ,  ) 2 dx  ( ,  ) 2
 d d d    d  


where D= space-time dimension
A(s,t)   D x( ,  )e
Sstring
 d e
i p1 x  ( 1 ,)
1
 d e
i p 4 x  ( ,)
4
x  ( ,  ) is a 1+1 field that satisfies the equations of motion
 d 2
d 2  



 2  2 x ( ,  )  0  x ( ,  )  x R (   )  x L (   )
d 
d
Open

dx  ( ,  )
1



 0,   0,   x ( ,  )  x  p   i   n ei n  cos n
d
n n

Closed

1
x  (0,  )  x  (2 ,  )  x  ( ,  )  x   p   i  ( n e2i n (  ) n e2i n (  ) )
n n

Quantization
x , p  i
 ,  n 




n
m
 ,
,
n m,0
  , ,
 ,  n 


n
m
n m,0
 , ,


n
,m  0
String=zero modes (x,p)+infinite number of harmonic oscillators
Vertex operators: insertions of particles on the world-sheet
(Fubini and Veneziano 1970)








i k x(0, )
i
n

i
k(x

p

)
i
n

:e
:expk   n e e
expk   n e 
 n1 n

 n1 n

The energy-momentum tensor
Generator of motions on the string world-sheet
Tab (, ) (a,b  0,1)
T is a symmetric, conserved and traceless tensor
Tab  Tba ,  a Tab  0,  ab Tab  0
For closed string T splits into left and right components
 In light cone variables
1
    ,   (   )
2

1
T  (T00  T01)   x    x 
2
1

T  (T00  T01)   x   x 
2
Virasoro operators
Make the Wick rotation
  ,    z    i , z    i
Fourier expansion of the energy momentum tensor
T  Tzz (z) 

L
n2
z
n
n
T  Tz z (z ) 

n2
L
z
 n
n
Where Ln , Ln (n  Z) are called the Virasoro operators


Ln 
1
1


,
L

nm m ,


nm m
n
2 m
2 m
Virasoro algebra
The Virasoro operators satisfy the algebra
Ln ,Lm   (n  m) Ln m 
c 3
(n  n)n m,0
12
where c = central charge of the Virasoro algebra

Classical version of the Virasoro algebra

n
,
m
  (n  m)
n m
,
n
 z
n 1

z
This contains the conformal transformations of the plane:
1
 z
translations
0
 z  z
dilatations
2

z
z
1
special conformal
z  z
az  b
,
cz d
ad  bc  1

In 2D the conformal group is infinite dimensional !!
n
(n  Z)
Ln (n  Z)
Classical generators of conformal transformations
Quantum generators of conformal transformations
“c” represents an anomaly of conformal transformations
Physical meaning of “c”
Bosonic string: X-fields + Faddev-Popov ghost
c =
D
- 26
Superstring: X-fields + fermionic fields + Faddev Popov ghost
c = D
+ D/2
- 26 + 11 = 3D/2 -15
String theory does not have a conformal anomaly!!
c = 0 -> D = 26 (bosonic string) and 10 (superstring)
c gives a measure of the total degrees of freedom in CFT
c= 1 (boson)
c= 1/2 (Majorana fermion/Ising model)
c= 1 (Dirac fermion/1D fermion)
c= 3/2 (boson+Majorana or 3 Majoranas)
c=….
Fractional values of c reflect highly non perturbative effects
The Belavin-Polyakov-Zamolodchikov (1984)
Infinite conformal symmetry in two-dimensional quantum field theory
Conformal transformations
z  w  f (z),
z  w  f (z )

Covariant tensors are characterized by two numbers
h, h

Conformal weights
h h (z,z )(dz)h (dz )h  hh (w,w)(dw)h (dw)h
A (x) dx   A( x ) dx  Az (z)dz (h 1,h  0)  Az (z )dz (h  0,h 1)


Dilation
zz
wwz,z, zz
wwzz (
(: :real)
real)

General framework of CFT
-T is a symmetric, conserved and traceless tensor
with central charges c  c (no need of an action)
- There is a vacuum state |0> which satisfies
Ln 0 
 Ln 0  0,
n  1,0,1,2,

-There is an infinite number of conformal fields
in one-to-one correspondence with the states

(z,z ) 
  lim   ( ,  ) 0  lim z 0 (z,z ) 0
-There are special fields (and states) called primary satisfying
L0 h,h  h h,h , L0 h,h  h h,h
Ln h,h  0, Ln h,h  0, n  0
T (x)dx  dx   T ( x )dx  dx  Tzz (z) (dz)2 (h  2,h  0)  Tz (z )dz (h  0,h  2)
-The remaing fields form towers obtained from the primary fields
acting with the Virasoro operators (they are called descendants)
h
L1  h
Verma
module:
L21  h ,L2  h
L31  h ,L1L2  h ,L3  h
L0
h
h 1
h2
h3
-The primary fields form a close operator product expansion algebra
For chiral (holomorphic
 fields)
OPE
i
k 
j

 i (z)  j (w)  
Cijk
hi h j hk
constants
 k (w) 
(z  w)
c /2
2T(w) T(w)
T(z) T(w) 



4
2
(z  w)
(z  w) (z  w)
k
- Fusion rules (generalized Clebsch-Gordan decomposition)
c
c
a  b   N ab
k , N ab
 0,1,
k
- Rational Conformal Field Theories (RCFT): finite nº primary fields
- 
Minimal models
c  1
6
, m  3,4,
m(m  1)
(m  1)r  ms


2
hr,s
4m(m  1)
1
, 1  r  m, 1  s  r
A well known case is the Ising model c=1/2 (m=3)

I  1,1 or  2,3,
h0  0
  2,1 or 1,3, h  1/2
  2,2 or 1,2, h  1/16
   I
   
   I 
- Conformal invariance determines uniquely the 2 and 3-point correlators

i (z1 )  j (z2 ) 
i (z1 )  j (z2 ) k (z3 ) 

ij
normalization
hi h j
12
z
Cijk
hi h j hk
12
z
hi hk h j
13
z
z
h j hk hi
23
- Higher order chiral correlators: their number given by the fusion rules
Conformal blocks for the Ising model
Fusion rules
        (I   )  (I   )  I 2   (2)
There are four conformal blocks:

FI   (z1)
 (z4 ) I  2
1/ 2
z 
1/ 8
ab
z13 z24  z14 z23

z13 z24  z14 z23

1/ 2
ab
F   (z1)
 (z4 )   2
1/ 2
z 
1/ 8
ab
1/ 2
ab
The non-chiral correlators (the ones in Stat Mech)

 (z1,z1)  (z4 ,z4 )  FI z1, z4 FI* z1, z4   F z1, z4 F* z1, z4 
Must be invariant under
Braiding of coordinates
z1
z2
z3
z4
Conformal blocks give a representation of the Braid group
Fp 
zi zi1
  B

p,q
Fq 
zi1 zi

q
Yang-Baxter equation

Related to polynomials for knots and links, Chern-Simon theory,
Anyons, Topological Quantum Computation, etc

Characters and modular invariance
a
Conformal tower of a primary field
 a ( )  TrH qL c / 24  qc / 24  da (n)
0
a
n0
da (n) : number of states at level n=0,1,2,…
q  ei ,  


Upper half of the complex plane
Moduli
 parameter of the torus
0
 1
1
states propagation
Modular group
Fundamental region
a   b a b 

, 
 Sl(2,Z) :
c   d c d 
Generators
T :   1
S :   1/ 
Characters transforms under modular transformations as

 a (  1)  e i(h
a
c / 24)
 a ( )
 a (1/  )  b Sab  b ( )
Partition function of CFT must be modular invariant
L 0 c / 24 L 0 c / 24
Z(

)

Tr
q
q
  M ab  a ( )  a ()

H
a,b
Z( )  Z(  1)  Z(1/  )
Verlinde formula (1988)
Fusion matrices and S-matrix and related!!
*
S
S
S
c
N ab
  am bm cm
S1m
m
Example: Ising model

 1
1
2 

1 
S   1
1
 2 
2 
0 
 2  2

Check



N
I


2
2
1 



2   2  01

4 
   
Axiomatic of CFT
Moore and Seiberg (1988-89)
- Algebra: Chiral  antichiral  Virasoro left  right ( c ) + others
- Representation: primary fields  a ,

- Fusionrules:
c
N ab
ha ,ha

- B and F matrices : BBB
 =BBB (Yang-Baxter) FF = FFF (pentagonal)
- Modular matrices T and S

Sort of generalization of group theory-> Quantum Groups
Wess-Zumino-Witten model (1971-1984)
CFT with “colour”
Field is an element of a Group manifold
SW ZW 
k
16
2
 1
d
x
Tr


 g  g
Conformal invariance->
ik
24
g(z,z )  G
3
1  1 1  1 1  1
d
y

Tr
g

 g g g gg 


g(z,z )  f (z) f (z )
B
Currents
J a (z)  k z g g1   J na zn1

n
J a (z )  k g1z g  J na z n1
n
a  1, ,dim G
OPE of currents
k ab
J c (w)
J (z) J (w) 
  i f abc

2
(z  w)
zw
c
a
b
Kac-Moody algebra (1967)

a
b
c
J
,J

i
f
J
 n m   abc n m  k n ab n m,0
k= level (entero)
c
Sugawara construction (1967)
 T(z) 
Ln 
1
J a (z) J a (z)

2(k  g) a
1
a
: Jnm
Jma :


2(k  g) a m
c
k dim G
kg
g: dual Coxeter number of G
Primary fields and fusion rules (Gepner-Witten 1986)
1
k
j  0, , ,
2
2
G=SU(2)

j j 
1
2
min  j1  j 2 ,k j1  j 2 

j
j j1  j 2
Knizhnik- Zamolodchikov equations (1984)

N

Si  S j

(k  g)

 zi ji zi  z j



  j1 (z1 )


 j (zN )  0
N
Heisenberg-Bethe spin 1/2 chain
H   Sn  Sn 1
n
Low energy physics is described by the WZW SU(2)@k=1

Si  S j (1)
i j
log i  j
i j
But the spin 1 chain is not a CFT (Haldane 1983)

Si  S j  (1) i j e i j /
-> Haldane phase and gap
FQHE/CFT correspondence
Laughlin wave function
 (z1, zN )  (zi  z j ) m e
 zk 2 / 4

i j
i
quasihole ->
 (z)e 2
2
 (z)

Basis for Topological Quantum 
Computation
(braids -> gates)
electron =
 (z)e i
2  (z)
The entanglement entropy in a bipartition A U B scales as
SA log 
(1D area law)
In a critical system described by a CFT (periodic BCs)

c
SA  log L  c1
3
hence one needs very large matrices to describe critical systems

N   ,
   (c)
Another alternative is to choose infinite dimensional matrices:

 
MPS state






iMPS state






physical degrees
auxiliary space
(string like)
 
Example 5: level k=2, spins =1/2 and 1, D=2
SU(2)@2 = Boson + Ising
c=3/2 = 1 + 1/2
spin j=1 field
spin j=1/2 field
1,1(z)  e
i (z)
, 1,0 (z)  (z),
1/ 2,1/ 2 (z)   (z)e
i (z)/ 2

1
h1  h 
2
1
, h  ,
16
3
h1/ 2 
16
The chiral correlators can be obtained from those of the Ising model

(general formula Ardonne-Sierra 2010)
N spins 1
  s1,, ,sN    s i j zi  z j 
si s j
 1 
Pf 0
z  z 

 i
j 
The Pfaffian comes from the correlator of Majorana fields
Similar chiral correlators have been considered in
the Fractional Quantum Hall effect at filling fraction 5/2.
This is the so called Pfaffian state due to Moore and Read.
FQHE/CFT correspondence
electron =
 (z)e
i 2  (z)
i
quasihole ->
 (z)e 2
2
 (z)
Quasiholes are non abelian anyons because their wave
functions (chiral correlators) mix under braiding of their positions.
Computation
Basis for Topological Quantum 
(braids -> gates)
An analogy via CFT
FQHE
CFT
Spin Models
Electron
Quasihole
Majorana
 field
spin 1
spin 1/2
Braid of
quasiholes
Monodromy
of correlators
Adiabatic
change of H

Then if Holonomy = Monodromy one could get
Topological Quantum Computation in the FQHE and
the Spin Models.
Bibliography
Applied Conformal Field Theory
Paul Ginsparg,
arXiv:hep-th/9108028
Non-Abelian Anyons and Topological Quantum Computation
C. Nayak, S. H. Simon, A. Stern, M. Freedman, S. Das Sarma,
arXiv:0707.1889