Quantum field theory correlators at very short and very long distances
... geometry! As in QFT in flat spacetime, one is interested at the end of the day in the redcorrelation functions: hO1 (x1 ) . . . On (xn )iΨ , where Oi are local (composite) fields in the theory, evaluated at spacetime points xi Ψ is a quantum state As in flat space, general form of correlation is res ...
... geometry! As in QFT in flat spacetime, one is interested at the end of the day in the redcorrelation functions: hO1 (x1 ) . . . On (xn )iΨ , where Oi are local (composite) fields in the theory, evaluated at spacetime points xi Ψ is a quantum state As in flat space, general form of correlation is res ...
Geometry
... be represented by a recursive definition When using a fractal to represent a physical object, some degree of randomness is usually added to make the image more realistic groups that have broken dimensions so that each one looks like an exact copy of the second (like the 8 Mandelbrot group in Mathema ...
... be represented by a recursive definition When using a fractal to represent a physical object, some degree of randomness is usually added to make the image more realistic groups that have broken dimensions so that each one looks like an exact copy of the second (like the 8 Mandelbrot group in Mathema ...
String Theory. Volume 1, Introduction to the Bosonic String
... and many important aspects of string physics, such as T-duality and D-branes. Chapter nine treats higher-order amplitudes, including an analysis of the finiteness and unitarity, and various nonperturbative ideas. An appendix giving a short course on path integral methods is also included. Volume II, ...
... and many important aspects of string physics, such as T-duality and D-branes. Chapter nine treats higher-order amplitudes, including an analysis of the finiteness and unitarity, and various nonperturbative ideas. An appendix giving a short course on path integral methods is also included. Volume II, ...
Introduction to Lattice Field Theory
... Fourier transforms and the Brillouin zone In practice our lattice will not be infinite, but a finite hypercube with, say, N D sites. At each site, x, on the lattice, let us put a complex number φ(x). We can put periodic boundary conditions, φ(x) = φ(x + µ̂N). Next, we can make Fourier transforms X 1 ...
... Fourier transforms and the Brillouin zone In practice our lattice will not be infinite, but a finite hypercube with, say, N D sites. At each site, x, on the lattice, let us put a complex number φ(x). We can put periodic boundary conditions, φ(x) = φ(x + µ̂N). Next, we can make Fourier transforms X 1 ...
On the Theory of Generalized Algebraic Transformations
... as the purely academic model without any correspondence to a specific real-world system, since the first insulating magnetic materials that would satisfy its specific requirements have been discovered almost a half century after its invention. At present, there are two wide families of insulating ma ...
... as the purely academic model without any correspondence to a specific real-world system, since the first insulating magnetic materials that would satisfy its specific requirements have been discovered almost a half century after its invention. At present, there are two wide families of insulating ma ...
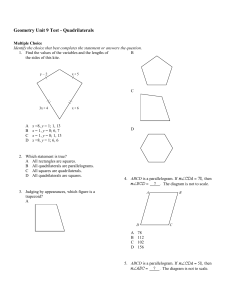
Geometry Unit 9 Test - Quadrilaterals
... 17. The isosceles trapezoid is part of an isosceles triangle with a 22° vertex angle. What is the measure of an acute base angle of the trapezoid? Of an obtuse base angle? The diagram is not to scale. ...
... 17. The isosceles trapezoid is part of an isosceles triangle with a 22° vertex angle. What is the measure of an acute base angle of the trapezoid? Of an obtuse base angle? The diagram is not to scale. ...
Modeling Geometric Figures
... in a scale drawing is related to the actual object. Scales are usually shown as two numbers separated by a colon such as 1:20 or 1 cm:1 m. Scales can be shown in the same unit or in different units. You can solve scale-drawing problems by using proportional reasoning. ...
... in a scale drawing is related to the actual object. Scales are usually shown as two numbers separated by a colon such as 1:20 or 1 cm:1 m. Scales can be shown in the same unit or in different units. You can solve scale-drawing problems by using proportional reasoning. ...
Landau`s Fermi Liquid Theory
... The free, i.e. non-interacting, Fermi gas give basic understanding of both cold Fermi systems. In particular, adding neutralizing or confining potentials it gives a qualitative understanding of Specific heat of (many) metals at low temperature The formation of neutron stars Adding a periodic potenti ...
... The free, i.e. non-interacting, Fermi gas give basic understanding of both cold Fermi systems. In particular, adding neutralizing or confining potentials it gives a qualitative understanding of Specific heat of (many) metals at low temperature The formation of neutron stars Adding a periodic potenti ...
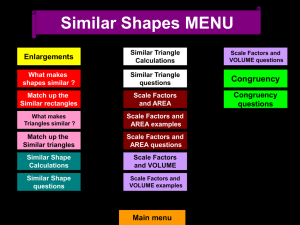
Similar Shapes 1
... Fully describe each Enlargement : Give the Scale Factor and the coordinates of the Centre of Enlargement (Each square = 1 unit) ...
... Fully describe each Enlargement : Give the Scale Factor and the coordinates of the Centre of Enlargement (Each square = 1 unit) ...
Quantum Field Theory in Condensed Matter Physics 2nd Ed.
... The general strategy of the book is to show how the strong interaction arises in various parts of QFT. I do not discuss in detail all the existing condensed matter theories where it occurs; the theories of localization and quantum Hall effect are omitted and the theory of heavy fermion materials is ...
... The general strategy of the book is to show how the strong interaction arises in various parts of QFT. I do not discuss in detail all the existing condensed matter theories where it occurs; the theories of localization and quantum Hall effect are omitted and the theory of heavy fermion materials is ...
Scale invariance

In physics, mathematics, statistics, and economics, scale invariance is a feature of objects or laws that do not change if scales of length, energy, or other variables, are multiplied by a common factor. The technical term for this transformation is a dilatation (also known as dilation), and the dilatations can also form part of a larger conformal symmetry.In mathematics, scale invariance usually refers to an invariance of individual functions or curves. A closely related concept is self-similarity, where a function or curve is invariant under a discrete subset of the dilatations. It is also possible for the probability distributions of random processes to display this kind of scale invariance or self-similarity.In classical field theory, scale invariance most commonly applies to the invariance of a whole theory under dilatations. Such theories typically describe classical physical processes with no characteristic length scale.In quantum field theory, scale invariance has an interpretation in terms of particle physics. In a scale-invariant theory, the strength of particle interactions does not depend on the energy of the particles involved.In statistical mechanics, scale invariance is a feature of phase transitions. The key observation is that near a phase transition or critical point, fluctuations occur at all length scales, and thus one should look for an explicitly scale-invariant theory to describe the phenomena. Such theories are scale-invariant statistical field theories, and are formally very similar to scale-invariant quantum field theories.Universality is the observation that widely different microscopic systems can display the same behaviour at a phase transition. Thus phase transitions in many different systems may be described by the same underlying scale-invariant theory.In general, dimensionless quantities are scale invariant. The analogous concept in statistics are standardized moments, which are scale invariant statistics of a variable, while the unstandardized moments are not.












![[edit] Construction of the Lebesgue measure](http://s1.studyres.com/store/data/001141507_1-534aa5aeea25b32a8226835f0ebc16e0-300x300.png)