* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Landau`s Fermi Liquid Theory
Quasi-set theory wikipedia , lookup
Standard Model wikipedia , lookup
Quantum logic wikipedia , lookup
Quantum chaos wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
Quantum chromodynamics wikipedia , lookup
Mathematical formulation of the Standard Model wikipedia , lookup
Quantum field theory wikipedia , lookup
Nuclear structure wikipedia , lookup
Old quantum theory wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Scale invariance wikipedia , lookup
Relational approach to quantum physics wikipedia , lookup
Canonical quantization wikipedia , lookup
Quantum gravity wikipedia , lookup
AdS/CFT correspondence wikipedia , lookup
Theory of everything wikipedia , lookup
Renormalization group wikipedia , lookup
Yang–Mills theory wikipedia , lookup
Topological quantum field theory wikipedia , lookup
Renormalization wikipedia , lookup
Scalar field theory wikipedia , lookup
Landau’s Fermi Liquid Theory
Thors Hans Hansson
Stockholm University
Quantum Field Theory for Condensed Matter
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Outline
1
Fermi Liquids – Why, What, and How?
Why Fermi liquids?
What is a Fermi liquids?
Fermi Liquids – How?
2
Landau’s Phenomenological Approach
The free Fermi gas
Landaus basic idea
The Energy Functional E [n(p)]
The effective mass
The quasiparticle Fermi surface
When can Fermi Liquid theory be used?
Quasiparticle interactions
3
Renormalization Group approach to FL theory
An RG primer
Fermi Liquids as a RG fixed point
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Next subject
1
Fermi Liquids – Why, What, and How?
Why Fermi liquids?
What is a Fermi liquids?
Fermi Liquids – How?
2
Landau’s Phenomenological Approach
The free Fermi gas
Landaus basic idea
The Energy Functional E [n(p)]
The effective mass
The quasiparticle Fermi surface
When can Fermi Liquid theory be used?
Quasiparticle interactions
3
Renormalization Group approach to FL theory
An RG primer
Fermi Liquids as a RG fixed point
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Fermi liquids - Why do we want it?
The free, i.e. non-interacting, Fermi gas give basic understanding of both
cold Fermi systems. In particular, adding neutralizing or confining
potentials it gives a qualitative understanding of
Specific heat of (many) metals at low temperature
The formation of neutron stars
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Fermi liquids - Why do we want it?
The free, i.e. non-interacting, Fermi gas give basic understanding of both
cold Fermi systems. In particular, adding neutralizing or confining
potentials it gives a qualitative understanding of
Specific heat of (many) metals at low temperature
The formation of neutron stars
Adding a periodic potential, the band theory of non-interacting electrons
also explains
Conductors – semiconductors – metals
Shape of Fermi surface and related spectroscopy
The success of this ridiculously oversimplified model is not a coincidence.
The theory of Fermi Liquids provides an explanation.
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Fermi liquids - Why do we want it?
The concept of a Fermi Liquid describes (strongly) interacting fermions
using concepts that naively would only be applicable to a very weakly
interacting gas. That this is at all possible makes Fermi Liquid theory a
very versatile, but at the same time its very success is puzzling.
Fermi Liquid theory is:
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Fermi liquids - Why do we want it?
The concept of a Fermi Liquid describes (strongly) interacting fermions
using concepts that naively would only be applicable to a very weakly
interacting gas. That this is at all possible makes Fermi Liquid theory a
very versatile, but at the same time its very success is puzzling.
Fermi Liquid theory is:
Is simple to use
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Fermi liquids - Why do we want it?
The concept of a Fermi Liquid describes (strongly) interacting fermions
using concepts that naively would only be applicable to a very weakly
interacting gas. That this is at all possible makes Fermi Liquid theory a
very versatile, but at the same time its very success is puzzling.
Fermi Liquid theory is:
Is simple to use
Is a good approximation to weakly interacting (dilute)
Fermi systems
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Fermi liquids - Why do we want it?
The concept of a Fermi Liquid describes (strongly) interacting fermions
using concepts that naively would only be applicable to a very weakly
interacting gas. That this is at all possible makes Fermi Liquid theory a
very versatile, but at the same time its very success is puzzling.
Fermi Liquid theory is:
Is simple to use
Is a good approximation to weakly interacting (dilute)
Fermi systems
Gives a remarkably good description of real metals
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Fermi liquids - Why do we want it?
The concept of a Fermi Liquid describes (strongly) interacting fermions
using concepts that naively would only be applicable to a very weakly
interacting gas. That this is at all possible makes Fermi Liquid theory a
very versatile, but at the same time its very success is puzzling.
Fermi Liquid theory is:
Is simple to use
Is a good approximation to weakly interacting (dilute)
Fermi systems
Gives a remarkably good description of real metals
But how can that be??
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Next subject
1
Fermi Liquids – Why, What, and How?
Why Fermi liquids?
What is a Fermi liquids?
Fermi Liquids – How?
2
Landau’s Phenomenological Approach
The free Fermi gas
Landaus basic idea
The Energy Functional E [n(p)]
The effective mass
The quasiparticle Fermi surface
When can Fermi Liquid theory be used?
Quasiparticle interactions
3
Renormalization Group approach to FL theory
An RG primer
Fermi Liquids as a RG fixed point
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Fermi liquids - What is it?
Fermi liquid theory describe a strongly interacting Fermi system, such as
nuclear matter, liquid Helium III, or electrons interacting via Coulomb
forces. The basic concepts/ideas in Fermi liquid theory (of electrons) are:
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Fermi liquids - What is it?
Fermi liquid theory describe a strongly interacting Fermi system, such as
nuclear matter, liquid Helium III, or electrons interacting via Coulomb
forces. The basic concepts/ideas in Fermi liquid theory (of electrons) are:
Weakly interacting quasielectrons and quasiholes
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Fermi liquids - What is it?
Fermi liquid theory describe a strongly interacting Fermi system, such as
nuclear matter, liquid Helium III, or electrons interacting via Coulomb
forces. The basic concepts/ideas in Fermi liquid theory (of electrons) are:
Weakly interacting quasielectrons and quasiholes
The quasiparticles have the same quantum numbers as electrons and
holes, i.e. momentum ~k, spin 12 and charge ±e.
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Fermi liquids - What is it?
Fermi liquid theory describe a strongly interacting Fermi system, such as
nuclear matter, liquid Helium III, or electrons interacting via Coulomb
forces. The basic concepts/ideas in Fermi liquid theory (of electrons) are:
Weakly interacting quasielectrons and quasiholes
The quasiparticles have the same quantum numbers as electrons and
holes, i.e. momentum ~k, spin 12 and charge ±e.
The state of the Fermi liquid is described as a collection of n
quasiparticles, |~k1 , α1 . . . ~kN , αN i
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Fermi liquids - What is it?
Fermi liquid theory describe a strongly interacting Fermi system, such as
nuclear matter, liquid Helium III, or electrons interacting via Coulomb
forces. The basic concepts/ideas in Fermi liquid theory (of electrons) are:
Weakly interacting quasielectrons and quasiholes
The quasiparticles have the same quantum numbers as electrons and
holes, i.e. momentum ~k, spin 12 and charge ±e.
The state of the Fermi liquid is described as a collection of n
quasiparticles, |~k1 , α1 . . . ~kN , αN i
The interaction between the quasiparticles is described by a few Fermi
liquid parameters fl .
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Fermi liquids - What is it?
Fermi liquid theory describe a strongly interacting Fermi system, such as
nuclear matter, liquid Helium III, or electrons interacting via Coulomb
forces. The basic concepts/ideas in Fermi liquid theory (of electrons) are:
Weakly interacting quasielectrons and quasiholes
The quasiparticles have the same quantum numbers as electrons and
holes, i.e. momentum ~k, spin 12 and charge ±e.
The state of the Fermi liquid is described as a collection of n
quasiparticles, |~k1 , α1 . . . ~kN , αN i
The interaction between the quasiparticles is described by a few Fermi
liquid parameters fl .
At finite temperature and chemical potential, the state of a Fermi
Liquid is given by a density matrix for the quasiparticles, and there is
a corresponding kinetic theory based on the distribution function f .
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Next subject
1
Fermi Liquids – Why, What, and How?
Why Fermi liquids?
What is a Fermi liquids?
Fermi Liquids – How?
2
Landau’s Phenomenological Approach
The free Fermi gas
Landaus basic idea
The Energy Functional E [n(p)]
The effective mass
The quasiparticle Fermi surface
When can Fermi Liquid theory be used?
Quasiparticle interactions
3
Renormalization Group approach to FL theory
An RG primer
Fermi Liquids as a RG fixed point
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Fermi Liquids – How?
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Fermi Liquids – How?
I will now describe Landaus intuitive approach to Fermi liquids, based
on adiabatic evolution from the free Fermi gas.
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Fermi Liquids – How?
I will now describe Landaus intuitive approach to Fermi liquids, based
on adiabatic evolution from the free Fermi gas.
Later a diagrammatic approach was used to derive Fermi Liquid
theory, but this is rather complicated and is based on resuming
infinite classes of diagrams.
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Fermi Liquids – How?
I will now describe Landaus intuitive approach to Fermi liquids, based
on adiabatic evolution from the free Fermi gas.
Later a diagrammatic approach was used to derive Fermi Liquid
theory, but this is rather complicated and is based on resuming
infinite classes of diagrams.
The modern Renormalization Group approach to Fermi Liquid theory,
due primarily to Shankar and Polchinski, defines the Fermi Liquid as a
fixed point of the RG flow. This roughly means that the FL
description is what is left when all the high energy degrees of freedom
are integrated out.
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Next subject
1
Fermi Liquids – Why, What, and How?
Why Fermi liquids?
What is a Fermi liquids?
Fermi Liquids – How?
2
Landau’s Phenomenological Approach
The free Fermi gas
Landaus basic idea
The Energy Functional E [n(p)]
The effective mass
The quasiparticle Fermi surface
When can Fermi Liquid theory be used?
Quasiparticle interactions
3
Renormalization Group approach to FL theory
An RG primer
Fermi Liquids as a RG fixed point
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
The free Fermi gas
For a gas of free fermions with mass me , the zero temperature ground
state is obtained by filling all single particle (plane wave) states up to the
Fermi energy F . With the T = 0 distribution function
n0 (~
p ) = θ(|~
p | − pF ) we get,
Total energy
ˆ
d 3p
E = V Tr
(p)n0 (p)
(2π)3
ˆ
VpF2
p2
V p5
≡ Tr dτ
n0 (p) = 2 F =
F
2me
5π 2me
5π 2
where V is the, (p) =
p2
2me ,
F = (pF ), and
ˆ
ˆ
X
d 3p
dτ = V
=
(2π)3
~
ki
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
The free Fermi gas
Total number of particles
ˆ
N=
dτ n0 (p) = V
pF3
3π 2
Excitations from the ground state is obtained by changing the occupation
numbers of the single particle levels, i.e. by changing the distribution
function,
n(p) = θ(p − pF ) + δn(p)
For discrete momentum states, δn can only take the values ±1 because of
the Pauli principle.
The distribution function at finite temperature T is determined by
maximizing the entropy,
ˆ
S = − dτ [n(p) ln n(p) + (1 − n(p)) ln(1 − n(p))]
under the constraints δE = δN = 0 to get:
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
The free Fermi gas
Finite T Fermi-Dirac distribution function
nβ (p) =
1
e β((p)−F )
+1
,
β=
1
kT
Note that no dynamical information was needed - only that the particles
are fermions.
These considerations can be generalized to include an external potential,
but in those cases the integrals can in general not be calculated on a
closed form and there are no analytical expression for energy, entropy etc.
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Next subject
1
Fermi Liquids – Why, What, and How?
Why Fermi liquids?
What is a Fermi liquids?
Fermi Liquids – How?
2
Landau’s Phenomenological Approach
The free Fermi gas
Landaus basic idea
The Energy Functional E [n(p)]
The effective mass
The quasiparticle Fermi surface
When can Fermi Liquid theory be used?
Quasiparticle interactions
3
Renormalization Group approach to FL theory
An RG primer
Fermi Liquids as a RG fixed point
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Landaus basic idea
Landau’s basic idea was that the interacting system can be thought of as
”connected” to the free fermi gas by an adiabatic switching process. In
particular, this means
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Landaus basic idea
Landau’s basic idea was that the interacting system can be thought of as
”connected” to the free fermi gas by an adiabatic switching process. In
particular, this means
there is an one-one correspondence between the excitations in the free
and the interacting system.
For a state with one fermion added to the ground state, this means
|~
p , αifree → |~
p , αiint.
The quantum numbers charge q, momentum p~, and spin α of the
quasiparticle remain the same, but the energy is changed
There is a Fermi surface also in the interacting system
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Next subject
1
Fermi Liquids – Why, What, and How?
Why Fermi liquids?
What is a Fermi liquids?
Fermi Liquids – How?
2
Landau’s Phenomenological Approach
The free Fermi gas
Landaus basic idea
The Energy Functional E [n(p)]
The effective mass
The quasiparticle Fermi surface
When can Fermi Liquid theory be used?
Quasiparticle interactions
3
Renormalization Group approach to FL theory
An RG primer
Fermi Liquids as a RG fixed point
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
The Energy Functional E [n(p)]
When interactions are present the total energy still depends on the
distribution function, n(p) but this functional dependence is very
complicated. We are however only interested in the change in energy as
we vary the occupation numbers:
Variation of E [n]
ˆ
δE [n(p)] =
1
dτ 0 (p)δn(p) +
2V
ˆ
dτ dτ 0 f (~
p , p~0 )δn(p)δn(p 0 ) + . . .
where V is the volume of the system,
0 (p) =
and
f (~
p , p~0 ) =
Thors Hans Hansson (Stockholm University)
δE [n]
|n=n0
δn(p)
δ 2 E [n]
|n=n0
δn(p)δn(p 0 )
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
The quasiparticle distribution function
Since the entropy follows from a counting argument, and since there is an
one-one correspondence between the states in the interacting and the
non-interacting system, the calculation of the entropy will look precisely
the same, except that the constraint δE = 0 now becomes,
ˆ
dτ 0 [n, p]δn(p) = 0 ,
Minimizing the entropy under this constraint gives,
Functional equation for the quasiparticle distribution function
nβ (p) =
1
e β([n,p]−F )
+1
.
which is a very complicated functional equation.
From the previous arguments we however know that it will approach
n0 (p) = θ(p − pF ) as T goes to zero.
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
The effective mass m? I - definition
Now we assume that the temperature is low enough that we can put
n(p) = θ(p − pF ) and expand around the Fermi momentum,
[n(p 0 ), p] ≈ [θ(p − pF ), p] ≈ F + vF (p − pF ) + . . .
To understand the meaning of F and vF , recall that pF is the same as in
the free theory, but the Fermi energy is not. But [n, p] is the energy cost
for adding a single quasiparticle, so F = µ = chemical potential
For the non-interacting gas,
(p) = F +
pF
(p − pF ) + . . . .
me
From this we conclude
vF = Fermi velocity =
pF
pF
6=
m?
me
This relation defines the effective mass m? .
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Next subject
1
Fermi Liquids – Why, What, and How?
Why Fermi liquids?
What is a Fermi liquids?
Fermi Liquids – How?
2
Landau’s Phenomenological Approach
The free Fermi gas
Landaus basic idea
The Energy Functional E [n(p)]
The effective mass
The quasiparticle Fermi surface
When can Fermi Liquid theory be used?
Quasiparticle interactions
3
Renormalization Group approach to FL theory
An RG primer
Fermi Liquids as a RG fixed point
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
The effective mass m? II - how to measure
One of the simplest observables that can be measured for a Fermi liquid is
its specific heat, cV .
It is the same as for the free electron gas with the substitution me → m? ,
cV =
m? pF 2
kB T ,
3
The effective mass can vary a lot:
3 He
Heavy fermion compounds such as
Thors Hans Hansson (Stockholm University)
UPt3
m? /me ≈ 3
m? /me ≈ 100 − 1000
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Next subject
1
Fermi Liquids – Why, What, and How?
Why Fermi liquids?
What is a Fermi liquids?
Fermi Liquids – How?
2
Landau’s Phenomenological Approach
The free Fermi gas
Landaus basic idea
The Energy Functional E [n(p)]
The effective mass
The quasiparticle Fermi surface
When can Fermi Liquid theory be used?
Quasiparticle interactions
3
Renormalization Group approach to FL theory
An RG primer
Fermi Liquids as a RG fixed point
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Meaning of the quasiparticle Fermi surface
At zero temperature, the quasiparticle distribution function n(p) is sharp
(dotted line).
The momentum distribution of the electrons, N(p) = hΨFL |cp† cp |ΨFL i
Z is the wave function renormalization constant, or the strength of the
single particle pole.
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Next subject
1
Fermi Liquids – Why, What, and How?
Why Fermi liquids?
What is a Fermi liquids?
Fermi Liquids – How?
2
Landau’s Phenomenological Approach
The free Fermi gas
Landaus basic idea
The Energy Functional E [n(p)]
The effective mass
The quasiparticle Fermi surface
When can Fermi Liquid theory be used?
Quasiparticle interactions
3
Renormalization Group approach to FL theory
An RG primer
Fermi Liquids as a RG fixed point
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
When is FL theory applicable?
A quasielectron at a momentum p~1 it can decay into two quasielectrons
and one quasihole,
|~
p1 i− → |~
p2 i− + |~
p3 i− + |~
p2 − p~1 − p~3 i+
This makes the quasiparticles unstable !!!
Landau’s fundamental observation
Close to the Fermi surface, the phase space for decay vanish ∼ |~
p − p~F |2
and the quasiparticles become almost stable!!
In fact, the life time τ becomes
τ=
1
∼ |~
p − p~F |−2
Γ
For FL theory to be applicable, we must have T TF
TF for metallic sodium is ≈ 40, 000K but for liquid He3 only ≈ 7K !!
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Next subject
1
Fermi Liquids – Why, What, and How?
Why Fermi liquids?
What is a Fermi liquids?
Fermi Liquids – How?
2
Landau’s Phenomenological Approach
The free Fermi gas
Landaus basic idea
The Energy Functional E [n(p)]
The effective mass
The quasiparticle Fermi surface
When can Fermi Liquid theory be used?
Quasiparticle interactions
3
Renormalization Group approach to FL theory
An RG primer
Fermi Liquids as a RG fixed point
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Interactions - definition of the FL parameters
Writing out the spin indices
0
[n(p ), p]αβ
1
= 0,αβ (p) +
V
ˆ
dτ 0 f (~
p , p~0 )αγ,βδ δnγδ (p 0 ) + . . . .
f only depends on the angle θ given by p~ · p~0 = pp 0 cos θ ≈ pF2 cos θ
Symmetries (rotation, TR) and Fermi statistics implies,
f (~
p , p~0 )αγ,βδ = f (cos θ)δαβ δγδ + g (cos θ)S~αβ · S~γδ .
~ fields), we have nαβ = nδαβ , and
For an isotropic liquid (no B
ˆ
0
[n(p ), p] = F + vF (p − pF ) + dτ 0 f (cos θ)δn(p 0 )
F-parameters
∞
F (θ) =
X
pF m ?
f
(cos
θ)
=
(2L + 1)FL PL (cos θ)
π2
L=0
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Important relations
The effective mass m? is not independent of the parameters FL . In fact
m?
F1
=1+
me
3
follows from Gallilean invariance.
The compressibility κ is given by,
κ=
m? pF
π 2 ρ2 (1 + F0 )
where ρ is the density.
The response to a magnetic field involves the function g (cos θ), and the
susceptibility is determined by the parameter G0 , where GL is defined
analogously to FL
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Next subject
1
Fermi Liquids – Why, What, and How?
Why Fermi liquids?
What is a Fermi liquids?
Fermi Liquids – How?
2
Landau’s Phenomenological Approach
The free Fermi gas
Landaus basic idea
The Energy Functional E [n(p)]
The effective mass
The quasiparticle Fermi surface
When can Fermi Liquid theory be used?
Quasiparticle interactions
3
Renormalization Group approach to FL theory
An RG primer
Fermi Liquids as a RG fixed point
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Momentum cutoff
From a microscopic eucledian action S = SΛ , construct a sequence of
actions SΛn where Λn is a cutoff and the action SΛn describes the physics
for momenta p < Λn .
The first Λ can be thought of as a physical cutoff.
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Momentum cutoff
From a microscopic eucledian action S = SΛ , construct a sequence of
actions SΛn where Λn is a cutoff and the action SΛn describes the physics
for momenta p < Λn .
The first Λ can be thought of as a physical cutoff.
Study the Eucledian partition function of a φ4 theory
ˆ
Z [T , µ, . . . ] ≡ Z = D[φ, φ? ] e −S[φ]
ˆ
1 ? ~2
4
d
φ (−∇ + g2 )φ + g4 |φ| = S0 + Sint
S= d x
2
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
(1)
(2)
Quantum Field Theory for Condensed Matter
/ 39
Momentum cutoff
From a microscopic eucledian action S = SΛ , construct a sequence of
actions SΛn where Λn is a cutoff and the action SΛn describes the physics
for momenta p < Λn .
The first Λ can be thought of as a physical cutoff.
Study the Eucledian partition function of a φ4 theory
ˆ
Z [T , µ, . . . ] ≡ Z = D[φ, φ? ] e −S[φ]
ˆ
1 ? ~2
4
d
φ (−∇ + g2 )φ + g4 |φ| = S0 + Sint
S= d x
2
In Fourier space,
X
φ(~x ) =
e i p~·~x φ(~
p) =
0≤|~
p |≤Λ
X
e i p~·~x φ(~
p) +
0≤|~
p |≤Λ1
X
e i p~·~x φ(~
p)
(1)
(2)
(3)
Λ1 ≤|~
p |≤Λ
≡ φ< (~x ) + φ> (~x )
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
The effective action
The action becomes
X 1
S=
(p 2 + g2 ) φ? (~
p ) φ(~
p) +
2
0≤|~
p |≤Λ1
X
Λ1 ≤|~
p |≤Λ
1 2
(p + g2 ) φ? (~
p ) φ(~
p ) + Sint
2
= S0 [φ< ] + S0 [φ> ] + Sint [φ< , φ> ]
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
The effective action
The action becomes
X 1
S=
(p 2 + g2 ) φ? (~
p ) φ(~
p) +
2
0≤|~
p |≤Λ1
X
Λ1 ≤|~
p |≤Λ
1 2
(p + g2 ) φ? (~
p ) φ(~
p ) + Sint
2
= S0 [φ< ] + S0 [φ> ] + Sint [φ< , φ> ]
We define the effective action S eff at scale Λ1 = Λ/s by
ˆ
−S eff [φ< ]
S0 [φ< ]
=e
e
D[φ> ] e −S0 [~p> ]−Sint [φ< ,φ> ]
1
p~
φ< → ζ φ 0
s
which resets the cutoff to Λ and the kinetic term to p 2 . We then get
(suppressing the ’ s),
ˆ
h
i
eff
~ 2 + g 0 )φ + g 0 |φ|4 + g6 |φ|6 + g22 |∇
~ 2 φ|2 + ...... .
S = d d x φ? (−∇
2
4
Rescale :
Thors Hans Hansson (Stockholm University)
p~< →
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Dimensional analysis and flow equations
Mass dimensions: [g2 ] = 2 and [g4 ] = 4 − d (recall that [φ] =
under the scale transformation,
g2 → g20 = s 2 g2
and
d
2
− 1) so
g4 → g40 = s4−d g4
We expect g2 to be relevant and g4 relevant or irrelevant depending on
whether d < 4 or d > 4.
The RG equations are
s
dg
dgi
=
= βi (g1 , g2 , . . . )
ds
dt
The d = 4 β-functions can be obtained from perturbation theory,
dg2
= 2g2 + ag4
dt
dg4
= −bg42
dt
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
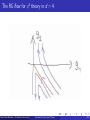
The RG flow for φ4 theory in d = 4
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Next subject
1
Fermi Liquids – Why, What, and How?
Why Fermi liquids?
What is a Fermi liquids?
Fermi Liquids – How?
2
Landau’s Phenomenological Approach
The free Fermi gas
Landaus basic idea
The Energy Functional E [n(p)]
The effective mass
The quasiparticle Fermi surface
When can Fermi Liquid theory be used?
Quasiparticle interactions
3
Renormalization Group approach to FL theory
An RG primer
Fermi Liquids as a RG fixed point
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Why fermions are different
For bosons the RG transformation restricts to momenta to a smaller and
smaller ball around p = 0 . An RG fixed point is a set of coupling
constants {gi }.
For fermions the momenta are restricted to a smaller ands smaller shell
around the Fermi momentum pF . An RG fixed point is a set of coupling
~
~
functions {fi (Ω)}
defined on the Fermi surface, p~ = pF Ω.
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Two body scattering
Consider scattering between two particles in d = 3 close to the Fermi
surface,
1+2→3+4
~ i , i = 1, . . . 4 where Ω
~ = (cos θ, sin θ).
Parametrize: ~ki = (pF + ki )Ω
~1 = Ω
~ 3 and Ω
~2 = Ω
~4
Ω
~1 = Ω
~ 4 and Ω
~2 = Ω
~3
Ω
~ 1 = −Ω
~ 2 and Ω
~ 3 = −Ω
~4
Ω
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
(I )
(II )
(III )
Quantum Field Theory for Condensed Matter
/ 39
Fixed point functions
A four particle interaction in momentum space can be written as,
Sint =
ˆ Y
4
i=1
dωi
X
ψp~†3 ψp~†4 ψp~2 ψp~1 f (ωi , ki , θi ) δ 2 (
X
p~i )δ(
i
~i
p
X
ωi )
i
Processes I and II are allowed for arbitrary angles θ1 and θ2 , and because
of rotational invariance, it is characterized by a fixed point function:
F (θ1 − θ2 ) = f (θ1 , θ2 , θ1 , θ2 ) = −f (θ1 , θ2 , θ2 , θ1 )
where the sign is due to fermi statistics.
The Process III is scattering between particles at opposite positions on the
Fermi circle. Here the coupling function can depend only on the angle
θ1 − θ3 ,
V (θ1 − θ3 ) = f (θ1 , −θ1 , θ3 , −θ3 ) .
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Flow equations
Here we just used geometric intuition to put in the constraints on the
angles ”by hand”, but a carful evaluation of the diagrams
taking the cutoff into account, will give the same result, and the flow eqs.
dF (θ)
=0
dt
ˆ
dV (θ)
1
dθ0
=−
V (θ − θ0 )V (θ0 )
dt
4π
2π
which has the solution:
VL (0)
VL (t) =
1 + VL (0)t/(4π)
where VL (0) are the starting values for the RG evolution.
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Physical interpretation
VL (t) =
VL (0)
1 + VL (0)t/(4π)
Take all VL (0) > 0, as would be the case for a reasonable repulsive
potential, then
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Physical interpretation
VL (t) =
VL (0)
1 + VL (0)t/(4π)
Take all VL (0) > 0, as would be the case for a reasonable repulsive
potential, then
V (θ) will renormalize to zero.
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Physical interpretation
VL (t) =
VL (0)
1 + VL (0)t/(4π)
Take all VL (0) > 0, as would be the case for a reasonable repulsive
potential, then
V (θ) will renormalize to zero.
F (θ) remains marginal and defines a fixed point theory which is a
Fermi liquid!!
If (at least) one VL (0) < 0 is , as would be the case for any attractive
interaction, the RG flow will hit a singularity for some t, and
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Physical interpretation
VL (t) =
VL (0)
1 + VL (0)t/(4π)
Take all VL (0) > 0, as would be the case for a reasonable repulsive
potential, then
V (θ) will renormalize to zero.
F (θ) remains marginal and defines a fixed point theory which is a
Fermi liquid!!
If (at least) one VL (0) < 0 is , as would be the case for any attractive
interaction, the RG flow will hit a singularity for some t, and
The coupling constant, VL grows out of control, and the perturbative
treatment can no longer be trusted.
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Physical interpretation
VL (t) =
VL (0)
1 + VL (0)t/(4π)
Take all VL (0) > 0, as would be the case for a reasonable repulsive
potential, then
V (θ) will renormalize to zero.
F (θ) remains marginal and defines a fixed point theory which is a
Fermi liquid!!
If (at least) one VL (0) < 0 is , as would be the case for any attractive
interaction, the RG flow will hit a singularity for some t, and
The coupling constant, VL grows out of control, and the perturbative
treatment can no longer be trusted.
The renormalization of V (θ) comes from the ”BCS” diagram c.
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39
Physical interpretation
VL (t) =
VL (0)
1 + VL (0)t/(4π)
Take all VL (0) > 0, as would be the case for a reasonable repulsive
potential, then
V (θ) will renormalize to zero.
F (θ) remains marginal and defines a fixed point theory which is a
Fermi liquid!!
If (at least) one VL (0) < 0 is , as would be the case for any attractive
interaction, the RG flow will hit a singularity for some t, and
The coupling constant, VL grows out of control, and the perturbative
treatment can no longer be trusted.
The renormalization of V (θ) comes from the ”BCS” diagram c.
Results in a pole in the Lth partial wave of the particle - particle
scattering amplitude, corresponding to the formation of a Cooper pair
with angular momentum L.
Thors Hans Hansson (Stockholm University)
Landau’s Fermi Liquid Theory
Quantum Field Theory for Condensed Matter
/ 39