Download Ionisation in a strong laser field

UNIWERSYTET JAGIELLOŃSKI
Instytut Fizyki Mariana Smoluchowskiego
Ionisation in a strong laser field
Jakub S. Prauzner-Bechcicki
PhD Thesis
supervised by
Professor Jakub Zakrzewski
Kraków, 2006
Oby mi Bóg dal slowo odpowiednie do myśli
i myślenie godne tego, co mi dano!
(Mdr 7, 15)
I would like to thank all the people that helped me to prepare this thesis.
First great thanks to Marysia and my family for all support and forbearance.
Thanks to Jakub Zakrzewski for giving me the opportunity to do my research and for support, Krzystof Sacha for the time that he spend with me
on discussions and for the help in advancing the numerical methods, Bruno
Eckhardt for his ideas that underlie the results presented here, fruitful discussions and hospitality in Marburg, Roman Marcinek for his patient hardware
and software support and the rest of the members of the Atomic Optics Department in the Institute of Physics at the Jaggielonian University for their
help.
Contents
1 Introduction
1.1 Description of the physical system . . . .
1.1.1 Atoms and molecules . . . . . . .
1.1.2 Interaction with external field . .
1.2 From single to multiphoton ionisation . .
1.3 Experiments on non-sequential ionisation
1.4 Theory of non-sequential ionisation . . .
1.5 Main goals . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2 Classical model
2.1 Ionisation of molecules within Eckhardt-Sacha approach .
2.2 Local analysis . . . . . . . . . . . . . . . . . . . . . . . .
2.2.1 Double ionisation . . . . . . . . . . . . . . . . . .
2.2.2 Triple ionisation . . . . . . . . . . . . . . . . . . .
2.3 Numerical simulations of double ionisation of molecules .
2.4 Towards quantum model . . . . . . . . . . . . . . . . . .
3 Quantum model
3.1 Physical Model . . . . .
3.2 Ionisation yield . . . . .
3.3 Momenta distributions .
3.4 Is it possible to measure
bution? . . . . . . . . .
. . . . . . .
. . . . . . .
. . . . . . .
interference
. . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . . . . . . . . . . . .
. . . . . . . . . . . . .
. . . . . . . . . . . . .
in the momenta distri. . . . . . . . . . . . .
.
.
.
.
.
.
.
3
4
4
5
8
10
13
19
.
.
.
.
.
.
21
22
25
28
31
37
44
47
. 48
. 50
. 59
. 70
Conclusions and outlook
75
A Numerical Methods
A.1 The Newton-Raphson method . . . . . .
A.2 Key ideas of the Bulirsch-Stoer algorithm
A.3 Operator Splitting . . . . . . . . . . . .
A.4 Forward Time Centred Space method . .
79
79
80
81
82
1
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2
CONTENTS
A.5 Evolution with use of the FFT algorithm . . . . . . . . . . . . 83
A.6 Smooth cutting and coherent adding . . . . . . . . . . . . . . 83
B List of Abbreviations
89
Bibliography
90
Chapter 1
Introduction
The invention of the laser in 1960 led to enormous progress in atomic and
molecular spectroscopy. Thanks to the laser, not only examination of properties of the matter is within reach of scientist, but also elucidation of fundamental properties of light-matter interactions becomes possible. Thus, at
the same time, the laser is a diagnostic instrument and its interaction with
the matter is of interests on its own right. Continuous developments in laser
techniques result in even broader range of possibilities, giving to the experimentalists more powerful tools. That in turn gives impact to progress in
theoretical description of observed phenomena.
For low laser intensities, laser-atom interaction can be treated within perturbation theory, but more and more sophisticated experiments enter region
of laser intensities in which perturbation theory fails. Huge laser intensities
are possible for pulsed lasers. Different pulse durations allow one to examine
phenomena occurring at different timescales. Further shortening of the pulse,
to the range of few femtoseconds [1, 2] or even to the range of hundreds of
attoseconds [3], leads to a situation in which the phase difference between
the carrier wave and the envelope of the pulse becomes important. All these
experimental possibilities urge theorists to develop new models and methods
to describe, explain and predict results of experiments. With use of various
numerical techniques accompanied with computers, constantly increasing in
their computing power, even nonperturbative regime becomes accessible.
Since the present dissertation is dedicated to theoretical description of
the ionisation of atoms and molecules in strong laser fields, supplied with numerical simulations, in the following chapter basic facts on atoms, molecules
and their interaction with electric field will be given. Moreover, as the nonsequential ionisation will be of special interest here, up to date experimental
results and theory of this phenomenon are shortly reviewed. And finally main
goals of the dissertation are pointed out and its structure is given.
3
4
Chapter 1. Introduction
Throughout this dissertation atomic units are used, unless noted otherwise. Atomic units are defined by setting m = h̄ = |e| = 4π0 = 1, that
gives:
• 1 atomic unit of energy = 4.3597×10−18 J = 27.2eV,
• 1 atomic unit of length = 0.5918×10−10 m,
• 1 atomic unit of time = 2.4189×10−17 s,
• 1 atomic unit of mass = 0.9109×10−30 kg,
• 1 atomic unit of momentum = 1.9928×10−24 kg·m·s−1 ,
• 1 atomic unit of electric field = 0.5142×1012 V·m−1 .
1.1
Description of the physical system
To describe a physical system and its evolution one may use its Hamiltonian, H. In general, in classical mechanics, the Hamiltonian is a function
of momenta, positions and time, H = H(p, q, t). Then one obtains from the
Hamiltonian a set of Hamilton’s equations which describe evolution of the
system, namely:
∂
ṗ = − ∂q
H(p, q, t)
(1.1)
∂
q̇ = ∂p H(p, q, t)
From these equations one obtains positions and momenta that describe the
state of the system. On the other hand, in quantum mechanics, the Hamiltonian is an operator composed of momenta and position operators, Ĥ =
Ĥ(p̂, q̂, t). And the state of the system is described by a wave function and
its non-relativistic evolution by the Schrödinger equation:
ĤΨ = i
∂
Ψ.
∂t
(1.2)
Thus, in the present section Hamiltonians of systems under consideration,
i.e. an atom or a molecule interacting with the laser field, will be presented.
1.1.1
Atoms and molecules
The most basic Hamiltonian considered here will be:
Ĥhyd
p̂2 1
=
− .
2
r
(1.3)
1.1 Description of the physical system
5
In classical mechanics, the Hamiltonian, eq. (1.3), describes the well known
Kepler’s problem [4] and here it describes the hydrogen atom. Coupling of
the atom or molecule to very strong laser field, as it will be considered here,
allows to neglect corrections to the internal structure such as isotope effect,
as well as, fine and hyperfine interaction effects.
Then an ”infinitely” heavy atom or ion of N electrons and charge number
Z, the Hamiltonian becomes:
N
X
X
p̂i 2 Z
1
Ĥat =
(
− )+
,
2
ri
|ri − rj |
i=1
i<j
(1.4)
and in general the problem described by such a Hamiltonian cannot be solved
exactly on both classical and quantum mechanical grounds.
For molecules the situation becomes even more complicated, because instead of single positive charge centre there are many (at least two) of such
centres. Keeping the assumption of infinitely heavy nuclei, the Hamiltonian
of the molecule composed of M nuclei and N electrons can be written as
follows:
N
M
X
X
p̂i 2 X
1
ZK
Ĥmol =
−
)+
,
(1.5)
(
2
|r
|r
i − RK |
i − rj |
i<j
i=1
K=1
where indices i and j are related to electrons and index K to nuclei, ZK is
charge of K th nucleus. The Hamiltonian, eq. (1.5), is the simplest model for
the molecule and the only difference between molecular species lies in the
number of nuclei and distances between them. Here the interaction with a
very short laser pulse will be considered, during such a short period of time
the molecule has not enough time to change its orientation [5, 6] and thus
the molecular degrees of freedom are frozen.
1.1.2
Interaction with external field
The atom exposed to the electromagnetic field of frequency that matches
the energy of an allowed transition will absorb or emit the electromagnetic
radiation, changing its internal state at the same time. If the field frequency is
high enough the atom can ionise. Moreover, the off-resonant electromagnetic
field also has an influence on the atom. Fields of small intensities induce
splittings and frequency-dependent shifts of energy levels. On the other hand,
in the off-resonant fields of high intensities multiphoton processes become of
importance. When the electromagnetic field is included the Hamiltonian of
6
Chapter 1. Introduction
the system becomes:
N
X
X
(p̂i + A(ri , t)/c)2
1
Z
(
Ĥ =
− Φ(ri , t) − ) +
,
2
r
|r
−
r
|
i
i
j
i=1
i<j
(1.6)
where Φ(r, t) is the scalar potential and A(r, t) is the vector potential, which
define the electric field F(r, t) and the magnetic filed B(r, t):
F(r, t) = −∇Φ(r, t) −
1 ∂A(r, t)
, B(r, t) = ∇ × A(r, t),
c ∂t
(1.7)
here c is the speed of light (c = 137 in atomic units).
For given electric and magnetic fields potentials are not unique and depend on the choice of the gauge. Under the gauge transformation, fields F
and B remain unchanged while potentials are replaced according to:
A → A + ∇Λ, Φ → Φ −
1 ∂Λ
,
c ∂t
(1.8)
where Λ is any scalar function of r and t.
For considerations presented in the dissertation the radiation gauge (the
velocity gauge) and the field gauge (the length gauge) are used. Taking a
laser pulse with the envelope shape given by function f (t) and the carrierenvelope phase, φ:
F(t) = Ff (t) cos(ωt + φ),
(1.9)
that is linearly polarised along z axis, i.e. F = (0, 0, F ), in the radiation
gauge potentials are:
Z t
Ff (t0 ) cos(ωt0 + φ)dt0 , Φ = 0,
(1.10)
A(t) = −c
0
and in the field gauge are:
A = 0, Φ(r, t) = −F · rf (t) cos(ωt + φ),
(1.11)
respectively.
The atom in a static field – the dc Stark effect As an example of
atom-field interaction an atom in a static, homogeneous electric field, F, will
be considered. In such a field atom experiences shift of its energy levels.
Assuming that the field is pointing in the z axis direction, the Hamiltonian
of the system reads:
Ĥ =
N
X
p̂i 2
i=1
2
+V +F
N
X
i=1
zi ,
(1.12)
1.1 Description of the physical system
7
Potential energy [a.u.]
where V is a potential describing the interaction of electrons with each other
and with nucleus. The energy shifts can be obtained by means of the perturbation theory treating last term in eq. (1.12) as a small perturbation [7, 8, 9].
However, such treatment is problematic, because the perturbing potential,
assuming that F is positive, tends to −∞ as the zi goes to −∞. The Hamiltonian, eq. (1.12), has no bound states and the states of unperturbed Hamiltonian, in the presence of the field, become resonances of width 1/τ , where τ
is the lifetime of the state with respect to the decay via field ionisation. The
more excited state of the unperturbed system is considered the shorter the
lifetime is. If the field is not too strong the low-lying states can be regarded
as bound [7].
In the classical picture the field ionisation is possible only if the considered
state has energy above the energy of the Stark saddle. For example, for the
hydrogen atom in the static positive electric field polarised in the z direction
the potential reads:
1
V (r) = − + F z,
(1.13)
r
√
and the saddle
is
located
on
the
negative
z-axis
at
z
=
−1/
F with energy
S
√
VS = −2 F (see Fig. 1.1).
1
0
-1
-10
0
z [a.u.]
10
Figure 1.1: Left panel: Potential energy, eq. (1.13), along z-axis for F = 0.1;
dashed line represents interaction part F z from the potential, eq. (1.13). Right
panel: Equipotential lines in the xz-plane; the Stark saddle is marked as the point
”S”.
This intuitive picture with the saddle in the potential created by presence of the field will be very helpful in understanding and describing the
8
Chapter 1. Introduction
phenomenon of the non-sequential ionisation in next chapters. Moreover,
basing on it a simplified quantum model of the non-sequential ionisation will
be proposed.
Problem of a multielectron atom or molecule interacting with the electromagnetic field cannot be solved exactly. Sometimes even perturbative
treatment is not the proper choice. Then one of the alternatives is the numerical approach. Classically the numerical treatment is relatively easy, i.e.
one has to solve a set of 6N first order differential equations, eq. (1.1). In
quantum mechanics, the numerical simulation of the corresponding system is
difficult, because of dimensionality of the Schrödinger equation, eq. (1.2), i.e.
a 3N dimensional partial differential equation. Therefore, various approximations have been proposed, just to mention the mean field approximation
or the reduction of dimensionality based on the symmetry of the considered
problem. Each of those approximation has its benefits and drawbacks, thus,
the choice of the method depends on the particular problem which is examined. This issue will be discussed later on and the description of numerical
methods used is presented in Appendix A
1.2
From single to multiphoton ionisation
Atom can be photo-ionised by absorbing a single photon from radiation whose
frequency matches or exceeds the ionisation energy of the atom. In first order
perturbation theory the photo-ionisation cross section is calculated by means
of Fermi’s Golden rule. For the single ionisation of the N -electron atom and
energy normalised radial wave functions of the outgoing electron the photoionisation cross section has the following form [7]:
4π 2
ω|ˆ
· dfi |2 .
(1.14)
c
Here ˆ is the polarisation vector of unit length and dfi is the matrix element
of the electric dipole operator between initial and final states. To obtain the
photo-ionisation cross section, eq. (1.14), the following approximations are
involved: the dipole approximation (DA), i.e. A(r, t) ≈ A(t), and a single
active electron model (SAE). The DA works in a case of laser wavelengths
much larger than the size of the atom and for λ 100Å is well justified. In
SAE model it is assumed that interaction of the ionised electron with the rest
of electrons can be included as an effective potential (like in Hartree-Fock
methods), i.e. only one electron is allowed to absorb energy and ionise, while
the other electrons remain effectively frozen at the core [10, 11, 12, 13, 14].
One can further generalise single photo-ionisation to multiphoton ionisation, which follows from absorption of several photons at the same time.
σph (E) =
1.2 From single to multiphoton ionisation
9
Multiphoton transitions were first considered theoretically, just to mention
that two-photon transitions were studied theoretically by Goeppert-Mayer
already in 1930’s [15]. Their experimental observation needed, however, a
source of intense radiation due to small two-photon cross section and appeared just in 1950’s [16, 17, 18]. Later on, together with the invention of
the laser, not only multiphoton transition between bound states were possible to study, but also multiphoton ionisation (MPI) became accessible and
was observed in 1960’s [19, 20, 21, 22, 23].
In order to describe theoretically the multiphoton transitions one has to
apply perturbation theory up to the very high order. On the other hand, most
crucial element of the experimental set-up, if one wishes to observe MPI, is
a very intense radiation source. However, the increase in the intensity of
the source leads to regime in which perturbation theory is not appropriate
for description of the observed phenomena. To characterise different possible regimes one has to consider three distinct energy scales: the energy of
the light quantum (ω), the ionisation potential (Ip ) and the ponderomotive
energy (Up ) [24]. The ponderomotive energy is related to the stimulated scattering of photons on free electrons in the intense laser field and classically
manifests as the force on the electron driven by the E and B fields in the
light beam [25, 26]. This wiggle energy scales as the intensity of the light,
I = F 2 , and inversely with the square of the frequency, namely [24, 27, 28]:
F2
Up =
.
4ω 2
(1.15)
The ’ponderomotive force’ acts along the gradient of the beam intensity, is
independent of the light polarisation and in most instances is equal to the
spatial derivative of the ponderomotive energy, eq. (1.15), i.e. −∇Up . In
this sense, the ponderomotive energy may be regarded as a potential energy,
although, it is a kinetic energy in its origin [24, 25].
Thus, MPI happens in the following regimes:
1. Ip > ω Up - in this regime multiple-order perturbation theory may
by used;
2. Ip > Up > ω - in this regime the above-threshold ionisation (ATI) 1 and
the high-order harmonics generation (HHG) 2 appear and perturbative
treatment is not appropriate;
1
ATI is a phenomenon when a number of absorbed photons is much larger than the
minimum number required to reach the ionisation threshold [29]
2
HHG is creation of very high, odd harmonics of the laser radiation through coherent
excitation and deexcitation of highly energetic continuum states [30]
10
Chapter 1. Introduction
3. Up > Ip ω - in this regime suppressed barrier ionisation appears 3 .
Processes considered in presented dissertation are observed in the second and
third of above listed regimes, thus the perturbative treatment is not used.
For MPI the generalised n-photon cross section is not linear with laser
intensity [24, 27, 28]:
Γ = σn I n .
(1.16)
Such a non-linear intensity dependence of the ionisation rate was observed
experimentally for quite low intensities [31, 32, 33]. Another effect observed
quite early was a depletion of atoms form the enlightened volume due to
ionisation. Thus, there exists a saturation intensity, Is , above which number
of ions changes more slowly than expected from eq. (1.16) [31, 32, 33].
The next step in the consideration of MPI is quite natural and concerns
multiple ionisation of multi-electron atoms or molecules, i.e. the removal of
several electrons and production of multiply charged ions. Here experiments
revealed a new phenomenon, the non-sequential ionisation (NSI), i.e. simultaneous ionisation of two or more electrons [33, 34, 35]. Single ionisation of
atoms or molecules, likewise ATI or HHG can be described within the SAE
model. Such an approximation in the case of multiple ionisation and laser
intensities below the saturation value gives ionisation rates that are much
smaller than experimentally observed [33, 36, 37, 38, 39]. That is so, because in SAE model, electrons leave the atom sequentially, i.e. first single
ion is created, then double ion, triple and so on. Thus, the experimental
data suggest that the interaction between electrons is an important feature
and has to be included correctly in the theoretical description. This and
later experimental observations of collective behaviour of electrons triggered
vivid theoretical discussion on the origins of the process. The present thesis
is aimed on the theoretical description of NSI of atoms and molecules within
classical, as well as, quantum mechanics supported with numerical simulations. Therefore in the next two sections present status of experimental and
theoretical knowledge on NSI will be reviewed in more detailed way.
1.3
Experiments on non-sequential ionisation
In the early experiments [31, 32, 33] a linearly polarised laser pulse was focused into a vacuum chamber filled with noble gas vapour. The ions produced
by interaction of atoms with the laser pulse were extracted from the focal
volume through application of a transverse electric field and separated by a
3
It also includes the static field ionisation - compare to dc-Stark effect in Sec. 1.1.2
1.3 Experiments on non-sequential ionisation
11
time-of-flight spectrometer and then detected in an electron multiplier. Experiments were performed with 1.064 µm and 0.53 µm laser wavelenghts in
a wide range of laser intensities (1013 − 1014 Wcm−2 ) for Xe, Kr, Ar, Ne and
He atoms and showed, especially in case of Xe, that the double ionisation
rates for intensities below the saturation intensity, Is , were larger than those
predicted basing on SAE models [31, 32, 33] (see the left panel in Fig. 1.2).
From those results it was concluded that the direct double ionisation dominates over a stepwise process for intensities below the saturation intensity,
although mechanism of such direct process was not established. Further
experiments with different polarisations of the laser pulse showed that the
direct double ionisation is suppressed in a circular polarisation [34, 40]. Along
with those experiments there appeared different models of the process, just
to mention the re-scattering [38, 41] or the shake-off [35] scenarios (more
detailed discussion on theoretical models is presented in the next section).
It has been realised that the non-sequential multiple ionisation manifests experimentally as a ”knee structure” in the ionisation yield curve (see
Fig. 1.2). That structure exposes and emphasises the underestimation of the
multiple ionisation probability calculated from SAE models.
In the late 1990’s similar experiments were performed also for small
molecules, such as the N2 and the O2 . In the case of the N2 , the direct double ionisation manifested itself through the presence of ”knee” in the double
ionisation yield but no such a structure was observed for the O2 [42, 43, 44].
That result led to the debate on the influence of the molecular structure on
the process of the non-sequential double ionisation of molecules. This issue
will be here addressed on the grounds of classical mechanics.
A new type of experiments in which a pre-cooled supersonic gas jet was
used along with a technique of cold target recoil ion momentum spectroscopy
(COLTRIMS; see review articles [45, 46]) brought a fresh insight into the
non-sequential double ionisation reporting the correlated emission of electrons [47, 48, 49, 50]. In those experiments momenta of the ion and one of the
electrons were measured and the momentum of the second electron has been
extracted via the momentum conservation law, i.e. pion ≈ −(pe1 + pe2 ) - the
photon momentum is negligible on the scale of interest4 . The most astonishing result obtained in those experiments was the distribution of the electrons’
momentum components measured along the polarisation of the laser pulse
which showed that electrons predominantly escaped with equal momenta (see
the left panel in Fig. 1.3) [47]. That fact was visible in the recoil-ion momentum distribution for doubly charged ions as a ”double hump” structure (see
the right panel in Fig. 1.3) [48]. This observation, besides the ”knee struc4
Photons energy of 1.5 eV≈0.55 a.u. corresponds to a momentum of only 0.0004 a.u.
12
Chapter 1. Introduction
Figure 1.2: Left panel: Experimental yields measured in [31], best fit (solid lines)
and calculated yields for Xe+ and Xe2+ ions at 1.06 µm (dashed lines). Curve
B corresponds to the direct double ionisation from the atom and curve C relates
to sequential ionisation. Saturation intensity is 1.2×10 13 Wcm−2 . Figure taken
from [31]. Right panel: Ion yields for He for the linearly polarised, 100 fs, 780 nm
laser pulse. Solid lines represent calculations based on SAE model. Figure taken
from [34].
ture”, became key features used in testing and justifying different theoretical
models of NSI.
Recent experiments reported also electron momentum correlation in the
case of diatomic molecules [5, 51], however, once again the molecular case
appeared to be much more complicated than the atomic one. The experiment showed differences between molecular species, namely in the case of
N2 it seemed that electrons escape with similar momenta along field polarisation axis more often than in the case of O2 [5]. Moreover, owning to the
fact that diatomic molecules can be differently oriented with respect to the
polarisation axis it was shown that the orientation of the molecule affects a
double non-sequential process as well [51]. Those aspects of non-sequential
double ionisation of molecules would be addressed in the present dissertation
basing on a classical model of the phenomena.
The latest development in laser techniques allowed to use ultra-short laser
pulses (up to 7 fs at 795 nm wavelength [1] and 5 fs at 760 nm [2]) in mul-
1.4 Theory of non-sequential ionisation
13
Figure 1.3: Left panel:Momentum correlation of outgoing electrons in the Ar
atom double non-sequential ionisation for a 800 nm laser pulse of 220 fs duration at peak intensity 3.8×1014 Wcm−2 . Axes correspond to components of the
electrons’ momenta measured in the direction of laser polarisation. Figure taken
from [47]. Right panel: Distribution of He 2+ ion momenta in the direction of the
polarisation. The peak intensities are - (a) 2.9×10 14 Wcm−2, (b) 3.8×1014 Wcm−2
and (c) 6.6×1014 Wcm−2. Figure taken from [48].
tiple ionisation experiments. That enables suppression of processes occurring on time scales longer than one laser cycle, for example the sequential
ionisation, and in a consequence leads to much more detailed experimental
study of NSI [1]. Furthermore, experiments with a fixed carrier-envelope
phase revealed the dependence of momentum distribution of ions produced
in the non-sequential double ionisation on that phase [2]. Such situation
gives another great opportunity to test various theoretical models of the nonsequential ionisation phenomena, stimulates its deeper analysis and provides
better understanding.
1.4
Theory of non-sequential ionisation
Along with the detailed experimental investigation [34, 40, 35] theoretical explanations of observed phenomena were proposed, such as the rescattering [38, 41] or the shake-off [35], but still problem was not settled.
14
Chapter 1. Introduction
Models based on either of these scenarios using different mathematical tools,
e.g. S-matrix theory [52, 53] or a numerical solution of a simplified Schrödinger
equation [54, 55], were able to reproduce the ”knee structure” in the double
ionisation yield but until publication of the joint momenta distribution [47] it
was difficult to judge which scenario is the correct one. Experiments with the
circular polarisation showed drop in the double ionisation yields in regions
below the saturation intensity [34, 40] favouring the re-scattering scenario.
But it was the momentum distribution showing the correlation of outgoing
electrons that gave theorists a powerful argument in the debate on the mechanism of NSI, finally showing disagreement with the shake-off proposal and
strengthening position of the re-scattering scenario.
The shake-off mechanism was proposed together with the first experimental, well pronounced observation of the non-sequential ionisation in He [35].
This scenario assumes that for intensities high enough first electron ionises,
either by tunnelling or over-the-barrier escape, so quickly that the second
electron cannot adiabatically fit to the ground state of He+ , which is tightly
bound, and most probably is left in excited state of He+ , which is then
immediately ionised. For low intensities at laser wavelenghts used in the experiment (λ=614 nm) the first electron escapes so slowly that the state of
the second electron can adiabatically adjust to the ground state in the new
potential for which coupling to the continuum states at these photon energies is negligible [35]. Thus, the model suggests existence of threshold value
for intensity, below which the shake-off is not possible, but such a threshold
was not observed experimentally. As mentioned before, the main argument
against the shake-off mechanism was given by the experimental results on the
momenta correlation [47, 48]. It follows from a simple classical reasoning. If
the electron escape was governed by the shake-off process both electrons
would be freed near the field extremum. That would mean that near the
field extremum a doubly charged ion is created with zero initial velocity.
That in turn would result in an ion momenta distribution with maximum at
the zero momentum, what is in contradiction with experimental results [48].
Final ion momenta as a function of the release time are shown in Fig. 1.4.
Solid line corresponds to the pulse shape for the laser at frequency ω=0.0742
a.u. and maximum field amplitude value of F =0.2 a.u. 5 . The Gaussian
shape of the pulse was assumed and for the sake of clarity only 4 field cycles
are considered, that results roughly in an 8 fs pulse. Circles are showing the
final momentum of the ion as a function of a ”birth” time. As can be easily
noticed, ions created near field extrema end up with momenta around the
5
According to the laser parameters used in experiment, i.e. λ=614 nm and intensity,
I=1.5×1014 Wcm−2 , respectively [35].
15
1.4 Theory of non-sequential ionisation
20
0,2
10
0,1
0
0
-0,1
-10
-20
0
Field
Momentum
100
200
300
Field Amplitude [a.u.]
Final momentum [a.u.]
zero value. If they were not created close to the field extremum, they could
gain some momenta in the end. However, this classical picture can be misleading at the same time, because it would suggest that doubly charged ions
are created when the laser field is zero. As it shall be explained later on it is
not the case, i.e. the presence of the high field amplitude is necessary in the
appearance of doubly charged ions. Nevertheless, the shake-off mechanism
is not capable in reproducing momenta distributions and therefore gives in
to the re-scattering scheme.
-0,2
Time [a.u.]
Figure 1.4: Final ion momenta (circles) as function of the release time for the
pulse parameters as in Fittinghoff et. al experiment [35] (see in text). Black line
corresponds to the pulse shape.
In the re-scattering scenario the multiphoton ionisation is regarded as a
three step process [36, 37]. The model originates from the plasma physics
and is based on an observation that the multiphoton ionisation does not
instantaneously lead to a well-separated ion and electron, but rather, within
next optical cycles, there is a significant probability of finding the electron
in vicinity of the nucleus [41]. Therefore it is assumed that at the beginning,
one electron tunnels out through the Stark saddle and then it is returned
back to the nucleus [41, 56]. This is the first step and it happens within a
half cycle, i.e. the half cycle is the shortest period of time needed for the
electron to return to the nucleus. In the second step, in the act of scattering
16
Chapter 1. Introduction
- as the electron returns to its parent ion the act of scattering is called
’re-scattering’ - the returning electron brings back to its parent ion some
energy, as it is accelerated by the field, and shares this energy with the other
electron. Finally, in the third step, both electrons escape.
Agreement of the re-scattering model with experimental results [34, 40]
can be inferred by the analysis of the first step. Here reasoning of Corkum [41]
will be followed, namely, the probability of the ionisation of the first electron,
P (t), during given time interval, dt is given by:
P (t) = w(F (t))dt,
(1.17)
where w(F (t)) is the ionisation rate determined basing on Ammosov-DeloneKrainov (ADK) theory of the tunnel ionisation [57]:
w(F (t)) = Ip |Cn? l? |2 Glm (2
(2Ip )3/2 2n? −m−1
2(2Ip )3/2
)
exp(−
),
|F (t)|
3|F (t)|
(1.18)
?
here
p Ip is the ionisation potential of an atom under consideration, n =
IH /Ip with IH as the ionisation potential of hydrogen, l and m are orbital and magnetic quantum numbers, respectively, l ? is the effective quantum number given by l? = 0 for l n or l? = n? − 1 otherwise, and
?
finally |Cn? l? |2 = 22n [n? Γ(n? + l? + 1)Γ(n? − l? )]−1 and Glm = (2l + 1)(l +
|m|)!(2−|m| )/|m|!(l − |m|)!. F (t) is the electric field:
F (t) = F (cos(ωt)ex + α sin(ωt)ey ),
(1.19)
where a parameter α is responsible for polarisation of the field, α = 0 describes the linearly polarised light and α = ±1 the circular polarisation. The
tunnelling model suggests that the wave packet of the escaping electron is
created with the biggest efficiency near each field extremum (see the left
panel in Fig. 1.5).
Thereafter evolution of the electron in the laser field is considered to be
classical and independent of the interaction with the ion, this defines the so
called simple man model [41, 56]. The electron motion in the field is governed
by solutions of Newtonian equations of motion, i.e.:
x
y
vx
vy
=
=
=
=
−x0 cos(ωt) + v0x t + x0x ,
−αx0 sin(ωt) + αv0y t + y0y ,
v0 sin(ωt) + v0x ,
−αv0 cos(ωt) + v0y ,
(1.20)
where v0 = F/ω, x0 = F/ω 2 , and v0x , v0y , x0x and y0y are initial conditions
derived from position and velocity of an electron at the time of tunnelling.
17
1.4 Theory of non-sequential ionisation
0,2
150
-1
0,1
2
100
1.5
0
1
Field [a.u.]
x [a.u.]
Ionization rate [ 10
-5
0,1
50
0
0
-50
Field [a.u.]
s ]
2.5
-0,1
0.5
0
0
-0,1
0,2
0,4
0,6
Time in field cycles
0,8
1
-100
-150
0
0,5
1
1,5
-0,2
2
Time in field cycles
Figure 1.5: Left panel: The ionisation rate (dashed line) as a function of time
calculated basing on ADK model [57]. Right panel: Trajectories of an electron
for different single ionisation times - t 1 < 0.5 field cycles (dashed-dotted lines),
t2 = 0.5 field cycles (dotted line) and t 3 > 0.5 field cycles (dashed lines) for the
linearly polarised light; the horizontal dashed line indicates a position of the ion.
Both panels: the black solid line represents the laser field for ω = 0.06 a.u. and
F = 0.119 a.u..
Corkum claims that it is justified by comparison with an experiment that
the initial position and velocity can be assumed to be zero at the time of
ionisation [41]. While it may be true for the velocity, it is not for the initial
position. From the fact that the electron tunnels out through the Stark saddle follows that it has to appear at the bigger distance from the nucleus than
the distance at which the saddle is present. Thus, the initial position should
be estimated with respect to the position of the saddle and, in this sense,
with respect to the laser intensity (see Sec. 1.1.2). Moreover, neglecting the
electron-ion interaction is an oversimplification that leads to an underestimation of the ionisation yields [58]. Nevertheless, the simple man model, as
simple as it is, is able to describe the non-sequential ionisation qualitatively
giving a lot of insights into understanding the process. It should be stressed
that for a very strong field the simple man model gives similar results to the
one obtained with the Coulomb interaction included. After all, eqs. (1.20)
illustrate the fact that for the circular polarisation the electron never returns
to the neighbourhood of the nucleus. Therefore there is no possibility to
acquire enough energy to free two electrons at once. The second electron can
only by ionised later on, sequentially, that leads in short pulse experiments
to noticeable fall off in the double ionisation yield in the region below the
saturation intensity [34, 40].
Moreover, from eqs. (1.17), (1.18) and (1.20) it is easily seen, that only
18
Chapter 1. Introduction
some of the electrons that have been field ionised near a given field extremum
will revisit the parent ion (dotted and dashed lines in the right panel in
Fig. 1.5 are exemplary trajectories for such electrons). The others will never
return to the vicinity of the nucleus (dashed-dotted lines in the right panel
in Fig. 1.5 are exemplary trajectories for such electrons). And furthermore,
from eqs. (1.17), (1.18) and (1.20) it follows that maximal velocity of the
electron passing the nucleus matches the energy E = 3.17Up , where Up is the
ponderomotive potential, eq. (1.15), i.e. in a single re-scattering event the
electron cannot bring more energy than E = 3.17Up (see Fig. 1.6) [41].
4
3.17Up
Energy/ Up
3
2
1
0
0,5
0,6
0,7
0,8
0,9
1
Release time in field cycles
Figure 1.6: Energy as a function of an electron release time. The cut-off energy
of 3.17Up is indicated by an arrow.
There is a lot of questions that arise from this simple description, even
though it allows to reproduce experimental results. Those questions which
will be addressed, to some extent, in the present dissertation are quoted. One
of the problems is the controversy on the moment of return of the electron,
whether it hits its parent ion when the field is zero, as suggested by a simple
classical picture, or when the field is decelerating the electron, so called ’slowdown collisions’ [59], or when the field is still pushing it towards the ion. In
aforementioned simple picture the importance of the carrier-envelope phase
for a very short laser pulse was omitted completely as the field was assumed
to be just cosine. From this point another question arises, namely whether
the non-sequential double ionisation is phase dependent. If so, then it could
be used as an instrument to measure the carrier-envelope phase [2, 60]. And
1.5 Main goals
19
another one, that has already been pointed out along with the presentation
of experimental results (see Sec. 1.3), how NSI depends on the molecular
species. A physical situation with so many open question is very stimulating
both for experimentalists and theorists.
As a last one, the collective multielectron tunnelling was investigated as
a possible mechanism responsible for NSI and, after all, it has been shown
that the total ionisation rate calculated within this scenario is far too small
to match experimentally observed ones [61]. Thus, finally agreement that
the re-scattering is the correct model for the non-sequential ionisation was
established in the community and therefore it is assumed in every calculations
presented in the following.
1.5
Main goals
The present thesis aims on the theoretical description of the non-sequential
ionisation. As stated in preceding sections, 1.3 and 1.4, there are still many
open questions concerning the phenomenon and some of them will be addressed here. Both the classical and the quantum approach will be presented.
Therefore, for the sake of clarity, main goals of the present dissertation are
summarised and divided into two groups:
• The classical analysis of NSI for simple two-atomic homo-nuclear molecules
will aim on:
– Understanding of the discrepancy in the non-sequential double
ionisation for different molecular species.
– Analysis of the dependence of the momenta distribution on the
molecule orientation with respect to the polarisation axis.
– The local analysis of channels for the triple ionisation of molecules.
• The quantum mechanical description of the non-sequential double ionisation (NSDI) of atoms will include:
– Reproduction of all key features of NSDI of atoms, i.e the knee
structure in the ionisation yield, the double hump structure in the
ion’s momentum distribution and the electrons momenta distribution showing the signatures of the correlated escape.
– Analysis of the carrier-envelope phase dependence of NSDI.
– Preliminary analysis of the quantum interference in NSDI.
20
Chapter 1. Introduction
The classical analysis of NSI for molecules is contained in the second
chapter, where also first remarks that lead to a simplified quantum description are given. In next, third chapter the quantum model for the double
ionisation in a strong laser field is described. That description is followed
by the detailed analysis of the quantum model that results in obtaining the
ionisation yields and momenta distributions. Moreover quantum analysis reveals new directions of research, namely the possibility of observing quantum
interference. The last chapter is a conclusion and outlook for further studies.
For the sake of completeness short discussion of the numerical methods used
is presented in Appendix A and the list of abbreviations used throughout the
dissertation is given in Appendix B.
Chapter 2
Classical model
The re-scattering scenario is well-established as a description of the mechanism governing NSI. In order to get all the information about the whole
process one should solve the relevant Schrödinger equation governing the
evolution of, at least, a two electron atom in a time dependent electric field.
That is a formidable task due to the dimensionality of the problem. There
have been made some attempts to treat this problem in a full space, but
mostly for the wavelength smaller than used in the experiment [62, 63, 64].
Recently, with the use of advanced multiprocessor parallel computing methods first 3D calculations for the experimental wavelength of 780nm have
been performed [65]. Nevertheless, other than full 3D approaches are of a
interest in order to make some theoretical predictions within a reasonable
time interval and with the use of more easily commercially available machines, rather than very advanced supercomputers. To this end, one can use
different theoretical tools together with some approximations based on the
symmetry of the problem or other types of physical assumptions. One of
such simplifications was already presented in Sec. 1.4, where the evolution
after the tunnelling of the first electron was described by Newtonian equations of motion in which the interaction with the nucleus was neglected. In
the following chapter, another simplified treatment is proposed, namely a
classical model of a highly excited diatomic molecule interacting with the
intense laser field will be examined.
Considerations presented in this chapter are much in the spirit of the
classical analysis developed by Bruno Eckhardt and Krzysztof Sacha [66,
67, 68, 69, 70]. Their approach is adapted to the molecular case [71, 72].
Moreover, on the basis of observations made by Eckhardt and Sacha in [66,
68, 73] with the use of this classical picture a simplified quantum model for
the non-sequential double ionisation of atoms is proposed that will be used
in further research. In this sense classical analysis becomes a starting point
21
22
Chapter 2. Classical model
for later quantum mechanical study.
First, physical grounds underlying the Eckhardt-Sacha approach are summarised and precise forms of the molecular Hamiltonians used later on are
presented. Then, the results of the local analysis of the potential are discussed and followed by a presentation of the effects of numerical simulations.
The classical description ends up with the sketch of the quantum model, that
will be a starting point for the next chapter. The part of the present chapter
concerning the double ionisation of molecules is based on the data published
in articles [71, 72], and results on the triple ionisation that are not published
yet.
2.1
Ionisation of molecules within EckhardtSacha approach
In the following the physical grounds underlying the Eckhardt-Sacha approach are described and the use of this approach to the case of molecules
is presented. As it has been mentioned in Sec. 1.4 the whole process of the
multiple direct ionisation, can be considered as a three step process: a single
ionisation and the electron’s return, a re-scattering event and a double or
multiple ionisation [36, 37]. Consider, for simplicity, the double ionisation
of atoms. Eckhardt and Sacha in [66, 68] argued that during a very violent
event of the collision a highly excited state of two electrons is created. The
re-scattering takes place close to the core, where interactions are very strong
and the electron dynamics is fast and non-integrable, thus all the details of
the previous electron motion are lost. Moreover, the compound state that
is created during the collision is a short lived, highly unstable complex. It
decays quickly in different ways through a single, double ionisation or another re-scattering, after which the whole process may repeat. In this sense,
the highly unstable complex separates the re-scattering event, in which the
energy transfer takes place, from the final ionisation, that can be identified
as a single or double. Thus, the final features of the double non-sequential
ionisation, such as the double hump structure in the ion momenta distribution, should mostly depend on the decay of the highly excited compound
[66, 68]. The analysis proposed by Eckhardt and Sacha [66, 67, 68, 69, 70]
is similar to the one used by Wannier in the case of a double ionisation upon
an electron impact [74, 75, 76, 77], nevertheless it will be referred to as the
Eckhardt-Sacha approach.
Therefore, the Eckhardt-Sacha classical approach describes the decay of
the highly excited state of the atom or molecule. The first two steps of the
23
2.1 Ionisation of molecules. . .
re-scattering scenario are included as initial conditions, through the fact that
re-scattered electron brings certain amount of energy creating the highly excited state. Moreover, both those steps are assumed to happen in the same
way for all kinds of atoms and molecules (more elaborated comment on this
assumption is made later on at the end of classical analysis in Sec. 2.3 on
pg. 41). Such a highly excited compound state can be described by the
Coulomb interaction between electrons and nuclei only. Then, what is considered is the evolution of electrons in combined Coulomb and external fields.
The whole classical calculations consist of two parts. In the first part the
main objective is to identify the channels of decay that lead to the double
or higher ionisation. This goal is achieved by means of the local analysis of
the potential with use of the adiabatic approximation. The adiabatic approximation follows from the fact that the classical motion of the electrons
in a highly excited compound state is fast compared to the field oscillations.
Moreover, the strong interaction of the electrons with the nuclei and with
each other ’erases’ memory of the previous motion, so that the initial state
for the multiple ionisation is a statistical distribution of electrons close to the
nuclei [66, 68]. The second part is based on numerical simulations of the classical motion of two or more electrons in a combined Coulomb and laser field,
which allow to study signatures of identified channels in the distribution of
electrons’ and ion’s momenta. In the case of molecules, dependencies of the
properties of identified channels and momenta distributions on the molecular
species and the molecular orientation with respect to the polarisation axis
are examined.
The Hamiltonian of the two-atomic homo-nuclear molecule that will undergo the double or single ionisation will have the form of eq. (1.5) and the
interaction with the linearly polarised laser field is described in the length
gauge, eq. (1.11):
H=
X p̂2
1
( i + Vi + zi F f (t) cos(ωt + φ)) +
,
2
|r1 − r2 |
i=1,2
(2.1)
here Vi is the Coulomb interaction of i-th electron with both nuclei, F is the
field amplitude, ω is the field frequency and φ is the carrier-envelope phase.
The pulse envelope, f (t), is assumed to have following form:
f (t) = sin2 (πt/Td ),
(2.2)
where Td is the pulse duration:
Td = n
2π
,
ω
(2.3)
24
Chapter 2. Classical model
and n is the number of cycles in the pulse.
For the matter of convenience, the origin of coordinate system is placed
in the centre of mass of the nuclei. Then two parameters appear explicitly,
namely: d, the distance between nuclei, and θ, the angle between the molecular axis and the z axis (the polarisation axis). Without loss of generality it
is assumed that the molecule lies in the xz plane and therefore the potential
energy for each electron becomes:
1
Vi = − q
(xi + d2 sin θ)2 + yi2 + (zi + d2 cos θ)2
1
.
−q
d
d
2
2
2
(xi − 2 sin θ) + yi + (zi − 2 cos θ)
(2.4)
Note, that in fact a hydrogen-like molecule with a different internuclear
spacing, d, will be under consideration. Here distances d =2.067 a.u. and
d =2.28 a.u. will be recognised as N2 and O2 molecules, respectively. The
motion of the molecular core is frozen owing to the fact that during short laser
pulse molecule has not enough time to change its orientation[5, 6]. However,
the dependence of the non-sequential double ionisation on an orientation of
the molecule will be also examined within this simplified description, as in
the experiment molecules differently oriented with respect to the polarisation
axis contribute to the final results.
Later on in the numerical simulations to avoid divergences in the integration of the equations of motion, a smoothing factor e in the Coulomb
potentials between the electrons and nuclei, Eq. (2.4), [78, 79], is introduced.
Then the potential terms read
1
Vi = − q
(xi + d2 sin θ)2 + yi2 + (zi + d2 cos θ)2 + e
1
−q
.
(xi − d2 sin θ)2 + yi2 + (zi − d2 cos θ)2 + e
(2.5)
The smoothing factor e = 0.01 is chosen. This value introduces negligible
influence on the evolution and the local analysis in interesting regions.
For the triple ionisation the Hamiltonian, eq. (2.1), slightly changes, i.e.
the summation goes up to 3, two additional terms in the electron-electron
interaction part appear (namely the interaction between 1st and 3rd , as well
as, between 2nd and 3rd electron) and the potential energy of each of the
electrons is changed, while one of the nuclei is assumed to have a double
positive charge.
2.2 Local analysis
25
At this point, it should be stressed that sometimes all the multiple ionisation events that happen after the re-scattering process are referred to as
being non-sequential. The classical analysis, as evidenced in [66], clearly
suggests to distinguish events in the double ionisation where both electrons
escape during the same half-cycle of the electric field after the formation
of the highly excited state and those where there is a time-delay of one or
several half-cycles. The latter are undoubtedly sequential. However, even
during the same half-cycle both sequential and non-sequential processes may
happen. The sequential path involves a single ion as a mid point, it means
then that when the second electron escapes the first one is rather far away
from it. Large distance between electrons means a weak mutual interaction
between them. On the other hand, if electrons leave the atom or molecule
simultaneously the distance between them is rather small, meaning that their
mutual interaction is strong. Such a picture suggests to call ’non-sequential’
those events that happen in the same half-cycle and in which the interaction
between electrons is crucial. Thus, in the following the term ’non-sequential’
will be used only in that meaning, exclusively.
2.2
Local analysis
In this section the results of the local analysis of the double and the triple
non-sequential ionisation of diatomic homo-nuclear molecules are shown. For
one electron in the Coulomb potential, a superimposed external field opens
a Stark saddle over which the electron can ionise (see Sec. 1.1.2). In case of
two electrons, if there were no interaction between them, they could escape
simultaneously through the same saddle on top of each other. But when
the repulsion between electrons is taken into account, the Stark saddle for
the simultaneous electron escape splits into two saddles that lie on opposite
sides of the field polarisation axis [66, 67, 68]. For atoms the two saddles
lie symmetrically with respect to the polarisation axis and the motion of the
electrons can be analysed in some symmetry subspace [68, 69]. For diatomic
molecules, such as N2 or O2 , that will not be the case since the molecules
possess their own symmetry axis which can be oriented at an arbitrary angle
with respect to the polarisation axis, thus destroying the global rotational
symmetry. Nevertheless, an external field will introduce saddles over which
electrons can escape. The aim, then, is to identify those saddles and to this
end the local analysis of the potential will be applied.
Consider the potential V (q) being a function of coordinates q = (q1 , ..., qn ).
First, in order to find the saddle points one has to solve, in general, the non-
26
Chapter 2. Classical model
linear set of equations:






∂V (q)
∂q1
∂V (q)
∂q2
=0
=0
.
..

.



 ∂V (q) = 0
∂qn
(2.6)
The set of equations (2.6) gives only positions of extremal points (stationary points) and one has to check, whether a given point is a minimum, a
maximum or a saddle point. Moreover, in many cases the only possibility
to solve (2.6) is by means of numerical methods, here the Newton-Raphson
method is used (see Appendix A.1).
Once, the extremal points are found, the next step is to expand the
potential around a given fixed point, qS , in the Taylor series, that is:
1 X ∂2V
(
V (q) = V (qS ) +
)|q (qi − qSi )(qj − qSj ) + . . . .
2 i,j ∂qi ∂qj S
(2.7)
Of course the linear terms vanish due to (2.6). An approximation of the
potential by the second order terms leads to a harmonic analysis and gives
the possibility to determine neutral, stable and unstable directions in the
phase space. Unstable directions correspond to the ionisation: single, double
or multiple. In order to determine those directions the Jacobi matrix,
Aij = (
∂2V
)q ,
∂qi ∂qj S
(2.8)
has to be diagonalised. Neutral direction is defined by an eigenvalue equal
to zero. Stable directions are defined by eigenvectors corresponding to positive eigenvalues and unstable by those corresponding to negative eigenvalues,
respectively.
The local stability analysis of the saddles reveals neutral, stable and unstable directions. In the case considered here, one unstable direction corresponds to the ’reaction coordinate’ for the double (or triple) ionisation,
i.e. the symmetrical escape. The other unstable direction reflect interactions
that will push electrons away from the double (triple) ionisation path; if successful, they will push one (or two) electron back to the molecular core. If
only one electron escapes the remaining one will typically be in a highly excited state and will have a chance to singly ionise during another field-cycle.
But following the distinction introduced earlier, such an event would not be
called non-sequential.
The cross section behaviour close to the classical threshold for the simultaneous electron escape can be obtained from the Lyapunov exponents that
27
2.2 Local analysis
characterise the different unstable directions. As in the case of the double ionisation without a field, analysed many years ago by Wannier [74, 75, 76, 77],
the competition between various unstable directions gives rise to an algebraic
variation of the cross section with energy close to the threshold, namely,
σ(E) ∝ (E − VS )α ,
(2.9)
where VS is the saddle energy and the cross section exponent contains the
Lyapunov exponents,
P
λi
α= i ;
(2.10)
λr
λr is the Lyapunov exponent of the unstable direction corresponding to the
non-sequential double ionisation path, and λi are the Lyapunov exponents
of all other unstable directions of the saddle [80, 67]. Similarly, the cross
section exponent is calculated in the case of the triple ionisation. Then, λr is
the Lyapunov exponent of the unstable direction corresponding to the nonsequential triple ionisation path and λi are the Lyapunov exponents of all
other unstable directions of the saddle.
The method described above is used to analyse the potential of the two
electron and three electron diatomic molecule in the presence of the laser field.
Here some short comment on the nomenclature has to be made. Solving the
set of equations (2.6) for the potential of a diatomic molecule, one finds
stationary points in the six-dimensional space and in this sense one identifies
saddles in this 6D space. And thereafter one identifies stable and unstable
directions in this 6D space. However, the experiment takes place in the
3D space and this 6D picture has to be mapped to a 3D picture. Namely,
one saddle in the 6D space corresponds to a pair of Stark saddles in the
3D configuration space. Or more precisely, the saddle in 6D corresponds
to a pair or a triple of points (or more points - it depends on the number
of electrons that is considered) in the 3D configuration space that identify
positions of electrons on the saddle. If there were no interaction between
electrons then the electrons would have the same position on the saddle in
the 3D space having its counterpart in 6D, as was mentioned before. As it
will be shown later on, for the general orientation of the molecule there will
be more then one saddle in 6D and each saddle will correspond to a pair of
points in 3D for the double ionisation or to a triple of points for the triple
ionisation. Therefore, for the sake of clarity and simplicity, the saddles in
the 6D space will be called simply the saddles. Each point from the group
of points indicating positions of the electrons in 3D for a given saddle from
the 6D space will be called the Stark saddle, respectively. Then, each saddle
in 6D will have as its counterpart a group of Stark saddles in 3D.
28
2.2.1
Chapter 2. Classical model
Double ionisation
Consider first the double ionisation. Since the diatomic molecule possesses
its own symmetry axis, two distinct situations have to be analysed. Namely,
one with the molecule aligned (θ = 0) and the other with the molecule tilted
(θ 6= 0) with respect to the polarisation axis. For the molecule oriented along
the field axis the problem possesses the axial symmetry. Solution of the
set (2.6) indicate existence of a single saddle point. Diagonalising the Jacobi
matrix, eq. (2.8), one neutral, two unstable and three stable directions for
such an orientation are found. The neutral direction is connected with overall
rotation around the field axis. One of the unstable directions corresponds
to the symmetric escape of the electrons and the other to the situation,
when one electron escapes and the other is turned back to the nuclei. The
corresponding Stark saddles are placed symmetrically with respect to the zaxis and due to the axial symmetry they form a ring of Stark saddles around
the field axis in the full configuration space (vide the neutral direction).
Switching to the cylindrical coordinates (ρi , ϕi , zi for i−th electron) one
can easily define a symmetry subspace of the electron motion. Restricting
the electrons to a plane (i.e. ϕ1 − ϕ2 = π) their coordinates in the C2v
symmetry subspace are ρ1 = ρ2 = R, z1 = z2 = Z and the potential energy
reduces to
2
V = − q
R2 + (Z − d2 )2
(2.11)
1
2
+ 2F (t)Z.
+
−q
2|R|
d 2
2
R + (Z + 2 )
As an example of a tilted molecule consider first the case of the perpendicular orientation. The solution of the set (2.6) reveals existence of two
saddle points and diagonalising the Jacobi matrix, eq. (2.8), shows that each
of them possesses the same number of unstable directions, namely two. Both
unstable directions have the same interpretation as in the case of an aligned
molecule: one corresponds to a symmetrical escape of two electrons along the
z axis and the other to a single ionisation of one of the electrons and the turn
back of the other. One of the saddles corresponds to the pair of Stark saddles
in xz plane, the other to the pair in the yz plane. Therefore, for the molecule
oriented perpendicularly to the field there are two C2v symmetry subspaces.
One subspace is defined in the xz plane, the other in the yz plane. In the
former case, the electron coordinates in the subspace are x1 = X, y1 = 0,
29
2.2 Local analysis - Double ionisation
z1 = Z and x2 = −X, y2 = 0, z2 = Z and the potential energy reads
2
V = − q
(X − d2 )2 + Z 2
(2.12)
1
2
+ 2F (t)Z.
−q
+
(X + d2 )2 + Z 2 2|X|
For saddles which are in the yz plane coordinates are x1 = 0, y1 = Y , z1 = Z
and x2 = 0, y2 = −Y , z2 = Z and the potential energy is
V = − q
4
d2
4
+
+ Y 2 + Z2
1
+ 2F (t)Z.
2|Y |
(2.13)
The potential functions, eqs. (2.11), (2.12) and (2.13), are shown in Fig. 2.1
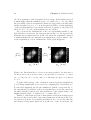
for a set of parameters corresponding to the nitrogen molecule with an internuclear distance of d = 2.067 a.u. and for the field F = 0.07 a.u.. The
saddles are clearly visible.
6
5
5
4
X
R
Y
0
0
2
–5
0
–5
0
Z
5
–5
–5
0
Z
5
–5
0
5
Z
Figure 2.1: Section through equipotential surfaces of the adiabatic potential,
V = V1 + V2 + V12 + VF , for fixed time t and for two symmetric orientation of
the molecule, namely parallel (θ = 0, left panel corresponding to Eq. (2.11)) and
perpendicular to the field polarisation axis, Z, (θ = π/2, middle and right panels
corresponding to Eq. (2.12) and Eq. (2.13), respectively); the molecular parameter
d = 2.067 a.u. and the external field F (t) = −0.07 a.u.
The case of a general orientation of the molecule is similar to the one with
a perpendicular orientation: there are two pairs of Stark saddles for the nonsequential ionisation, one in the plane defined by the molecular axis and the
field, and the other outside this plane. These two channels become equivalent
when the molecule is parallel to the field axis and the axial symmetry is
restored.
30
Chapter 2. Classical model
The properties of the saddles depend on the internuclear distance, d, as
shown in Fig. 2.2. Starting with d = 0 (in which case the orientation angle
θ is meaningless since a molecule reduces to an atom) and increasing d the
energy VS of the saddle corresponding to the parallel orientation (θ = 0)
is always the lowest and it decreases. For the other extremal orientation,
i.e. θ = π/2, the energies of the saddles (there are two saddles because
of the axial symmetry breaking) increase and their values are the highest.
Analysing the dependence of cross section exponent, α, on the internuclear
distance we see that for increasing d the cross section exponent of one of the
saddles (corresponding to θ = π/2) goes up while the other goes down. The
exponent for θ = 0 increases only slightly.
-1.18
θ=0
θ=π/2
θ=π/2
1.6
θ=0
θ=π/2
θ=π/2
1.5
-1.2
α
VS [a.u]
-1.19
-1.21
1.4
-1.22
1.3
-1.23
0
0.5
1
1.5
d [a.u.]
2
2.5
1.2
0
0.5
1
1.5
d [a.u.]
2
2.5
Figure 2.2: Energy of the saddle (left panel) and cross section exponent (right
panel) as a function of internuclear distance, d, for orientations of the molecule
parallel and perpendicular to the field axis, θ = 0 and θ = π/2, respectively. The
dashed line corresponds to the saddle in the xz-plane and the dash-dotted line to
the saddle in the yz-plane. The external field is F (t) = −0.07 a.u.
Variations of the parameters of the saddles with the orientation angle,
θ, are shown in Fig. 2.3 for the internuclear distances corresponding to the
nitrogen, N2 , with d = 2.067 a.u., and the oxygen, O2 , with d = 2.28 a.u.
The energy VS of all saddles increases and the exponent α of one member of
the saddle pairs increases while the other decreases. Fig. 2.3 shows that the
energies and exponents for the N2 and O2 molecules are quite similar — the
largest differences between the species are of the order of few percent. Taking
into account that the experimental results [5, 6] are for a statistical mixtures
of different molecular orientations, it may concluded that from the point of
view of local analysis of the non-sequential decay channels one should not
expect differences between the N2 and the O2 . Moreover, the local analysis
shows that the NSDI should not depend on the orientation either. However,
31
2.2 Local analysis - Triple ionisation
both conclusions, the lack of dependence on the molecular species and the
independence of orientation are in contradiction to experimental results [5, 6,
51]. That fact suggests that differences observed in experiments have origin
in processes that lead to creation of the highly excited compound state, i.e.
the tunnelling and the re-scattering. This observation is also discussed later
on along with the analysis of results of numerical simulations (see pg.41).
N2
O2
1.6
N2
O2
1.5
-1.2
α
VS [a.u.]
-1.19
-1.21
1.4
-1.22
1.3
-1.23
0
0.1
0.2
0.3
θ [π]
0.4
0.5
0
0.1
0.2
0.3
θ [π]
0.4
0.5
Figure 2.3: Energy of the saddle (left panel) and cross section exponent (right
panel) as a function of orientation angle, θ, for N 2 (d = 2.067 a.u.) and 02 (d = 2.28
a.u.) molecules. For both molecules the top line corresponds to the saddle in the
yz-plane, whereas the bottom line corresponds to the saddle in the xz-plane. The
external field is F (t) = −0.07 a.u.
2.2.2
Triple ionisation
In order to analyse the channels leading to a triple ionisation of the molecule
within the Eckhardt-Sacha approach one has to use a slightly different potential function, namely:
V =
3
X
i=1
(Vi + zi F (t)) +
1
1
1
+
+
,
|r1 − r2 | |r2 − r3 | |r1 − r3 |
(2.14)
where the Coulomb potentials ,Vi , describe the interaction of i − th electron
with the nuclei:
1
Vi = − q
(xi + d2 sin θ)2 + yi2 + (zi + d2 cos θ)2
2
,
−q
(xi − d2 sin θ)2 + yi2 + (zi − d2 cos θ)2
(2.15)
32
Chapter 2. Classical model
and F (t) is kept constant according to the adiabatic assumption, see Sec 2.1.
Those slight differences have an effect on the symmetry of the problem,
namely, the positive charge centres, that represent nuclei, are no longer symmetric. That asymmetry in the nuclear charge with respect to the centre of
mass should be taken into account in the analysis.
First, two possible alignment with respect to the polarisation axis are
examined, namely θ = 0 and θ = π. They differ in the position of a stronger
positive charge with respect to the slope induced by the field. Nevertheless,
both cases possess an axial symmetry. Solution of the set (2.6) indicate
existence of two saddle points for each of the orientations. Those saddles
slightly differ in the energy, i.e. for F = 0.07 a.u. and θ = 0 saddle’s
energies are VS = −2.11 a.u. and VS = −2.04 a.u., whereas for the same
field and θ = π they are VS = −1.97 a.u. and VS = −1.9 a.u. The energy
difference between different alignments is a consequence of the asymmetry in
the positive charge. It can be understood with the use of following argument:
the field is F = 0.07 a.u. and for θ = 0 the negative part of the slope
introduced by the field (i.e. where the part of the potential F (z1 + z2 + z3 )
is negative) which opens the saddle is closer to the bigger charge and such
configuration lowers the energy of the saddle. In the case of θ = π situation
reverses and the smaller charge is closer to the negative slope, that in turn
lifts the energy up.
On the other hand, for both parallel alignments of the molecule the saddles have the same geometry in the 3D, i.e.
x
x
d
d
z
y
z
Figure 2.4: Configuration of the two saddles for triple non-sequential ionisation.
Left panel: the triangular configuration. Right panel: In-plane configuration. On
both panels big circles mark the positions of the nuclei and small ones positions of
the Stark saddles, arrows indicate unstable direction responsible for simultaneous
escape, d is the internuclear distance.
2.2 Local analysis - Triple ionisation
33
• the saddle with the lower energy transforms in the full configuration
space into Stark saddles that are at the vertexes of an equilateral triangle in a plane perpendicular to the polarisation axis (see the left panel
in Fig. 2.4); the position of the plane in which the triangle lies depends
on the position of the stronger charge with respect to the slope induced
by the field, that is for θ = 0 the plane lies a bit further from the centre
of the coordinate system than for θ = π — this configuration will be
called triangular;
• the saddle with the higher energy transforms into Stark saddles that
are at the vertexes of an isosceles triangle in a plane parallel to the
field axis (in fact the plane contains field axis, see the right panel in
Fig. 2.4 ), the triangle is oriented in such a way that its base is closer
to the nuclei and its two vertexes lie symmetrically with respect to the
polarisation axis, the last vertex lies on the polarisation axis; and again
for θ = 0 all three Stark saddles are at larger distance from the centre
than it is for θ = π — this configuration will be referred to as in-plane.
Owing to the fact that both alignments have an axial symmetry in the full
configuration space there is a whole family of saddles with low energy which
configuration is the equilateral triangle and all of them, in fact, lie on the
ring around the field axis. On the other hand, the saddle with the higher
energy in the configuration space is in fact a whole family of saddles with
the in-plane configuration. That family of saddles lies on a cone, whose apex
lies on the polarisation axis and is identified with the Stark saddle that lies
on the axis, the remaining two Stark saddles lie on the ring of the base of
the cone. Both saddles have the same configuration as in the case of triple
non-sequential ionisation of the atoms [69].
Diagonalising the Jacobi matrix, eq. (2.8), different number of unstable
and stable directions for each of the saddles is found. For both alignments the
saddle with the lower energy (the triangular configuration) has three unstable directions, five stable ones and one neutral direction, whereas the saddle
with the higher energy (the in-plane configuration) has four unstable directions, four stable ones and one neutral direction. For both configurations
the neutral direction corresponds to an overall rotation around the field axis
(vide the ring and the cone). In the triangular configuration one of the unstable directions corresponds to the symmetric escape of the electrons. The
second unstable direction corresponds to the situation, when one electron
escapes and the other two are turned back to the nuclei or reversal of it, i.e.
it corresponds to a single or a double ionisation. The last one describes the
situation when one electron escapes, the second is turned back, closer to the
nuclei and the third would not change its position much, thus it is also single
34
Chapter 2. Classical model
-1,9
-1,9
Triangle configuration
In-plane configuration
-1,95
VS [a.u.]
VS [a.u.]
-1,95
-2
-2,02
-2,05
-2
-2,05
-2,03
-2,1
0
-2,04
0,2
0,4
-2,1
0,4
0,42
0,6
θ[π]
0,44
0,8
1
0
θ=0
θ = π/2
θ=π
0,5
1
1,5
2
2,5
d [a.u.]
Figure 2.5: The energy of saddles for the triple non-sequential ionisation as a
function of the orientation angle for the N 2 , d = 2.067 a.u., (left panel) and as a
function of the distance between nuclei (right panel) - here upper lines correspond
to the in-plane configuration and bottom lines to the triangle configuration. Both
panels are for the field amplitude F = 0.07 a.u.
ionisation event. Unstable directions identified for the in-plane configuration correspond to similar situations. One unstable direction for the triple
symmetric escape in the plane in which the Stark saddles lie, one for both
double and single ionisation and one for the single ionisation only. The fourth
unstable direction corresponds to deviations along the y axis: two electrons
are moving in the plane perpendicular to the polarisation axis in the same
direction, say positive values of y, the third electron moves in the opposite
direction, i.e. towards negative y, and in another plane perpendicular to the
polarisation axis. Nevertheless, in the case of each configuration there is one
reaction coordinate, i.e. the unstable direction responsible for the simultaneous triple escape, all other unstable directions will compete with it. In
the case of atoms each of this configurations lead to different ion momenta
distributions and thus being available to the experimental distinction [69].
Consider different orientations of the molecule, i.e. θ 6= 0, π. In such
situation the axial symmetry is broken and thus there will not be the ring for
the triangular nor the cone for the in-plane configurations. However, the ring
splits into two possible triangular configurations that are differently located.
They are no longer in the plane perpendicular to the field axis, but in planes
with some angle to it. Moreover, those triangles become isosceles. One of
these triangles has the base closer to the nucleus with the higher charge, the
other is located with the base closer to the nucleus with the lower charge.
Those changes are due to the asymmetry in the charge of the nuclei, and
35
2.2 Local analysis - Triple ionisation
both triangles cannot be mapped to each other simply by the use of rotation.
Those configurations are almost equal in the energy (see the inset in the left
panel in Fig. 2.5) and have the same number of unstable directions as the
ring of the triangular, namely three. The unstable directions have the same
interpretation as in the case of aligned molecule.
3,8
θ=0
θ = π/2
θ=π
α
α
2,65
θ=0
θ = π/2
θ =π
3,7
3,716
3,712
2,6
0
1,6
3,6
0,5
1
1,5
d [a. u.]
2
2,5
0
0,5
1
1,5
2
1,8
2
2,5
2,2
3
d [a. u.]
Figure 2.6: The cross section exponent as a function of the distance between
nuclei for the triangle configuration (left panel) and the in-plane configuration
(right panel) for the field amplitude F = 0.07 a.u.
The cone of the in-plane configuration splits into two distinct in-plane
configurations, which lay in different planes. Namely, one lies in the xzplane, but is no longer in a form of a isosceles triangle. It is in a form of a
triangle with different sides. This configuration has the lower saddle energy
(see the left panel in Fig. 2.5). The other in-plane configuration lies in the
plane almost parallel to the yz-plane and has a bit higher energy (see the left
panel in Fig. 2.5), but remains isosceles. However, diagonalising the Jacobi
matrix, eq. (2.8), reveals the same number of unstable directions as for the
cone of the in-plane configuration for each of those configurations, namely
four. Those unstable directions have the same interpretation as in the case
of the aligned molecule.
Potential functions for both the N2 and the O2 molecules possess the
same number of saddles with the same number of unstable directions and
the same configuration. The change of the energy of saddles with increasing
internuclear distance is presented in the right panel in Fig. 2.5. The bigger
distance between nuclei the more distinct becomes the pair of saddles into
which split the cone of the in-plane configurations. On the other hand, the
energy difference between saddles into which splits the ring of the triangle
configurations does not change much as the distance between nuclei grows
36
Chapter 2. Classical model
and both triangle configurations have almost equal energy (see the right
panel in Fig. 2.5). Also the cross section exponent does not change much
with increasing internuclear distance (see Fig. 2.6). However, for the triangle
configuration for both alignments the cross section exponent increases as the
distance between nuclei grows, whereas for the tilted molecule it decreases
(see left panel in Fig. 2.6). On the other hand, for the in-plane configuration
cross section exponents for both alignments almost do not change (see right
panel in Fig. 2.6), whereas for tilted molecule each of the in-plane configurations into which the cone of the in-plane configuration has split behaves
differently. Namely, for the in-plane configuration that lies in the xz plane
the cross section exponent decreases, while for the in-plane configuration that
lies in the yz plane increases (see right panel 2.6).
4
3,5
Triangle
In-plane
α
2,64
2,63
2,62
3
2,5
0
2,61
2,6
0,2
0,4
0,2
0,6
0,4
0,6
θ [π]
0,8
1
Figure 2.7: The cross section exponent as a function of the orientation of the
molecule with respect to the polarisation axis; the triangle configuration (solid
line) and the in-plane configuration (dashed line) for the field amplitude F = 0.07
a.u.
As for atoms [69], the triangle configuration has always smaller cross section exponent, than the in-plane configuration (see Figs. 2.6 and 2.7). That
suggest that the triangle configuration is the dominant one. Different triangle configurations that appear when the molecule is not aligned with respect
to the polarisation axis do not differ much among themselves, the same is
2.3 Numerical simulations. . .
37
in the case of the in-plane configurations (see Fig. 2.7). Similarly like in
the double ionisation case, it seems that there should not be dependence on
the orientation of the molecule for the triple ionisation, at least from the
point of the local analysis. Changes in the energy of the saddles and in cross
section exponents are too small to favour one angle (see Fig. 2.7). Moreover, the differences in properties of saddles for different molecular species
do not suggest dominance of any of them. Once again it is stressed, that all
conclusions drawn from the local analysis refer only to the final stage of the
non-sequential process and assume that previous stages, that lead to creation
of the highly excited compound state, proceed in the same way for different
molecules or different molecular orientations. As has been shown in the case
of double ionisation, the local analysis compared with experimental results
suggests dependence of the tunnelling or the re-scattering events on both the
orientation or species of the molecule. Thus, one should rather expect the
same in the case of the triple ionisation.
2.3
Numerical simulations of double ionisation of molecules
So far the local analysis of the potential within the adiabatic assumption has
been discussed. Now results of the numerical simulations of the dynamics of
the double ionisation process in the time-dependent laser field (i.e. adiabatic
assumption is not used) will be presented. To this end, the set of Hamilton’s
equations, eq. (1.1), derived from the Hamiltonian describing movement of
two electrons in combined Coulomb and laser fields, eqs. (2.1) and (2.5), is
solved with the use of the Bulirsch-Stoer algorithm (see Appendix A.2).
During the final stages of the re-scattering event both electrons are highly
excited and they pass close to the nuclei where they interact strongly with
them and with each other. Therefore, it is reasonable to assume, as mentioned in Sec. 2.1, that all the memory of the earlier motion is lost. Then the
initial state of the final stage for the double ionisation is a statistical distribution of two electrons close to the nuclei. Hence, initial values of positions
and momenta with respect to the micro-canonical distribution for a given
initial energy E are chosen. The energy should be in the range between −I
and −I + 3.17Up , where I is the ionisation potential of the second electron
(the first electron is considered to be ionised [41, 81]). However, since for the
non-zero field the system is open, it is difficult to define the micro-canonical
distribution of initial conditions. Even for the energy of the complex chosen
properly and for a fixed time. Thus an additional constraint that zi = 0 is
38
Chapter 2. Classical model
used. It has the advantage that the dipole moment along the field is zero and
thus the electron-field interaction drops out from the Hamiltonian, eq. (2.1)
(initial conditions do not depend on the initial field phase). Moreover, results are not sensitive to a particular choice of the confinement [68]. Then
positions may be chosen
p micro-canonically, but (for convenience) with one
more constraint that x2i + yi2 < 85 a.u.. There is a small chance to find the
electrons at a lager distance from the nuclei with an energy from the considered range, excluding situations in which one of the electrons is already
ionised of course. In all simulations an ensemble of 105 trajectories is used
and the laser frequency is set to be ω = 0.057 a.u., that corresponds to the
laser wavelength λ = 795 nm.
(a) (a)
2
150
100
0
50
−2
(b)
2
250
200
0
150
100
−2
50
0
−2
0
0
2
(c)
2
−2
30
25
20
0
15
10
−2
5
0
2
(d)
2
120
100
80
0
60
40
−2
20
0
−2
0
2
0
−2
0
2
Figure 2.8: Final distribution of electrons’ momenta parallel to the field axis for
different initial energy, E and different pulse length (i.e. number of cycles in the
pulse, n) in the double ionisation of the nitrogen molecule parallel to the field axis.
The field strengths is F = 0.07 a.u., the frequency ω = 0.057 a.u., the internuclear
distance d = 2.067 a.u. and the orientation parallel to the field, θ = 0. The plots
differ in initial energy E and the number of field cycles n: (a) E = −0.3 a.u.,
n = 2; (b) E = −0.3 a.u., n = 26; (c) E = −0.6 a.u., n = 2 and (d) E = −0.6
a.u., n = 26.
To simulate a real experiment one should consider a distribution of different initial energies of the complex and also different moments in a pulse when
the complex is created. However, within the Eckhardt-Sacha approach a fully
39
2.3 Numerical simulations. . .
(a)
(b)
counts/bin
0.3
counts/bin
0.3
0.2
0.2
0.1
0
0.1
-4
-2
0
p || [a.u.]
2
4
0
-4
-2
0
p || [a.u.]
2
4
Figure 2.9: Final distribution of the ion’s momentum parallel to the field axis
corresponding to Fig. 2.8. F = 0.07 a.u., ω = 0.057 a.u., d = 2.067 a.u. and θ = 0.
(a) E = −0.3 a.u., n = 2 - solid line and n = 26 - broken line; (b) E = −0.6 a.u.,
n = 2 - solid line and n = 26 - broken line.
quantitative description of the ionisation process is not possible. Thus the
analysis is restricted to a inspection how the final distributions of electrons’
momenta change with a change of the initial energy, the pulse duration, the
molecule species or the orientation. All simulation are started at the peak
of the pulse — starting at different moments changes the range but not the
structure of the distributions [68, 69].
Distributions of the final electrons’ momenta parallel to the field axis for
different initial energies, E, and for different pulse durations are presented
in Fig. 2.8. All the data in the figure correspond to the N2 molecule oriented
along the field axis. For very short laser pulses (n = 2 cycles) signatures of
the simultaneous electron escape are clearly visible — the distributions are
localised along the diagonals indicating that the electrons escape predominately by passing close to the saddles analysed in Sec. 2.2. For longer pulses
the distributions change their character. The first and fourth quadrants of
the panels become strongly populated implying that a number of sequential
decays significantly increases. The reason for that is quite obvious. After the
re-scattering when a highly excited two electron complex is created, both the
non-sequential double escape and the single ionisation are possible. During
the next cycles, singly ionised molecule can emit their second electron, thus
also contributing to the double ionisation. As the pulse becomes longer, the
number of such sequential ionisation events increases, even to the point of
overwhelming the number of direct, non-sequential double ionisation events.
Thus for sufficiently long pulses, even though the re-scattering scenario is
involved in the double ionisation process, the momentum distributions will
40
Chapter 2. Classical model
also show signatures of the sequential electron escape. If the initial energy E
is much higher than the minimal energy of a saddle (VS ≈ −1.2 a.u.) then
the probability of the non-sequential ionisation is bigger and even if the pulse
duration is quite long (e.g. n = 26 in the panel (b) in Fig. 2.8) the signatures
of the non-sequential process remain noticeable (contrary to the panel (d)
where for E = −0.6 a.u. such signatures are not visible).
Fig. 2.9 shows the distributions of the ion’s momentum parallel to the
field axis that correspond to the data presented in Fig. 2.8. As expected, the
distributions are much narrower in the case when the sequential ionisation
dominates than in the case when the non-sequential processes dominate. Also
as the sequential process is dominant the double peak disappears.
(a)
2
120
100
pz2
0
[a.u.]
80
60
40
−2
20
(b)
2
60
50
p z2
0
[a.u.]
40
30
20
−2
10
0
0
−2
0
2
pz1 [a.u.]
−2
0
2
pz1 [a.u.]
Figure 2.10: Final distribution of electrons’ momenta parallel to the field axis for
the nitrogen molecule at non-zero angle to the field axis. F = 0.07 a.u., ω = 0.057
a.u., d = 2.067 a.u., E = −0.3 a.u. and n = 2. The angles are (a) θ = π/4 and (b)
θ = π/2
Together with a change of the orientation of the molecule the distributions
do not change significantly as one can see by comparing Fig. 2.10 and Fig. 2.8.
For the field amplitude used in the simulations (which corresponds also to
the experiment [5]) saddles for the non-sequential process are far away from
the nuclei and the positions and other parameters of the saddles change only
slightly with the angle of orientation θ — compare Fig. 2.3.
Finally, to address the problem of discrepancies between molecular species
the data for the O2 molecule for the same parameters are shown in Fig. 2.11.
As expected, from the local analysis presented in Sec. 2.2, for the same initial energies E and pulse durations as in the case of the N2 molecule, the
41
2.3 Numerical simulations. . .
(a)
2
160
140
(b)
2
300
250
120
200
pz2
0
[a.u.]
100
80
60
p z2
0
[a.u.]
150
100
40
−2
20
−2
50
0
−2
0
2
pz1 [a.u.]
0
−2
0
2
pz1 [a.u.]
Figure 2.11: Final distribution of electrons’ momenta parallel to the field axis for
the oxygen molecule parallel to the field axis for different pulse length. F = 0.07
a.u., ω = 0.057 a.u., d = 2.28 a.u., E = −0.3 a.u. and θ = 0. (a) n = 2 and (b)
n = 26.
observed momentum distributions are very similar, compare Fig. 2.8. In the
experiment of Eremina et al., [5] the results for the O2 differ considerably
from those for the N2 . The latter shows signatures of the simultaneous electron escape while for the O2 it seems that the sequential process dominates.
The present analysis indicates that there is practically no difference between
the N2 and the O2 if similar initial conditions for the highly excited complex
are used. It thus strongly suggests that the differences between the observations for the two molecules are due to differences in the early stages of
the excitation process and the nature of the compound state before the final
decay towards multiple ionisation. This deduction is also supported by the
fact that from the local analysis of the double and the triple ionisation follows that there are neither qualitative nor significant quantitative differences
between the N2 and the O2 molecules.
Such a conclusion agrees well with results of Muth-Böm et al. [82] and
Grasbon et al. [83], whose analysis indicate that the symmetry of the valence
orbital (N2 has σg , the bonding symmetry and O2 has πg , the anti-bonding
symmetry) has an influence on the above-threshold ionisation spectra. Thus
it may affect also the excitation process and, in particular, the initial conditions for the decay of the highly exited complex for different molecular
species. That, in turn, may modify the final parallel momenta distributions.
42
Chapter 2. Classical model
For the sake of completeness, the case of the oxygen molecule is analysed
also for another set of parameters, as it is the molecule which does not
reveal simultaneous escape of electrons in experiment. The laser intensity
and the pulse duration are relatively easily controllable experimentally and
as explained before, at least, the pulse duration may have a big impact on the
momenta distribution. Therefore the oxygen molecule is now exposed to the
laser pulse of a slightly larger amplitude and two different pulse durations.
The larger field amplitude indicates the larger energy range, as it changes
the ponderomotive potential (see eq.( 1.15)), which sets the upper limit on
accessible energies.
700
2
700
2
600
600
500
0
400
300
500
0
400
300
200
−2
100
200
−2
100
0
0
−2 0
2
!"
−2 0
2
# 8
2
7
0
5
50
2
6
40
4
3
0
30
20
2
−2
1
−2
10
0
0
−2 0
2
−2 0
2
Figure 2.12: Final distribution of electrons’ momenta parallel to the field axis
for different initial energy, E and different pulse length (i.e. number of cycles in
the pulse, n) in the double ionisation of the O 2 molecule. The field strength is
F = 0.075 a.u., the frequency ω = 0.057 a.u., the internuclear distance d = 2.28
a.u. and the orientation parallel to the field, θ = 0. The plots differ in initial energy
E and the number of field cycles n: (a) E = −0.05 a.u., n = 2; (b) E = −0.05 a.u.,
n = 26; (c) E = −0.9 a.u., n = 2 and (d) E = −0.9 a.u., n = 26.
In Fig. 2.12 distributions of the final electrons’ momenta parallel to the
field axis for the O2 molecule oriented along the field axis and in Fig. 2.13
43
2.3 Numerical simulations. . .
the momentum distributions for molecule oriented at a non-zero angle with
respect to the field axis are presented. For high energies of the compound
state, E = −0.05 a.u., the correlated escape is even more pronounced than it
was in the nitrogen case, see Fig. 2.8. That is due to the fact, that such energy is much higher than the minimal energy of the saddle (VS ≈ −1.27 a.u.).
What is more, the concentration along the diagonal does not change significantly even for a longer pulse (compare panels (a) and (b) in Fig. 2.12).
For longer pulses and for the smaller energy, E = −0.9 a.u., (the panel (d)
in Fig. 2.12) the distribution drastically changes its character similarly as it
happened for the N2 (compare the panel (d) in Fig. 2.8). Namely, as a number of sequential decays significantly increases the first and fourth quadrants
of the panel become strongly populated. And finally, as in the case of the N2
the momentum distribution does not change much as the orientation of the
molecule alters (see Fig. 2.13).
(a)
(b)
11
600
10
2
2
500
9
8
7
400
p z2 0
300
[a.u.]
200
p z2 0
6
5
[a.u.]
4
3
−2
100
−2
2
1
0
−2
0
2
p z1
[a.u.]
0
−2
0
2
p z1
[a.u.]
Figure 2.13: Final distribution of electrons’ momenta parallel to the field axis for
the O2 molecule at non-zero angle to the field axis, i.e. θ = π/4, and for different
initial energy E. F = 0.075 a.u., ω = 0.057 a.u., d = 2.28 a.u. and n = 2. The
energies are (a) E = −0.05 a.u. and (b) E = −0.9 a.u.
Comparing the data for both molecules it may be concluded that a high
initial energy leads to much clearer signatures of the simultaneous electron
escape (even for long pulses) than a low energy. The initial energy is determined in the re-scattering process, thus to enhance signatures of the simultaneous escape one should apply a stronger external field. Increasing the field
amplitude is, however, dangerous because for very strong laser pulses the sequential ionisation (with and without the re-scattering) becomes dominant.
The compromise can be reached by an increase of the amplitude with simul-
44
Chapter 2. Classical model
taneous reduction of the pulse duration — very short laser pulses and the
field stronger than that used in Ref. [5] should allow for a clear observation
of the simultaneous electron escape in the double ionisation, even for the O2
molecules.
The presented results together with the local analysis of the double and
the triple ionisation from a previous section suggest that from the point of the
final stage of the non-sequential ionisation, i.e. decay of the highly excited
complex, the nitrogen and the oxygen molecules do not differ, in the sense
that both of them can show signatures of the simultaneous double escape.
What is more, the orientation of the molecule with respect to the polarisation
axis does not influence significantly the final momentum distribution for the
initial energy range considered. Furthermore, the analysis also indicates
that very short and stronger laser pulses should increase the ratio of the
non-sequential to the sequential ionisation. It opens a possibility for an
observation of clear signatures of the simultaneous electron escape both for
the N2 and the O2 molecules, but in particular for the oxygen, where the
sequential events seem to dominate the non-sequential ones.
2.4
Towards quantum model
As has been noted before, a full quantum mechanical calculation of two electrons interacting with the nucleus and with the external laser field becomes
possible only with the use of very advanced computers and mostly for parameters that are not necessarily realistic [62, 63, 64, 65]. Therefore, simplified
approaches that will be able to reproduce, at least qualitatively, main features
of the process that is examined and give a deeper insight into it are of a great
interest. One of the possible ways to achieve this goal is to reduce the dimensionality of the problem basing on the symmetry that the problem possesses.
The classical analysis proposed by Eckhardt and Sacha [66, 67, 68, 69, 70],
as well as, the one presented in previous sections suggests one of such possible simplifications. Namely, electrons in order to escape simultaneously in a
correlated manner have to pass sufficiently close to the saddle responsible for
the symmetrical escape. What is more, in the case of atoms Stark saddles
in 3D, that correspond to the saddle for the non-sequential double ionisation
in 6D, lie symmetrically with respect to the polarisation axis. As the field
changes they move along the lines that keep a constant angle with respect to
this axis (see Fig. 2.14). From that fact follows the idea to constrain the electrons motion to 1D tracks that pass through those saddles [73, 84]. Those
tracks would refer to the lines along which Stark saddles move as the field is
changed. Such a 1D+1D model should allow to reproduce the key feature of
45
2.4 Towards quantum model
the non-sequential double ionisation, namely, the presence of the symmetric
escape [47, 85, 86, 87, 88]. This possibility lies in the observation that as the
electrons move along the tracks away from the nucleus they also move away
from each other and thus their mutual interaction diminishes as it has the
place in a real 3D situation. This is a very crucial ingredient of the model,
because it allows the electrons to move along the polarisation axis with the
same coordinates and thus allows to mimic their correlated escape as it is
observed in experiments. This is contrary to the so called aligned-electron
model, in which electrons are confined to move only along the polarisation
axis and thus they correlated escape with equal distance from the nucleus is
suppressed by their Coulomb interaction [55, 89, 90, 91, 92]
4
2
X
0
-2
-4
-5
0
5
Z
Figure 2.14: Equipotential surfaces of the adiabatic potential for atom in a field
of amplitude F = 0.137a.u.. The Stark saddles move along the dashed lines, which
have fixed angles with respect to the polarisation axis, Z, namely α = π/6 and
α = −π/6 [66, 68].
Such a simplified 1D+1D model will be analysed in the next chapter on
the quantum mechanical grounds, and thanks to the reduced dimensionality
the relevant Schrödinger equation can be solved numerically for a realistic
set of parameters, within a relatively short period of time 1 and what is more
it can be done on the ordinary PC with a sufficient amount of RAM.
1
Time needed for a calculation depends on the accuracy that is required, that in turn
depends on the set of parameters describing the laser pulse, i.e. its frequency, amplitude,
duration.
46
Chapter 2. Classical model
Chapter 3
Quantum model
As mentioned in the previous chapter, despite the great development in the
computing technology, both in the hardware and the software, an exact solution of the time-dependent Schrördinger equation for two electrons in a
laser field still remains a hard task. It is feasible presently for not necessarily realistic laser parameters and requires very sophisticated computers [62, 63, 64, 65]. Thus, it is necessary to develop simple models in order to
implement them efficiently on easily accessible machines. One way to achieve
this goal is to reduce dimensionality of the problem. As pointed out before,
the classical analysis in the spirit of the Eckhardt-Sacha approach suggests
how to perform such a reduction without much loss in the electron-electron
correlations. Especially since the aligned-electron model [55, 59, 93, 94],
while indeed showing strong electron-electron correlations in the intermediate intensity regime [59, 94] cannot properly describe the collective motion
of electrons due to an overestimation of the Coulomb repulsion.
In the following, a simplified quantum model for the double ionisation of
atoms in the strong laser field is analysed. Model was proposed and analysed
on the classical grounds by Eckhardt and Sacha [73]. First, the model is
described, then the results concerning the ionisation yields are presented and
followed by the momenta distribution. The chapter is ended with presentation of preliminary results concerning quantum interference phenomena in
the double ionisation. Most of the contents of the following chapter is not
published yet, however introduction to the model and prove of its validity in
reproducing the experimental data can be found in an article [84].
47
48
3.1
Chapter 3. Quantum model
Physical Model
In Sec. 2.4 it has been pointed that the key idea of the simplified model is
to reduce the motion of electrons to 1D tracks that are equivalent to lines
along which Stark saddles move with the change of the field [73]. Lets recall
the Hamiltonian of the system in the full space,eq. (1.4), namely:
H=
2 2
X
p
2
−
2
|ri |
i
i=1
+
1
+ Hint ,
|r1 − r2 |
(3.1)
where Hint is the part of Hamiltonian describing the interaction with the
field. Its detailed form depends on the gauge that is used. In the following
both the velocity and the length gauges are used for the linearly polarised
laser pulse. The length gauge is used in the calculation of ionisation yields
and Hint has a form:
Hint = F (t)(z1 + z2 ),
(3.2)
whereas the velocity gauge enables to obtain momenta distributions and Hint
has a form:
Hint = A(t)(pz1 + pz2 ),
(3.3)
Rt
where the vector potential is A(t) = − 0 F (t0 )dt0 .
The pair of Stark saddles, close to which electrons have to pass in order
to escape simultaneously, for a given field amplitude F lies in the plane and
has coordinates (for the xz-plane) [66, 68, 73]:
33/4
31/4
33/4
31/4
( √ , 0, √ ) and (− √ , 0, √ ).
2 F
2 F
2 F
2 F
(3.4)
As the field amplitude changes, the saddles move along the lines that have a
constant angle with respect to the field axis (see Fig. 2.14), that is:
√
√
±33/4 /2 F
π
zS
√
=
(3.5)
=± 3→α=± ,
cot(α) =
xS
6
31/4 /2 F
where zS and xS stand for coordinates of the Stark saddle. The motion of
the electrons is confined to those lines and therefore the coordinates of the
electrons are constrained by following relations [73]:
yi = 0 and zi2 = 3x2i ,
(3.6)
and become:
√
√
1
1
3
3
r1 ) and (x2 = − r2 , 0, z2 =
r2 ).
(x1 = r1 , 0, z1 =
2
2
2
2
(3.7)
49
3.1 Physical model
With those new coordinates, eq. (3.7), the Hamiltonian of the system becomes:
2 2
X
pi
2
1
H=
−
+p
+ Hint ,
(3.8)
2
|ri |
(r1 − r2 )2 + r1 r2
i=1
where ri are electrons coordinates along the saddles’ lines (see Fig. 3.1 and
compare with Fig. 2.14). The interaction part is only slightly changed,
namely, in the length gauge it takes a form:
√
3
Hint =
F (t)(r1 + r2 ),
(3.9)
2
and in the velocity gauge is:
Hint =
√
3
A(t)(p1 + p2 ).
2
(3.10)
The ground state of the unperturbed system described by the Hamiltonian
eq. (3.8), i.e. with interaction term, Hint , set to zero, is found by means of
the imaginary time evolution. That is, time is substituted by t = −iτ and
the Schrödinger equation transforms into the diffusion equation:
∂
1
ψ = ∆ψ − V ψ.
∂τ
2
(3.11)
For any given time, τ , the solution of the eq. (3.11), may be expanded in the
basis of eigenstates, φn , of the unperturbed Hamiltonian and the energy scale
may be shifted with respect to the ground state energy, i.e. H̃ = H − E0 .
Then one obtains:
X
ψ(τ ) = φ0 +
an exp(−(En − E0 )τ )φn .
(3.12)
n=1
As time tends to the infinity, τ → ∞, only term corresponding to the ground
state, φ0 , is not damped, all other terms are the faster damped the bigger is
their distance from the ground state on the energy scale.
In all simulations the laser frequency is set to ω = 0.06 and Coulomb
interactions are smoothed in the following way [78, 79]:
1
1
→√
x
x2 + e
(3.13)
and smoothing factor is e = 0.6, resulting in the ground state energy of the
unperturbed atom E0 = −2.8. Moreover, to prevent reflections on the edges
50
Chapter 3. Quantum model
(a)
(b)
x
r2
field axis
π/6
z
r1
r2
D1
S1
D2
S4
A
S2
r1
12.5 a.u.
7 a.u.
D4
S3
D3
Figure 3.1: Geometry of the model: (a) lines along which the saddles move while
the field amplitude changes; (b) the new coordinate system and the division of the
space into regions corresponding to an atom (A), a single ion (S i ) and a double
ion (Di ) populations.
of the integration region 1 absorbing boundary conditions are included in a
form of the imaginary potential:
Vim = −iη((r1 ± x0 )α + (r2 ± x0 )α ),
(3.14)
parameters η and α are chosen appropriately to the distance from the edge,
L/2 − x0 , on which absorbing boundary conditions are supposed to act. Here
L is a size of the integration region in one direction and x0 is the distance from
nucleus at which absorbing boundary conditions start to act. The positive
sign in front of x0 corresponds to negative values of ri , the negative sign
to positive ones. Some technical details on the numerical solution of the
Schrödinger equation, both in real and imaginary time evolution, are given
in Appendix A (see A.3, A.4, A.5 and A.6).
3.2
Ionisation yield
First, the Schrödinger equation is solved in order to obtain ionisation yields
for the single and the double ionisation. To this end, following Dundas et al.
[64] regions in the configuration space corresponding to an atom, a single ion
1
Reflections originate in the fact that the edges of the integration region from the point
of view of the evolution operator are ”seen” as infinitely high walls. Therefore, the wave
function is bounced back into the integration region when it reaches the edge.
51
3.2 Ionisation yield
and a double ion, namely, A, Si and Di (see (b) panel in Fig. 3.1) are defined.
Boundaries between A and Si regions are placed at the distance of 12.5 a.u.
from the centre of the coordinate system, and boundaries between Si and
Di regions are placed at the distance of 7 a.u. from a given ri axis (see (b)
panel in Fig. 3.1). The atom is assumed to be singly ionised if one electron
is far away from and the other is in vicinity of the nucleus (the Si regions).
Similarly, the atom is assumed to be doubly ionised if both electrons are at a
large distance from the nucleus (the Di regions). The integral of the modulus
squared of the wave function over a given region determines the population
of the corresponding species, that are :
R
1. the population of atoms: PA = A |ψ|2 dr1 dr2 ,
P R
2. the population of single ions: PS = 4i=1 Si |ψ|2 dr1 dr2 ,
3. the population of double ions: PD =
P4
i=1
R
Di
|ψ|2 dr1 dr2 .
However, such an approach has at least two drawbacks, namely:
• one cannot distinguish between the sequential and the non-sequential
double ionisation, but has access to the total double ionisation yield
only;
• and once absorbing boundary conditions are applied populations in S
and D regions are smaller than they should be 2 .
The last problem could be solved by an extension of the integration region
to such a size that the electrons will not reach the edges within the evolution
time. But that in turn increases the integration time and needed memory
resources due to the size of the matrix in which the wave function is stored.
To overcome those problems without very big loses in a computation time
one may take an advantage of the geometry of the model (see the panel (b)
in Fig. 3.1). The present model enables to distinguish between the sequential
and the non-sequential double ionisation and to keep reasonable size of the
integration region thanks to the use of probability fluxes between appropriate
regions.
In the quantum mechanics one may define the continuity equation governing the change of the probability density in a given region:
∂
ρ + ∇ · j = 0,
∂t
2
The absorption at the edges may be a measure of the total ionisation only.
(3.15)
52
Chapter 3. Quantum model
where ρ = |ψ|2 is the probability density and j = − 2i (ψ ? ∇ψ − ψ∇ψ ? ) is the
probability current. It is worth stressing that the probability current has this
form only in the length gauge. In the velocity gauge it would also depend
on the vector potential, A(t). Thus the relevant Schrödinger equation will
be solved in the length gauge in order to use the present method in getting
ionisation yields for the sequential and the non-sequential double ionisation.
Integration of the continuity equation over a given region (R = {A, S, D})
and over time allows to obtain the population of the corresponding species:
Z Z
Z
PR (t) = − ( ∇ · jdr1 dr2 )dt = − FR (t)dt,
(3.16)
R
where FR (t) is the probability flux over boundaries of the region R. Hence
to get the double ionisation yield one calculates fluxes through boundaries
of Di regions. That in turn gives a possibility to distinguish the sequential
and the non-sequential double ionisation by calculating probability fluxes
over relevant boundaries. That is, one calculates the flux between regions
corresponding to single and double ions in order to get the sequential double
ionisation yield, and between regions A and Di to get the non-sequential
double ionisation yield. Moreover, the problem of absorbing boundaries is
solved by assumption that through the edges of the whole integration region
there is no flow. Such an assumption, from the point of probability fluxes,
mimics the infinite space, while in fact the wave function is absorbed at the
edges. To summarise:
• The population of single ions (SI) at time t is gotten as time integrals
of fluxes from A to Si (i = 1, 2, 3, 4) minus the fluxes from Si to Dj ;
• The non-sequential, correlated double ionisation probability (NSDI) is
obtained as time integrals of fluxes A→D2 and A→D4 .
• The non-sequential, anti–correlated double ionisation probability is obtained as time integrals of fluxes A→D1 and A→D3 (that means that
electrons’ momenta parallel to the field polarisation axis have an opposite sign in the laboratory frame, while perpendicular momenta are the
same — such a situation is quite unlikely as shown by the numerical
data).
• Integration of fluxes: Si →Dj (i, j = 1, 2, 3, 4) gives a measure of the
sequential double ionisation (SDI) process.
It is stressed that the definition of the sequential ionisation is related to the
final fluxes and can not differentiate if electrons escape fully independently
53
3.2 Ionisation yield
0,2
Fluxes
Direct integration
SI
0,15
0,1
0,05
0
0
100
200
300
400
500
600
700
Time [a.u.]
Figure 3.2: Single ions population calculated using different methods: direct
integration of the modulus squared wave function over the regions S i (dashed line)
and integration of the probability fluxes through the boundaries of the S i regions
(solid line). Absorbing boundary conditions were set at the distance 150 a.u.
from the nucleus and 5 cycle laser pulse with sine squared envelope and amplitude
F = 0.19 a.u. was used.
or before the escape the second electron has been first excited in the rescattering process.
Note that the distinction between the fluxes for sequential and nonsequential double ionisation makes the definition of NSDI more precise. The
essential difference between the fluxes for double ionisation is that in the case
of NSDI electrons interactions are significant, whereas in the case of SDI the
electrons remain sufficiently far apart that their interactions are negligible.
Thus once again (see pg. 25), it is stressed that NSDI is defined here as the
process where the electrons mutual interaction is important, i.e. the direct
flux from A to D2 and D4 .
Fig. 3.2 shows the population of single ions as a function of time obtained
with the use of both methods described above. Presented results are for the
laser pulse with amplitude F = 0.19, the envelope of the sine squared shape
and 5 cycle long. In order to stabilise the system, the evolution is continued for one additional cycle3 . Absorbing boundary conditions are set at the
distance 150 a.u. from the nucleus. As can be seen, as long as the electrons do not reach absorbing boundaries both methods give the same result.
3
Such an additional cycle is added in all calculations.
54
Chapter 3. Quantum model
Ionization yield
10
10
-4
10
0
0
-8
0.07
0.1
0.2
0.3
0.5
Field Amplitude [a.u.]
Figure 3.3: Yields for the single ionisation (circles) and the double sequential
(triangles); the double non-sequential (squares) and the anti-correlated (crosses)
lionisation as a function of the field amplitude.
Then, once electrons are absorbed there is a dramatic fall of the population
calculated with use of the direct integration of the modulus squared wave
function over the Si regions. With use of the probability fluxes this problem
is overcame.
From Fig. 3.3, where yields for different ionisation versus the field amplitude, F , are depicted, one can make a few observations:
1. The non-sequential anti-correlated electron escape is a marginal process
as expected — its non-zero yield indicates rather the fact that the flux
is calculated at the finite distance from the nucleus.
2. The sequential ionisation is always at least slightly more probable than
the non-sequential one.
3. Only the sequential ionisation curve reveals a signature of ”the knee”.
The ionisation yield was calculated for the 5 cycle pulse with the sine squared
envelope and with a fixed carrier-envelope phase.
3.2 Ionisation yield
55
The sequential process may consist of at least two paths: the independent
electron escape where, after the escape of the first electron, the other has to
get rid of the nucleus’ attraction on its own (this process becomes more significant for F above the knee) and the process where due to the re-scattering
the second electron is first excited and then, after the first electron is already
gone, leaves the ion. The re-scattering may be repeated several times and
thus lead to the increase of both the simultaneous and the sequential escapes.
The enhancement of the latter leads to the knee structure, because apart from
the sequential double ionisation that come from re-scattering events there are
still present the ionisation events that are purely sequential in their origin.
That is, the double sequential ionisation that comes from the independent
electron escapes without assistance of the re-scattering. Those events give
ionisation yields without the knee structure that can be predicted with SAE
models (see Fig 1.5).
Also the time-dependence of probability fluxes may be analysed. This
gives the insight into the dynamics of the process. The question when during
the pulse a given ionisation event takes place can be addressed. In Fig. 3.4 the
pulse shape and probability fluxes through different boundaries are shown.
It is easy to notice a strong correlation between panels (b) and (c) with
pronounced maxima for the NSDI flux occurring about half a cycle after
the SI flux maxima confirming the re-scattering scenario. First, the electron
leaves the A region - in the panel (b) in Fig. 3.4 it is seen as peaks in the single
ionisation flux near the field extrema, when the saddle for the single ionisation
is open and the ionisation itself is the most probable. This is in a good
agreement with the ADK theory (see Fig. 1.5 on pg. 17). Then the electron
is turned back to the nucleus and brings the energy as it is accelerated by
the field. It hits its parent ion and the highly excited state of an atom
is created. Then this highly excited compound decays through the single,
double sequential or non-sequential ionisation. That is seen as peaks in fluxes
for both double ionisation that appear roughly one half-cycle later than the
corresponding peaks in the single ionisation flux (see Fig. 3.4). In the first half
of the pulse the SI mainly occurs, then as there is enough time for the electron
to turn back and re-scatter, the double ionisation follows - see panels (c) and
(d) in Fig. 3.4. Moreover, both double ionisation occur close to the laser
field extrema. In the case of NSDI it means that the field is sufficiently large
to open the saddle for the symmetrical escape. That observation supports
the argument that the laser field assistance during the re-scattering event is
necessary in order to activate the non-sequential channel of decay. That fact,
that the double ionisation events occur when the field is still on is in contrast
to expectation based on the simple man model for returning electron. The
latter suggests that the electron most probably returns when the field crosses
56
2
1
0
-1
SDI flux NSDI flux
SI flux
Field
Chapter 3. Quantum model
(a)
6
4
2
0
4
(b)
(c)
2
0
4
(d)
2
0
0
1
2
3
Time in field cycles
4
5
Figure 3.4: Probability fluxes as a function of time. Panel (a) represents the field
temporal dependence for maximal field amplitude F = 0.18 and 5 cycle duration.
Panel (b) shows the flux related to the single ionisation while panels (c) and (d)
the non-sequential and the sequential double ionisation, respectively. All fluxes
are in arbitrary units (in particular SI flux maxima are typically hundreds times
higher than NSDI or SDI maxima).
the zero value (see Sec. 1.4).
If longer pulse is taken into account the sequence of events, i.e the single
ionisation followed by the double ionisation within half a cycle, seems not
to change (see Fig. 3.5). However, the longer pulse lasts the more different
ionisation signals experience significant spreading and distortion. Thus, the
temporal relation between the individual processes is not that simple anymore. Nevertheless, looking at Fig. 3.4 or Fig. 3.5 one can see that, for the
amplitude F below the knee, the sequential process is significantly activated
more or less at the same moment in the pulse when the non-sequential ionisation starts, i.e. after the first re-scattering is possible. Moreover, both NSDI
and SDI happen near the field extrema. Note, that different paths leading to
the double ionisation, including the non-sequential and all sequential paths,
in the quantum mechanics are not independent, that is they will interfere.
57
3.2 Ionisation yield
Field
0,2
(a)
0
SDI flux NSDI flux
SI flux
-0,2
(b)
1
0
(c)
1
0
(d)
1
0
0
1
2
3
4
5
Time in field cycles
6
7
8
Figure 3.5: Probability fluxes (in arbitrary units) as a function of time. Panel
(a) represents the field temporal dependence for F = 0.16. Panel (b) shows the
flux related to the single ionisation while panels (c) and (d) the non-sequential
and sequential double ionisation, respectively. The data correspond to the field
with the initial phase φ = 0 and the duration 8 cycles which is switched on and
off linearly over 2 cycles.
Such an interference pattern could be visible in the electrons’ momenta distribution, because to each point on the plane p1 p2 different paths contribute.
This aspect of the process will be discussed later on.
The time sequence of events and in particular the presence of the field
when the electrons return to the nucleus in the re-scattering event, can also be
understood from the classical dynamics. However, instead to follow Corkum
reasoning exactly, as was done in Sec. 1.4, one has to take the Coulomb field
into account (see comments on pg. 16). In Fig. 3.6 the results from a classical
trajectory calculation of the evolution of the electron in combined Coulomb
and laser fields are shown. Like Corkum did in [41] it is assumed that an
electron that tunnels out is released with zero momentum, but its position
is taken to be at the other side of the potential barrier, i.e. non-zero initial
58
Chapter 3. Quantum model
ωtr / π
2.5
(a)
2
1.5
1
4
∆E
(b)
2
0
(c)
p(t0)
2
1
0
0.5
0.6
0.7
ωt0 / π
0.8
0.9
Figure 3.6: Re-scattering in a 1-d model at F = 0.16. Panel (a) shows the return
time tr , panel (b) the excess energy at the collision moment t r and panel (c) the
tunnelling probability, obtained form a semi-classical estimate ∝ e −S where S is
the action of a tunnelling trajectory, in unscaled units. The abscissa for all panels
is the point in time where the electrons tunnel through the barrier (their initial
energy is −0.83). Dashed lines in panels (a) and (b) show the results of the model
with neglected Coulomb potential [41, 95].
position. Then classical equations of motion for that electron are integrated
until it returns to the atom. Since the process involves motion of a single
electron along the field axis, a 1-d Hamiltonian of the form:
√
3F
p2
1
H1 =
−√
+r
sin(ωt)
(3.17)
2
2
2
r +e
is assumed to describe the system. The electron that tunnels through the
Stark barrier starts with an energy −0.83 a.u., equal to the energy difference
between the ground state of He in our model and He+ ion [41].
For a weak field at the instant of tunnelling, the electron appears far
from the core, then of course it moves away in the direction pointed by the
field and as the field changes its sign it is turned back. During its return to
the nucleus the electron can acquire considerable energy as it is accelerated
by the field. However, such processes are very unlikely since the tunnelling
59
3.3 Momenta distributions
probability is negligible (see panels (b) and (c) in Fig. 3.6), i.e. returning
electrons unlikely will have large energies. Nonetheless, the relevant energy
parameter when the electron returns to the nucleus is the difference between
energy of the two electron system E(tr ) and the potential energy of the saddle
Vs (tr ) [67, 68, 73], defining:
∆E = E(tr ) − Vs (tr ),
(3.18)
where tr stands for the time of return. The data collected in Fig. 3.6 (corresponding to F = 0.16) clearly show that most of electrons return while
the field is still on in agreement with the sequence of events documented in
Fig. 3.4 and in Fig. 3.5.
For smaller F the range of positive excess energy shrinks and moves towards greater values of the tunnelling time, t0 , where the tunnelling probability is negligible. This indicates that with increasing F one should not
expect a sharp threshold behaviour for the correlated simultaneous escape
since the contributions from the correlated events slowly grow with the increase of the field amplitude. That conclusion agrees well with the results
presented in Fig. 3.3, where no threshold behaviour is observed. Note that
the re-scattering model with neglected Coulomb potentials (see (a) panel in
Fig. 3.6) reveals quantitatively different results (in this model to obtain E(tr )
the kinetic energy of the returning electron is added to the ground state energy of He+ ). That indicates importance of the Coulomb interaction during
the re-scattering event.
3.3
Momenta distributions
Apart from the total yield for the double ionisation, that reveals the knee
structure (compare Fig. 1.2 and Fig. 3.3), another test for the present model
are momenta distributions that should evidence correlated escapes of electrons. At first, to obtain a distribution of electrons’ momenta that corresponds to the double ionisation one could make the Fourier transform of the
part of the wave function localised in Di regions (see Fig. 3.1). The squared
modulus of the wave function in the momentum representation gives a momentum distribution. However, due to the fact that absorbing boundary
conditions are applied, the information contained in the final wave function
is not complete. That is, the electrons that are relatively fast, quickly reach
edges and are absorbed. The information about their momenta is lost. On
the other hand, in order not to use absorbing boundary conditions or put
them at a bigger distance one needs to enlarge the grid used to represent the
wave function. That in turn dramatically increases computing time.
60
Chapter 3. Quantum model
To overcome the problem of the lost information and to obtain the momenta distribution without great computational cost the method proposed
by Lein, Gross and Engel [92] is used. The method is based on an observation that there is a certain distance from the nucleus, say xC (in the present
calculation xC is set to 200 a.u.), at which if an electron is found it is unlikely
to be turn back. Moreover, due to the fact that xC is large and the Coulomb
potentials are weak the motion of the electron at that (or bigger) distance
is determined by the field only. That is, at that distance it can be assumed
that the electron does not interact with the nucleus and with the other electron. This method seems to be similar to the simple man’s model, however,
it is true to some extend only. The simple man’s neglects the interaction
with the nucleus and the other electron directly after tunnelling, when the
electron is still close to the nucleus. Here the distance at which the Coulomb
type interactions are neglected is rather large, assuring the correctness of the
assumption.
Neglecting the Coulomb type interactions simplifies the description a lot.
If now one performs the evolution in the velocity gauge, the interaction with
the laser field is just the multiplication by a phase in the momentum space.
That in turn gives a possibility to efficiently evolve a state in the momentum
space as if the coordination space was infinite. Namely, at the beginning,
when both electrons are ”close” to the nucleus (this region will be called
Rin ), i.e. |ri | < xC , the whole evolution is described by the Hamiltonian
eq. (3.8) with interaction part given by eq (3.10), that is:
!
√
2
X
p2i
1
3
2
Hin =
+p
+
A(t)pi −
.
(3.19)
2 +r r
2
2
|r
|
(r
−
r
)
i
1
2
1
2
i=1
Then, if for example the first electron crosses the border of xC , i.e. |r1 | > xC
and |r2 | < xC , then its evolution is simplified by neglecting the interaction
with the nucleus and the other electron, namely:
!
√
2
X
2
3
p2i
+
A(t)pi −
.
(3.20)
H1 =
2
2
|r2 |
i=1
The wave function is said to be in the R1 region. Thanks to such a simplification, the evolution of the first electron is just a multiplication by a
phase factor in the momentum space. The evolution of the other electron
still includes the interaction with the nucleus. Similarly, the simplification
is done if the second electron crosses the border instead of the first. Then
the wave function is said to be in the R2 region and the evolution of the
second electron is simplified, while in the evolution of the first one the interaction with the nucleus is kept (the Hamiltonian will have form of eq. 3.20
3.3 Momenta distributions
61
and will be labelled H2 ). In those regions the wave function is in a mixed
representation. Namely, for the electron with a simplified evolution the wave
function is in the momentum representation and for the electron that interacts with the nucleus the wave function is in the position representation. In
the momentum representation there is stored information about all possible
positions of the electron that found itself beyond the border of xC . In this
way the method mimics the infinite coordinate space for the electron beyond
xC . However, the position representation of the wave function from those
regions is not that straightforwardly accessible — this issue is discussed in
Appendix A.6.
Things get even simpler if both electrons are far away from the nucleus,
that is if |ri | > xC . Then, the whole evolution is just a multiplication by the
phase factor in the momentum space, given by the Hamiltonian:
!
√
2
X
p2i
3
Hout =
+
A(t)pi .
(3.21)
2
2
i=1
Then the wave function is said to be in the Rout region and is kept in the
momentum representation, that covers all possible positions of two electrons
that found themselves beyond the xC .
The crucial point in the method is the way in which the wave function is
transferred between the regions (Rin , R1 , R2 and Rout ) in which the evolution
is done by means of different evolution operators, i.e. Hin , H1 , H2 and Hout .
The wave function must be cut smoothly, in order to prevent reflections
(just like in the case of reflections from the edges of the integration region).
Then the part of the wave function that is transferred must be coherently
added to the wave function in an appropriate region and in an appropriate
representation. This include following transfers:
• Rin → R1 , R2 both accompanied with a one-dimensional Fourier transform;
• Rin → Rout accompanied with a two-dimensional Fourier transform;
• R1 and R2 → Rout both accompanied with a one-dimensional Fourier
transform.
The method of cutting and adding is easily understood if one considers a
1D example (more detailed description of cutting and adding in 2D can be
found in Appendix A.6). Namely, lets take a wave function, ψ(x), that has
to be smoothly cut in two parts. One part corresponds to the full evolution
and is contained in the region defined by a relation x < xC . The other part
62
Chapter 3. Quantum model
corresponds to the simplified evolution and is contained in the region defined
by a relation x > xC . The cutting can be done in the following way 4 :
α
α
ψ(x) = e−η(x−xC ) ψ(x) + (1 − e−η(x−xC ) )ψ(x) = ψin (x) + ∆ψout (x), (3.22)
where ψin is the wave function that remains after cutting out the part that
crossed the border of xC and will be still propagated without any simplification. Term denoted by ∆ψout is the part of the wave function that crossed
the border of xC and which should be added coherently to the wave function
that is evolved in a simplified way:
ψout = ψout + ∆ψout .
(3.23)
This substitution is done in every time step and of course it is preceded by
an appropriate change of the representation. The method is similar to the
use of absorbing boundary conditions, with such an exception that the part
of the wave function that has been absorbed is now evolved in a simplified
way. This simplification is possible due to the fact that the velocity gauge
is used. Then, to obtain the momenta distribution one has to collect all
parts of the wave function in the momentum representation and add them
coherently. The modulus squared of such a wave function contains then the
whole information about possible momenta in the system.
Before a deeper analysis of momenta distributions will be presented, one
may ask a question: how to extract the interesting information about the
momenta of two ionised electrons from the two electron wave function. As
has been already noted in Sec. 3.2, one can define regions of the coordinate
space that are identified with an atom, single or double ion. In order to
focus on the double ionisation, parts of the wave function corresponding
to the atom and to the single ion may be smoothly cut out from the wave
function. Those regions form a cross (see (b) panel in Fig. 3.1). Its width may
by altered and in such a way the size of regions corresponding to the atom,
the single and double may be changed. In Fig. 3.7 momenta distributions
for different cross widths are depicted. The last panel, (d), corresponds to
the wave function from the outer region, i.e. Rout . As can be seen, by the
cutting out the inner part of the wave function identified with the atom
or the single ion, one erases small momenta from the distribution. That
momenta are located along axes and close to the centre of the coordinate
system. Without much loss one could analyse only the part of the wave
function that lies in the Rout region, (see the (d) panel in Fig 3.7), because
4
Parameters η and α are chosen like in the case of absorbing boundary conditions,
appropriately to the distance between xC and the edge of the integration region
63
3.3 Momenta distributions
−3
1.5
0
1
4
2
x 10
15
10
0
2
2
−4
(b)
p [a.u.]
4
p2 [a.u.]
x 10
(a)
−2
0.5
2
p1 [a.u.]
−4
−4 −2
4
−4
x 10
15
10
0
5
−2
−4
−4 −2
0
2
p1 [a.u.]
4
(d)
4
2
0
2
p1 [a.u.]
4
−4
x 10
15
10
0
2
2
0
p [a.u.]
(c)
4
p2 [a.u.]
−4
−4 −2
5
−2
5
−2
−4
−4 −2
0
2
p1 [a.u.]
4
Figure 3.7: Electrons’ momenta distributions corresponding to the laser pulse
with the sine squared envelope, the amplitude F = 0.3 a.u., the carrier-envelope
phase φ = 0 and 5 cycles duration. Panels correspond to different width of region
that has been cut out, i.e. (a) 20 a.u., (b) 50 a.u., (c) 100 a.u. and (d) 400 a.u.
it already reveals the key feature of the correlated escape, i.e. a significant
population along the diagonal, p1 = p2 . However, comparison with the (c)
panel shows that one neglects lots of electrons moving in a correlated manner
with smaller momenta (see maxima along the diagonal close to the centre of
the coordinate system), that do not reach the Rout region before the end of
the integration. Therefore, in the following analysis mostly two cases will be
included. Namely, the wave function corresponding to the Rout region only
and the wave function that corresponds the remaining after cutting out the
part in the cross of 100 a.u. width.
Next crucial issue is the resolution at which the momentum distribution
is examined. In numerical simulations one could obtain an arbitrary good
resolution, however, at the expense of the integration time and the required
memory. On the other hand, experiments are done with some finite resolution. The resolution can also be increased, but that requires incomparably
bigger investments, not only of the time spent in a lab. In order to compare
the data obtained with the present model with the experimental ones, all
momenta distributions are convoluted with a Gaussian, which width is cho-
64
Chapter 3. Quantum model
−4
−4
x 10
15
2
10
0
5
−2
−4
−4 −2
(c)
4
0
2
p1 [a.u.]
x 10
8
4
−2
2
2
p1 [a.u.]
2
8
0
6
4
−4
0
0
x 10
10
4
2
−4
−4 −2
6
−4
−4 −2
4
−2
4
2
p2 [a.u.]
(b)
p2 [a.u.]
p2 [a.u.]
4
(d)
4
0
2
4
p1 [a.u.]
−4
x 10
2
6
0
4
−2
2
p2 [a.u.]
(a)
−4
−4 −2
0
2
p1 [a.u.]
4
Figure 3.8: Electrons’ momenta distributions corresponding to the pulse with
the sine squared envelope, the amplitude F = 0.3 a.u., the carrier-envelope phase
φ = 0 and 5 cycles duration. Panels correspond to different resolutions, i.e. (a)
0.07 a.u., (b) 0.16 a.u., (c) 0.3 a.u. and (d) 0.4 a.u. Only the wave function in the
Rout is depicted.
sen to be the one of the best presently accessible experimental resolutions,
i.e. σp = 0.07 a.u. [96]. For the matter of completeness, in Fig. 3.8 momenta
distributions obtained with different resolutions are shown. Panels (c) and
(d) resemble experimental distributions very much, even though only one
carrier-envelope phase was used. Panel (d) corresponds to the experimental
resolution obtained in the first experiment in which the momenta distributions were measured [47] (compare the left panel in Fig. 1.3). On the other
hand, panels (a) and (b) show much more complicated structures, that may
have an origin in the quantum interference of different paths leading to the
double ionisation.
In Fig. 3.9 momenta distributions corresponding to different field amplitudes are presented. The laser pulse used in the calculations had the
trapezoidal envelope and the carrier-envelope phase φ = 0. It was 8 cycles
long, just like the pulse used to obtain the probability fluxes depicted in
Fig. 3.5. As can be easily noticed (see panels (b) and (c) in Fig. 3.9) for the
amplitudes that correspond to the neighbourhood of the knee structure in
65
3.3 Momenta distributions
−4
x 10
15
x 10
5
2
4
10
0
5
4
0
2
p1 [a.u.]
−3
x 10
5
4
3
0
2
−2
1
−4
−4 −2
0
2
p1 [a.u.]
2
−2
4
1
−4
−4 −2
4
2
3
0
0
2
p1 [a.u.]
4
(d)
4
2
0.02
0
0.015
0.025
0.01
2
−4
−4 −2
p2 [a.u.]
4
2
−2
(c)
(b)
p [a.u.]
p2 [a.u.]
4
p2 [a.u.]
−8
(a)
−2
0.005
−4
−4 −2
0
2
p1 [a.u.]
4
Figure 3.9: Electron’s momenta distributions corresponding to the laser pulse with
the trapezoidal envelope, the carrier-envelope phase φ = 0 and 8 cycles duration
(two cycles for the ramp on, four cycles for the constant amplitude and two cycles
for the ramp off). Panels correspond to different field amplitudes, i.e. (a) 0.08
a.u., (b) 0.16 a.u., (c) 0.2 a.u. and (d) 0.4 a.u.
the double ionisation yield (see Fig. 3.3) distributions are concentrated along
the p1 = p2 diagonal, as expected. For small amplitude (panel (a)), as well
as, for large amplitude (panel (d)) the first and the fourth quadrants become
also significantly populated, meaning that the sequential double ionisation is
dominating.
As mentioned in Sec. 1.3 the non-sequential ionisation was also identified
via the recoil-ion momentum distribution, in which the double hump structure was observed. Thus, to make the analysis complete, in Fig. 3.10 ion’s
momentum distributions, that correspond to the electrons’ momenta distributions in Fig. 3.9, are shown. The double hump structure is clearly visible
for the field amplitude F = 0.2 a.u. The lack of the double hump structure
for the amplitude F = 0.16 a.u. is probably due to the fact that only one
carrier-envelope phase was used in obtaining presented distribution. Panel
(d) in Fig. 3.12 corresponds to the ion’s momentum distribution for the field
amplitude F = 0.16 a.u. averaged over 14 phases. The double hump structure is more visible then. Nevertheless, an important feature is that both
66
Chapter 3. Quantum model
0.3
0.25
0.2
0.15
0.1
0.05
0
-10
0.3
0.25
0.2
0.15
0.1
0.05
0
-10
Counts
(a)
-5
0.3
0.25
0.2
0.15
0.1
0.05
0
10 -10
0.3
0.25
0.2
0.15
0.1
0.05
0
10 -10
(b)
0
5
(c)
-5
0
5
10
0
5
10
(d)
-5
0
5
-5
Ion momentum [a.u.]
Figure 3.10: Normalised ion’s momentum distributions corresponding to the laser
pulse with the same parameters as in Fig. 3.9 and field amplitudes are (a) F = 0.08
a.u., (b) F = 0.16 a.u., (c) F = 0.2 a.u. and (d) F = 0.4 a.u., respectively.
distributions, for F = 0.2 a.u. and F = 0.16 a.u., are broader than the distributions for F = 0.08 a.u. and F = 0.4 a.u. The last two are clearly centred
around the zero momentum value and that, together with their narrowness,
implies that the sequential, uncorrelated process dominates.
In Fig. 3.11 electrons’ momenta distributions for different carrier-envelope
phases are depicted. Corresponding ion’s momenta distributions are shown
in Fig. 3.12. As expected, the distributions are phase-dependent. It is most
clearly seen if distributions with a π phase difference are compared (see panels
(a) and (c) in both Figs. 3.11 and 3.12). In such a case, distributions are
mirror reflections to each other [2]. However, for the 8 cycle laser pulse with
trapezoidal envelope used in the calculations the phase dependence is not that
well pronounced, even if one restricts oneself to the part of the wave function
in the Rout region. One should expect more drastic phase dependence for
shorter pulses [2]. Results for the single cycle pulse are analysed in next
section and there such a phase dependence is clearly seen (see Fig. 3.17).
What is more, the interference pattern seems not to change much with the
phase, but rather becomes more clear after averaging (see the panel (d) in
67
3.3 Momenta distributions
−4
x 10
5
2
3
0
2
−2
1
0
2
3
0
2
−2
1
2
p [a.u.]
1
−2
1
−2
4
0
2
0
2
p [a.u.]
−4
x 10
5
(c)
−2
0
2
p [a.u.]
1
3
2
1
−4
x 10
4
(d)
2
3
0
2
−2
1
2
−2
p2 [a.u.]
p2 [a.u.]
4
(b)
p [a.u.]
p2 [a.u.]
(a)
−4
x 10
−2
0
2
p [a.u.]
1
Figure 3.11: Electrons’ momenta distributions corresponding to the laser pulse
with the trapezoidal envelope, the amplitude F = 0.16 a.u. and the pulse duration
of 8 cycles. Panels correspond to different carrier-envelope phases, namely: (a) 0,
(b) 0.5π, (c) π and (d) the distribution averaged over 14 different phases.
Fig. 3.11). This observation may be misleading, because too few phases were
used in the calculations. This issue will be also addressed in next section.
The proposed model gives a chance to have insight into the dynamics of
the process of the double ionisation. One such a trial was made in a previous
section, where the time dependence of the probability fluxes was examined
(see pg. 55). Here in Fig. 3.13 it is shown how the electron’s momenta
distribution is formed in course of the pulse. Each of panels corresponds
to the modulus squared wave function from the Rout region at successive
instants of the extremal value of the field. First non-zero contribution to
the wave function in the outer region comes from the moment t ≈ 3.75 field
cycles. On the other hand, at t ≈ 2.25 field cycles the first significant nonsequential double ionisation flux appears (see (c) panel in Fig. 3.5). The
wave function that gives rise to it oscillates with the field and extends into
the outer region only about 1.5 cycles later. Taking into account that delay it
may be concluded that the first NSDI signals in the outer region, first panel
in the top row in Fig. 3.13, correspond to the first NSDI signals in the flux
analysis, (c) panel in Fig. 3.5.
68
Chapter 3. Quantum model
0.2
0.2
(a)
0.15
(b)
0.15
0.1
0.05
0.05
Counts
0.1
0
-10
0.2
0
10
-10
0.2
(c)
0.15
0
0.1
0.05
0.05
-10
0
10
0
10
0
10
(d)
0.15
0.1
0
0
-10
Ion momentum [a.u.]
Figure 3.12: Normalised ion’s momentum distributions corresponding to the laser
pulse with the same parameters as in Fig. 3.11. Panels correspond to different
carrier-envelope phases, namely: (a) 0, (b) 0.5π, (c) π and (d) the distribution
averaged over 14 different phases.
However, as already noted in previous section (see pg. 56) after a few
more cycles it is difficult give simple temporal relation between the individual events (ex. SI followed by re-scattering that gives rise to a given NSDI,
etc.) because different SI, NSDI and SDI wave packets start to interfere
with each other. Due to that interference the different ionisation signals in
Fig. 3.5 and the momentum distributions in Fig. 3.13 experience significant
spreading and distortion. That in turn, makes it impossible to identify the
wave packet that induces a given double ionisation probability flux in Fig. 3.5
with an appropriate momentum distribution in Fig. 3.13. Nevertheless, from
the analysis of Fig. 3.13 comes once again the suggestion to shorten the pulse
duration in experiments aiming on the correlated escape of electrons (compare conclusions from the classical analysis on pg. 44). It is easy to notice
in Fig. 3.13 that distributions on first 4 panels are much more concentrated
close to the p1 = p2 line than on the subsequent panels. This observation
indicates that first contributions to the overall double ionisation come from
the correlated escapes. The longer pulse lasts the more uncorrelated events
69
3.3 Momenta distributions
0.5
1
1.5
0.5
1.5
−6
p2 [a.u.]
2
4
−5
x 10
6
5
10
−5
x 10
15
−5
x 10
x 10
2
0
−2
0
1
2
0.5
1.5
−4
2.5
1
2
−4
x 10
p2 [a.u.]
2.5
3
1
2
−4
x 10
3
−4
x 10
x 10
2
0
−2
−2
0
2
p [a.u.]
1
−2
0
2
p1 [a.u.]
−2
0
2
p1 [a.u.]
−2
0
2
p1 [a.u.]
Figure 3.13: Electrons’ momenta distributions corresponding to the field amplitude F = 0.16 a.u. and the carrier-envelope phase φ = 0 at different moments
in time, i.e. 3.75, 4.25, 4.75, 5.25 field cycles (top row) and 5.75, 6.25, 6.75, 7.25
(bottom row), respectively
can appear, the sequential double ionisation becomes more important and
the distribution is no longer concentrated only along the p1 = p2 diagonal,
but spreads over all momenta.
The present results show that all key features of the double non-sequential
ionisation, i.e. the knee structure in the ionisation yield, the double hump
structure in the ion’s momentum distribution and the electrons’ momenta
distribution showing the signatures of the correlated escape, are reproduced
within the proposed simplified quantum model. That proves the validity of
the proposed model in comparison with up to date experimental results (see
Sec. 1.3). But the model can be called ”useful” when, besides explaining
present experimental results, it is able to show new directions of research,
both in the experiment and in the theory. In next section such directions are
proposed.
70
3.4
Chapter 3. Quantum model
Is it possible to measure interference in
the momenta distribution?
In almost all momenta distributions presented until now one could easily notice structures that may originate from the quantum interference phenomena.
There are several paths leading to the double ionisation that all contribute
to the final momentum distribution. All those paths from the point of view
of the quantum mechanics are not independent and interfere with each other.
Just like in the double slit interference, with such exception, that here one
has much more slits. First, one could differentiate two main paths and it
has been already done, namely the sequential and the non-sequential paths.
Next distinction could be made in the sequential path itself. The sequential
ionisation may involve ionisation of the first electron followed by the other
electron, without necessity for the re-scattering event. It may also involve
the re-scattering. The re-scattering may take place several times. Moreover,
even if the re-scattering is not involved the second electron may revisit the
parent ion once or many times and escape later. All those paths will lead to
the double ionisation, all of them will contribute to the final momenta distribution and what is crucial here all of them will interfere with each other
leading to a complicated structure in that final distribution. Also the nonsequential ionisation may happen in different moments in the pulse, as has
been shown in previous sections. Those symmetrical escapes that happen at
different instants will interfere, as well, and will give their contribution to
the interference pattern that is observed.
The pattern depends on the amplitude of the field, the pulse duration,
the carrier-envelope phase. From those three parameters the pulse duration
seems to be the most crucial. Namely, the shorter pulse the less different paths leading to the double ionisation. As already showed, both in the
classical analysis and in the quantum description, the number of sequential
escapes depends dramatically on the pulse duration. Thus one can try to
shorten the pulse to one cycle, so still allow at least one re-scattering event
and thus to allow the symmetrical escape, but at the same time to prevent
many possible sequential ionisation. The interaction with the one cycle pulse
seems to be the best candidate for testing the interference phenomena. In
Fig. 3.14 momenta distributions for different pulse duration are shown, starting from 1 cycle up to 4 cycle pulse. At first it is seen that with each added
cycle the structure complicates a lot. However, the pulse duration is not
the only reason of that changes. While one keeps the field (pulse) amplitude and the shape of the pulse constant and adds next cycles to the pulse
duration, the possible maximal field amplitude changes. The maximum of
71
3.4 Is it possible. . .
−5
x 10
15
(a)
−4
(b)
p [a.u.]
10
4
3
0
2
0
2
p [a.u.]
5
5
5
5
2
−5
−5
−5
5
x 10
(c)
12
5
10
8
0
2
6
4
−5
2
0
p1 [a.u.]
5
0
5
p [a.u.]
−4
1
−5
1
−4
1
x 10
(d)
15
5
10
0
2
0
p [a.u.]
p [a.u.]
−5
p [a.u.]
x 10
5
−5
−5
0
5
p1 [a.u.]
Figure 3.14: Electrons’ momenta distributions corresponding to the laser pulse
with the sine squared envelope, the amplitude F = 0.3 a.u., the carrier-envelope
phase φ = 0. Panels correspond to different pulse durations, i.e. (a) 1 cycle, (b) 2
cycles, (c) 3 cycles and (d) 4 cycles.
the envelope, that is set by the filed amplitude, is not the maximal possible
field amplitude. It is easily seen on the left panel in Fig. 3.15, where pulses
with all parameters equal but the pulse duration are depicted. The solid line
corresponds to the 1 cycle pulse and the maximal possible field amplitude is
Fmax = 0.17 a.u., although the pulse amplitude is set to be F = 0.3 a.u. The
broken line represents the 2 cycles pulse with Fmax = 0.22 a.u., the dotted
line the 3 cycle pulse with Fmax = 0.24 a.u. and the dash-dotted line the
4 cycle pulse with Fmax = 0.25 a.u. They correspond to panels (a)-(d) in
Fig. 3.14.
To get some insight in the changes that are seen in Fig. 3.14 the dependence on the field amplitude will be examined and as already suggested, in
the following the 1 cycle pulse will be used only. The envelope is chosen to
be sine. As can be seen in Fig. 3.16 the interference pattern becomes the
more clear the higher amplitude is used, i.e. the higher extremal amplitude
is possible. The larger amplitude the bigger momenta are registered and
the interference fringes become clearly visible in the middle of the structure.
The momenta distributions are depicted for the wave function from the Rout
72
0,3
0,2
0,2
0,1
Field [a.u.]
Field [a.u.]
Chapter 3. Quantum model
0,1
0
0
-0,1
-0,1
-0,2
-0,2
0
1
2
3
Time in field cycles
4
0
0,5
1
1,5
2
Time in field cycles
Figure 3.15: Left panel: Laser pulses of the sine squared envelope, the carrierenvelope phase set to 0 and the field amplitude F = 0.3 a.u., but different duration,
i.e. 1 cycle (solid line), 2 cycles (broken line), 3 cycles (dotted line) and 4 cycles
(dash-dotted line). Right panel: Laser pulses of the sine squared envelope, the
field amplitude F = 0.3 a.u. and the duration 1 cycle, but different phases, i.e. 0
(solid line), 0.5π (broken line) and 0.7π (dotted line).
region, i.e. |ri | > 200 a.u, only. By comparison of (a) panels in Fig. 3.14 and
in Fig. 3.16 (the same maximal possible amplitudes) one can see that the
pattern in not changed much by restricting oneself to the outer region only.
The last dependence, i.e. on the phase, basing on the previous results
(see Fig. 3.11) seems to be the weakest one. However, the shorter pulse
the stronger phase dependence should be observed - roughly speaking there
is no time in the pulse to ”forget” about the phase. In Fig. 3.17 electrons’
momenta distributions for few different phases are depicted. Previous results
suggested that distributions corresponding to the π phase difference should
be mirror reflections to each other. Distributions presented in Fig. 3.17 are
grouped in such a way that each distribution in the top row has its π-phasedifference counterpart in the bottom row, right below. The symmetry is
striking. What is more, for phases that allow two comparable extrema of the
field in a sequence, i.e. 0 and π (see solid line on the right panel in Fig. 3.15),
the interference pattern is clearly seen - see the first panel in both the top and
the bottom rows in Fig. 3.17, whereas for the other four phases (see broken
and dotted lines on the right panel in Fig. 3.15) the pattern is not visible see the second and the third panels in both the top and the bottom rows in
Fig. 3.17. For the latter phases, i.e. 0.5π, 0.7π, 1.5π and 1.7π, the double
ionisation is strongly suppressed (compare colorbars for different phases in
Fig. 3.17) due to stoppage of the re-scattering. The latter occurs because the
second field extremum is considerably weaker than the first one (see broken
73
3.4 Is it possible. . .
−5
−2
8
−4
6
4
−6
−8
−8
2
−6
−4
−2
p2 [a.u.]
x 10
3
−2
2
−4
1
−6
−8
−8
−6
−4
−2
p [a.u.]
1
2
−2
1.5
−4
1
−6
0.5
−6
0
−4
−2
0
p [a.u.]
−4
1
0
x 10
0
−8
−8
0
p [a.u.]
(c)
(b)
p2 [a.u.]
10
−4
(d)
p2 [a.u.]
p2 [a.u.]
(a)
x 10
0
−4
1
0
x 10
3
−2
2
−4
1
−6
−8
−8
−6
−4
−2
0
p [a.u.]
1
Figure 3.16: Electrons’ momenta distributions corresponding to the laser pulse
with the sine envelope, the carrier-envelope phase φ = 0 and 1 cycles duration.
Panels correspond to different maximal possible field amplitudes, i.e. (a) 0.17 a.u.,
(b) 0.19 a.u., (c) 0.23 a.u. and (d) 0.25 a.u.
and dotted lines on the right panel in Fig. 3.15). This observation suggests
that the re-scattering may be crucial for the interference.
For the sake of completeness in Fig 3.18 the phase-averaged electrons’
and ion’s momenta distributions are shown. Once again, the interference
pattern in not smoothed much (only few fringes are lost; see the left panel in
Fig. 3.18), by the averaging. And the reason may be the same as before in
the case of the 8 cycles pulse, namely, too few phases were used in averaging.
The present results are just preliminary and to fully understand the problem of the interference one needs further research. They are already carried
on. From the experimental point of view, next parameter that matters a lot,
if the interference is involved, is the resolution. All momenta distributions
that has been presented are convoluted with a Gaussian, which width was
chosen to be the resolution accessible in present experiments. That suggest
that the interference patter can be observed experimentally if other unwanted
effects are weakened. The unwanted effects come from the pulse duration or
the phase effect. Both aspect can be presently addressed experimentally as
noted in Sec. 1.3.
74
Chapter 3. Quantum model
5
10 15
2
4
−5
0.5 1.5 2.5
−5
x 10
p2 [a.u.]
6
−5
x 10
x 10
5
0
−5
5
10 15
2
4
p2 [a.u.]
−5
6
0.5 1.5 2.5
−5
−5
x 10
x 10
x 10
−5
0
5
p1 [a.u.]
−5
0
5
p1 [a.u.]
−5
0
5
p1 [a.u.]
5
0
−5
Figure 3.17: Electrons’ momenta distributions corresponding to the laser pulse
with the sine squared envelope, the amplitude F = 0.3 a.u. and the pulse duration
of 1 cycle. Panels correspond to different carrier-envelope phases, i.e. (from left
to right) top row: 0, 0.5π and 0.7π; bottom row: π, 1.5π and 1.7π.
−5
x 10
4
12.5
3.5
5
0
2
1.5
1
−5
0.5
−5
0
p1 [a.u.]
5
10
-2
2.5
Counts [10
p2 [a.u.]
]
3
7.5
5
2.5
0
-10
0
Ion momentum [a.u.]
10
Figure 3.18: The phase-averaged (over 8 phases) distributions both electrons’
(left panel) and normalised ion’s momenta (right panel) for the pulse parameters
as in Fig. 3.17
Conclusions and outlook
The present dissertation was aimed on the theoretical description of the nonsequential ionisation on both the classical and the quantum grounds. While
the classical description is easier to be treated by means of various numerical
methods, the quantum description is the most wanted. Here the classical
picture was used to address questions that arose in the experiments with
the double non-sequential ionisation of homo-nuclear molecules. From the
present analysis it can be concluded that in the final stage of the NSI process,
i.e. the decay of the highly excited compound state of the molecule, there
is no dependence neither on the molecular species nor on the orientation of
the molecule. That in turn, indicates that the difference observed in the
experiment originates in the first two stages, i.e. the tunnelling of the first
electron and the re-scattering event. In those stages the properties of the
molecular orbital, as well as, the orientation of the molecule most probably
play a crucial role. What is more, the present results suggest to use shorter
and stronger laser pulses in order to enhance the ratio of the non-sequential
to the sequential double ionisation.
The classical part included also the local analysis of the triple ionisation of
the homo-nuclear molecule. It has revealed two configurations of the saddle
that would lead to the symmetric escapes similar to those found earlier for
atoms. It showed also that the orientation of the molecule or the different
internuclear distance, while introduce difficulties in the analysis itself do not
introduce significant changes in the properties of the saddle. To complete the
analysis of the triple ionisation the numerical simulations of the final stage
of the process will be done.
Improvements of the classical description of the non-sequential ionisation
can be made by attempts to include the differences that are in the ground
state orbital of different species. The symmetry of the orbital together with
the orientation of the molecule may have influence on the tunnelling or the rescattering processes. Those differences, if they are, in turn, could be included
in the initial conditions used in the classical analysis of the NSI.
76
Conclusions and outlook
The quantum description of the non-sequential double ionisation of atoms
evolved from observations made with the use of the classical analysis. The
proposed simplified quantum model was capable to reproduce all key features of the double non-sequential ionisation, i.e. the knee structure in the
ionisation yield, the double hump structure in the ion’s momentum distribution and the electrons’ momenta distribution showing the signatures of the
correlated escape. What is worth to be stressed, is the fact that thanks to
the properly chosen geometry the Coulomb interaction between the electrons
is not overestimated, contrary to the aligned electron model, and ionisation
yields for the NSDI and the SDI could be calculated separately. Moreover,
the use of probability fluxes allowed to have an insight into the dynamics of
the process. Therefore it was possible to show that the non-sequential and
the sequential double ionisation take place near the field maxima, approximately half a cycle later than the single ionisation event. Such a time delay
gives a possibility to turn back a singly ionised electron and let it re-scatter
on its parent ion, confirming the re-scattering scenario. What is more, the
non-zero amplitude implies the presence of the saddle in the potential indicating that it plays a crucial role in the non-sequential double ionisation and
a posteriori justifying the model.
It has been possible to obtain distributions of electron’s momenta, as well
as, of the ion’s momentum. Dependence of those distributions on the field
amplitude and the carrier-envelope was analysed. Momenta distributions revealed clear signatures of the symmetrical escapes for field amplitudes close
to the knee structure. The phase dependence was not that pronounced for
the long pulse, however, for the single cycle pulse it was very significant. All
presented momenta distributions included accessible experimentally resolution giving a possibility to be verified. Once again it was possible to have an
insight into dynamics of the process through the analysis of the emergence
of the momentum distribution in the course of the laser pulse. Here also the
suggestion to use shorter laser pulses in experiments aiming on the correlated
escapes of the electrons is natural.
It was shown that the quantum model not only proved its validity. Along
with the analysis of the dependence of momenta distributions on various parameters it has been observed that they exhibit interference patterns. A preliminary analysis of the interference in the double ionisation was presented.
It revealed the dependence of the interference on the pulse duration, the
phase and the field amplitude. The analysis suggests that the re-scattering
seems to be crucial in the interference observed in the double ionisation. All
results were analysed with inclusion of the possibility for the experimental
observation via a properly chosen resolution. The questions that arise from
this analysis open a very fascinating direction of research, both for the ex-
Conclusions and outlook
77
perimentalist and for the theorists. The theoretical analysis launched by the
results presented in the dissertation is already carried on.
There is one more direction of development, namely the numerics. One
still may optimise the methods used in the present work. The code that
is written surely could be improved. All programs were written in such
a way to be run on single PC machine. The fact that here only the two
dimensional quantum model was analysed and the use of the fast Fourier
transform method resulted in relatively fast calculations. However, if one
takes into account the possibility of averaging over a reasonable ensemble
of phases, then time needed for calculations increases a lot. And either one
runs the program for a long time on a single machine or runs the program
with different set of parameter on several machines. In order to do the latter
efficiently one needs an access to a large computer farm. And if one has the
access to a computer farm or more generally to multiprocessor machines or
to machines that have multicore processors, there is also the possibility to
paralyse the code in order to increase its power. But yet this direction is
rather of the computer science in its nature.
The work presented in the dissertation was supported by Polish Government scientific founds (2005-2006) as a research project (1 P03B 099 28).
Part of simulations was realised thanks to ICM computational grant G29-10.
78
Conclusions and outlook
Appendix A
Numerical Methods
A.1
The Newton-Raphson method
The Newton-Raphson method is the simplest multidimensional root finding
method [97, 98]. Consider the set of N nonlinear equations to be solved:
fi (x) = 0,
(A.1)
where i = 1, 2, . . . , N and x = (x1 , x2 , . . . , xN ). Lets expand each of the
functions fi in the neighbourhood of x in a Taylor series:
N
X
∂fi
δxi + . . . .
fi (x + δx) = fi (x) +
∂xj
j=1
(A.2)
Terms of order higher than first are neglected and the set can be rewritten
in matrix notation as:
f (x + δx) = f (x) + J · δx,
where J is the Jacobian matrix with elements
the corrections δx that move each function fi
are sought, f (x + δx) is set to zero. Then, one
can be easily solved by LU decomposition [97,
(A.3)
defined as Jij = ∂fi /∂xj . As
simultaneously closer to zero
obtains matrix equation that
98]:
J · δx = −f .
(A.4)
The corrections are then added to the solution vector [97, 98],
x̃ = x + δx.
The whole process is iterated to convergence.
79
(A.5)
80
APPENDIX A. NUMERICAL METHODS
One has to be careful in an initial guess at the solution vector, because
the Newton-Raphson method is not always globally convergent. However, if
the derivatives of the functions can be efficiently calculated and in the neighbourhood of a root they are nonzero and continuous, the Newton-Raphson
is a good choice, thanks to its local (i.e. near a root) quadratic convergence [97, 98].
A.2
Key ideas of the Bulirsch-Stoer algorithm
Here key ideas, there are only three of them, of the Bulirsch-Stoer algorithm
will be presented, much more detailed description is easily found in the literature [97, 98]. The first idea is called the Richardson’s deferred approach to
the limit [97, 98] and roughly speaking suggests: treat the numerical solution
of the ordinary differential equation as a analytic function of the step size,
h, then probe this function for various values of the step size, fit it to some
analytic form and finally interpolate it to h = 0. The second important thing
is the choice of the fitting method [97, 98]. There are two approaches: one
is to use the rational function extrapolation, the other is to use polynomial
extrapolation. As suggested in [97, 98] the polynomial extrapolation is chosen. Last, but not least, is the idea of the modified midpoint method [97, 98],
which advances y(x) from a point x to x + H by sequence of n smaller steps,
h, which size is chosen to be h = H/n.
Then the Bulirsch-Stoer method goes as follows [97, 98, 99]:
1. rather large step is chosen to advance the solution from a point x to
x + H;
2. the step H is divided into n smaller steps, the number of sub-steps is
chosen to be 2,4,6,8,10,12,. . . ; each number of sub-steps gives a different
size of the sub-step, h;
3. the solution is advanced to cross the interval H with several different
sub-step sizes, h, say for N successive numbers of sub-steps, and then
is extrapolated to h = 0;
4. if the extrapolation returns the error estimates that are not satisfactory
one goes to higher number of sub-steps N , otherwise one goes one big
step, H, further.
There are situations in which there is an obstacle in the interval H and it
is better to make the interval smaller than go with the maximum number of
sub-steps N to infinity. Thus one has to use some kind of method to adapt
81
A.3. OPERATOR SPLITTING
the appropriate step size H and in such a way control the the Bulirsh-Stoer
algorithm. One of strategies to do so is described in detail in [97, 98].
A.3
Operator Splitting
Consider a problem described by a Schrödinger equation:
∂ψ
= Hψ,
(A.6)
∂t
where H represents some Hamiltonian operator. The evolution of the wave
function by a time step ∆t may be written in the following form:
i
ψ(t + ∆t) = exp(−iH∆t)ψ(t).
(A.7)
Suppose that the H may be written as a linear sum of n pieces, namely:
Hψ = H1 ψ + H2 ψ + . . . + Hn ψ.
(A.8)
Lets assume that for each of the partial Hamiltonian operators, Hj , the
method for evolving the function ψ for one time step is known:
ψj = exp(−iHj ∆t)ψ.
(A.9)
Then the evolution by a time step ∆t can be written as a following sequence [97, 98]:
ψ1 (t)
ψ2 (t)
= exp(−iH1 ∆t)ψ(t)
= exp(−iH2 ∆t)ψ1 (t)
...
ψ(t + ∆t) = exp(−iHn ∆t)ψn−1 (t).
(A.10)
Consequently, the evolution as a whole consists of multiple repetitions of the
above mentioned sequence. However, one has to be careful with the choice
of the splitting of the operators. This caution follows from the fact that in
general for the Hamiltonian H = T + V the total evolution operator is not
simply a product of partial evolution operators:
exp(−iH∆t) 6= exp(−iT ∆t) exp(−iV ∆t),
(A.11)
unless [T, V ] = 0. If the commutator is non zero, then the approximation (A.11) is of (∆t)2 order [100, 101].
The better choice is to split the evolution operator in a following way:
exp(−iH∆t) = exp(−iV ∆t/2) exp(−iT ∆t) exp(−iV ∆t/2).
The approximation (A.12) is of the third order in ∆t [100, 101].
(A.12)
82
APPENDIX A. NUMERICAL METHODS
A.4
Forward Time Centred Space method
Consider a diffusion equation:
∂ψ
1 ∂2
∂2
= ( 2 + 2 )ψ.
∂τ
2 ∂x
∂y
(A.13)
Lets span the function ψ on the spacial grid with an equal spacing ∆x in
each direction and let the time step be ∆t. Then discrete form of eq. (A.13)
is:
n+1
n
n
n
n
n
n
n
ψi,j
− ψi,j
− 2ψi,j
+ ψi−1,j
+ ψi,j+1
− 2ψi,j
+ ψi,j−1
1 ψi+1,j
=
.
∆τ
2
(∆x)2
(A.14)
Then one can change indices in the following way, (i, j) → i ∗ N + j = k,
where N is the number of grid points in one direction (i.e. the direction
labelled by j, however, in the presented dissertation in both directions the
number of grid points is the same). Here the indices i and j change from 0 to
N − 1. Then the index k changes from 0 to N 2 − 1 and eq. (A.14) becomes:
n
n
n
n
+ ψk+1
− 4ψkn + ψk−1
+ ψk−N
1 ψk+N
ψkn+1 − ψkn
=
.
∆τ
2
(∆x)2
(A.15)
Next, rearranging terms as follows:
1
n
n
n
n
ψkn+1 = (1 + 2A)ψkn + A(ψk+N
+ ψk+1
+ ψk−1
+ ψk−N
)
2
(A.16)
∆τ
reveals its five diagonal form. Here A = (∆x)
2 . As long as the time step and
the spacing satisfy the stability criterion:
1
∆τ ≤ (∆x)2
2
(A.17)
the method is stable [97, 98].
In solving the diffusion equation that was obtained from the Schrödinger
equation, eq. (3.11), both the Operator Splitting and the Forward Time
Centred Space (FTCS) methods were combined, i.e. first the potential part
was split from the kinetic part, then potential part is simply a multiplication
by a phase and the kinetic part is solved with FTCS. During the evolution
the wave function ψ is normalised and the energy is checked. The integration
is stopped when the energy is not changing, that condition is checked with
accuracy of 10−12 . The resulting wave function is taken as a ground state
wave function. To save the computer’s memory whole calculation can be
done with a real wave function without the loss of generality.
83
A.5. EVOLUTION WITH USE OF THE FFT ALGORITHM
A.5
Evolution with use of the FFT algorithm
The operator splitting method (see Appendix A.3) gives opportunity to use
different integrators for each of the partial Hamiltonians. That in turn allows
to achieve a better accuracy and to speed up the calculation. Consider the
Hamiltonian which consists of the kinetic and potential parts, i.e. H = T +V ,
and split the evolution operator in a following way, eq. A.12:
exp(−iH∆t) = exp(−iV ∆t/2) exp(−iT ∆t) exp(−iV ∆t/2).
(A.18)
The kinetic part, T , involves derivatives and could be approximated in a
following way (in order to be unitary):
exp(−iT ∆t) =
1 − 2i T ∆t
exp(−iT ∆t/2)
.
≈
exp(iT ∆t/2)
1 + 2i T ∆t
(A.19)
This approximation lead to the Cranck-Nicolson method, that is secondorder accurate in time and unconditionally stable [97, 98]. The application
of this method involves inverting a tridiagonal matrix in each step for each
dimension (in 2D one can reduce it to inversion of one five-diagonal matrix
in each step). But one can do better. Consider the evolution operator A.18
acting on the wave function in a following sequence:
ψ1
φ1
φ2
ψ2
ψ(t + ∆t)
=
=
=
=
=
exp(−iV ∆t/2)ψ(t),
F T (ψ1 ),
F T (exp(−iT ∆t))φ1 ,
F T −1 (φ2 ),
exp(−iV ∆t/2)ψ2 .
(A.20)
(A.21)
(A.22)
(A.23)
(A.24)
Fourier transforms in steps A.21 and A.23 can be performed with the use
of the fast Fourier transform algorithm [97, 98] by direct implementation
or with help of well developed free libraries 1 . The step A.22 is nothing
else but multiplication by a phase i.e. exp(−ip2 ∆t/2). In such a way the
only approximations are splitting the evolution operator and representing
the wave function on a grid.
A.6
Smooth cutting and coherent adding
Key ingredients of the method for evolution of two electron atom in a presence
of the linearly polarised laser field proposed by Lein, Gross and Engel [92]
1
In presented calculations the FFTW library was used; it can be found at
http://www.fftw.org and general information about the method are in [102].
84
APPENDIX A. NUMERICAL METHODS
are the smooth cutting and the coherent adding. The method is based on an
observation that there is a certain critical distance from the nucleus, say xC
(in the presented calculation xC is set to 200 a.u.), at which if an electron
is found it is unlikely to be turn back. Moreover, due to the fact that xC
is large and the Coulomb field is weak the motion of the electron from that
distance is determined by the field only. That is, at that distance it can be
assumed that the electron does not interact with the nucleus and with the
other electron.
Here it is described how the division of the space into relevant regions
and transfer between them were realised in the present calculations. Consider
the wave function, ψ(r1 , r2 ), that spreads beyond the critical distance xC at
which some of the interactions may be neglected - see Fig. A.1. It can be
written as coherent sum of four parts, namely:
1
2
ψ(r1 , r2 ) = ψin (r1 , r2 ) + ψout
(r1 , r2 ) + ψout
(r1 , r2 ) + ψout (r1 , r2 ).
(A.25)
The ψin part is the part of the wave function with both electrons ”close”
to the nucleus, |ri | < xC - the wave function is said to be in the Rin region
(see the region filled with lines in Fig. A.1). This part of the wave function
is evolved with the full-integrator, i.e. Hin in Sec. 3.3, that is without any
approximations.
1
The ψout
corresponds to the part of the wave function that describes a
situation when the first electron crossed the border of xC , i.e. |r1 | > xC and
|r2 | < xC . In such a case its interaction with nucleus is neglected, as well as,
the interaction with the other electron. The interaction between the second
electron and nucleus and the interaction of both electrons with the laser
field are not changed. This will be called the semi-simplified-integration, i.e.
H1 in Sec. 3.3, and the wave function will be said to be in the R1 region
2
(the dotted region along the r1 axis in Fig. A.1). The ψout
part has the
same meaning, but concerning the second electron. Thus the condition to be
fulfilled is |r1 | < xC and |r2 | > xC and the wave function is said to be in the
R2 region (the dotted region along the r2 axis in Fig. A.1).
The last term, ψout , corresponds to the region, where interactions of
Coulomb type are neglected. Integration in this region will be called the
full-simplified-integration, i.e. Hout in Sec. 3.3, and the wave function will be
said to be in the Rout region (in Fig. A.1 the region without a pattern) .
In every time step the whole wave function is evolved with the use of
the full, full-simplified and semi-simplified integrators. Then one cuts the
parts of the wave function that crossed borders and adds them to the wave
function in an appropriate region. First consider the wave function in the
inner region that has spread in such a way that it crossed all borders (see
85
A.6. SMOOTH CUTTING AND COHERENT ADDING
r2
r1
Figure A.1: Integration regions. Dashed lines correspond to borders between the
full-integration region (region filled with lines), R in , the full-simplified-integration
region (region without a fill pattern), R out , and the semi-simplified-integration
region (dotted region), R1 and R2 . The circle stands for the wave function.
circle in Fig A.1). It can be divided into two parts:
ψin = ψ̃in + ∆ψout .
(A.26)
ψ̃in = exp(−k[(r1 ± xC )α + (r2 ± xC )α ])ψin ,
(A.27)
First term has a form:
where k and α are parameters that have to be chosen appropriately with
respect to the distance between xC and the edge of the integration region in
order to prevent from the reflections. The sign in front of xC is chosen to be
plus when ri < 0 and minus when ri > 0. This part will become new ψin
function when the process of cutting and adding will be ended. The second
term has the form
∆ψout = (1 − exp(−k[(r1 ± xC )α + (r2 ± xC )α ]))ψin ,
(A.28)
86
APPENDIX A. NUMERICAL METHODS
and will be distributed appropriately to relevant regions. That is, to the
1
wave function ψout
is added the part that that exceeds beyond the xC in the
1
r1 coordinate. This part, ∆ψout
, is calculated in a following way:
1
∆ψout
= exp(−k[(r2 ± xC )α )∆ψout .
(A.29)
2
Similarly one finds the ∆ψout
part, namely:
2
∆ψout
= exp(−k[(r1 ± xC )α )∆ψout .
(A.30)
1
2
Once one has the ∆ψout , ∆ψout
and ∆ψout
it is possible to calculate the part
of the wave function that goes directly from the inner region to the outer
one, that is:
1
2
∆in ψout = ∆ψout − ∆ψout
− ∆ψout
.
(A.31)
In order to perform the coherent adding one needs still two parts, namely
the part of the wave function that goes from the region R1 to Rout and the
part of the wave function that goes from R2 to Rout . They are found in the
following way:
1
∆1 ψout = (1 − exp(−k[(r2 ± xC )α ))ψout
,
α
2
∆2 ψout = (1 − exp(−k[(r1 ± xC ) ))ψout .
(A.32)
(A.33)
Finally, the adding may be performed. The inner part is just substituted
by the ψ̃in . To the wave function in the regions 1 and 2 is added the part
that comes from the inner region and cut the part that goes to the outer
region. The wave function in the outer region has only incomes from all
other regions. The adding is realised by a following sequence:
ψin
1
ψout
2
ψout
ψout
→
→
→
→
ψ̃in ,
1
1
exp(−k[(r2 ± xC )α )ψout
+ ∆ψout
2
2
exp(−k[(r1 ± xC )α )ψout
+ ∆ψout
ψout + ∆in ψout + ∆1 ψout + ∆2 ψout .
(A.34)
(A.35)
(A.36)
(A.37)
Last caution, in order to take the advantage of the method in each of
the defined regions the evolution is performed in a different way and in a
different space. That is, in the inner region the whole wave function is kept
in the position representation and the evolution is performed with the use
of the operator splitting method together with FFT algorithm. In the R1
region the wave function is stored in a mixed representation, that is the first
electron’s coordinate is its momentum and the second electron’s coordinate
is its position. That mixed representation allows to mimic the infinite space
A.6. SMOOTH CUTTING AND COHERENT ADDING
87
for the first electron. The evolution for the first electron is performed in the
momentum space only, this is just a multiplication by a phase factor, and
the evolution for the second electron is accomplished by joint the operator
splitting and FFT methods. For the wave function in the R2 region situation
looks similar, the only difference is that one has to exchange the first electron
with the second. Finally in the outer region, Rout , the wave function is
stored in the momentum representation and the evolution is performed in
the momentum space. This allows to mimic infinite space for both electrons.
The wave function is easily transformable to the momentum representation only. However, to do the other way around, i.e. the obtain the wave
function in the position representation, is not that straightforward. One has
to remember that the Fourier transform is performed on the finite space and
in the algorithm the periodicity of that finite space is assumed. This problem
shows up, when one tries to transform back to the position representation
the wave function from the outer region. In the wave function ψout there is
contained information about the electrons with momenta from a given finite
interval, that is limited by the spacing of the grid ∆x in the coordinate space
in the following way:
π
,
∆x
π
=−
,
∆x
pmax =
pmin
(A.38)
(A.39)
but with corresponding positions in the infinite coordinate space. On the
other hand the size of the coordinate space, L, translates into the spacing on
the grid in the momentum space as follows:
∆p =
2π
.
L
(A.40)
That is, if now one takes N grid points in the coordinate space, that correspond to the size 2L = N ∆x, then one will obtain in the momentum space
also N grid points in the same interval, but two times denser packed. But
if one has the wave function in the momentum representation in the outer
region it corresponds to the |ri | > xC . In such a case roughly speaking
L = 2 ∗ xC , what means that the inverse Fourier transform of the ψout will
give the wave function in the coordinate space of size L. That in turn will
correspond to all possible electrons’ positions in the infinite space mapped
on the space of size L with period L. The only way to overcome this problem
is to interpolate the wave function ψout to denser grid in order to enlarge the
period L.
88
APPENDIX A. NUMERICAL METHODS
Appendix B
List of Abbreviations
ADK Amosov-Delone-Krainow
ATI the above-threshold ionisation
DA the dipole approximation
FFT the fast Fourier transform
HHG the high-order harmonics generation
MPI the multiphoton ionisation
NSDI the non-sequential double ionisation
NSI the non-sequential ionisation
SAE the single active electron model
SDI the sequential double ionisation
SI the single ionisation
89
90
APPENDIX B. LIST OF ABBREVIATIONS
Bibliography
[1] A. Rudenko et al., Phys. Rev. Lett. 93, 253001 (2004).
[2] X. Liu et al., Phys. Rev. Lett. 93, 263001 (2004).
[3] A. Baltuska et al., Nature 421, 611 (2003).
[4] E. M. Lifshitz and L. D. Landau, Mechanics (Elsevier, Oxford, 1976).
[5] E. Eremina et al., Phys. Rev. Lett. 92, 173001 (2004).
[6] K. Miyazaki, T. Shimizu, and D. Normand, J. Phys. B: At. Mol. Opt.
Phys. 37, 753 (2004).
[7] H. Friedrich, Theoretical Atomic Physics (Springer, Berlin Heildelberg,
1998).
[8] G. K. Woodgate, Elementary Atomic Structure (Oxford University
Press, Oxford, 1983).
[9] H. Haken and H. C. Wolf, The Physics of Atoms and Quanta: Introduction to Experiments and Theory (Springer, Berlin, 2000).
[10] K. C. Kulander, Phys. Rev. A 36, 2726 (1987).
[11] K. C. Kulander, Phys. Rev. A 38, 778 (1988).
[12] X. Tang, H. Rudolph, and P. Lambropoulos, Phys. Rev. Lett. 65, 3269
(1990).
[13] X. Tang, H. Rudolph, and P. Lambropoulos, Phys. Rev. A 44, R6994
(1991).
[14] A. L’Huillier, K. J. Schafer, and K. C. Kulander, J. Phys. B: At. Mol.
Opt. Phys. 24, 3315 (1991).
[15] M. Goeppert-Mayer, Ann. Phys. 9, 273 (1931).
[16] V. Hughes and L. Grabner, Phys. Rev. 79, 314 (1950).
[17] J. Brossel, B. Cagnac, and A. Kastler, C. R. Acad. Sci. Paris 273, 984
(1953).
[18] P. Kusch, Phys. Rev. 93, 1022 (1954).
91
92
BIBLIOGRAPHY
[19] W. Kaiser and C. G. B. Garrett, Phys. Rev. Lett. 7, 229 (1961).
[20] I. D. Abella, Phys. Rev. Lett. 9, 453 (1963).
[21] J. L. Hall, E. J. Robinson, and L. M. Branscomb, Phys. Rev. Lett. 14,
1013 (1965).
[22] G. Voronov and N. Delone, JETP Lett. 1, 66 (1965).
[23] P. Agostini et al., IEEE J. Quantum. Electron. QE-4, 667 (1968).
[24] R. R. Freeman and P. H. Bucksbaum, J. Phys. B: At. Mol. Opt. Phys.
24, 325 (1991).
[25] T. W. B. Kibble, Phys. Rev. Lett. 16, 1054 (1966).
[26] P. H. Bucksbaum, M. Bashkansky, and T. J. McIlrath, Phys. Rev. Lett.
58, 349 (1987a).
[27] G. Mainfray and C. Manus, Rep. Prog. Phys. 54, 1333 (1991).
[28] K. Burnett, V. C. Reed, and P. L. Knight, J. Phys. B: At. Mol. Opt.
Phys. 26, 561 (1993).
[29] P. Agostini et al., Phys. Rev. Lett. 42, 1127 (1979).
[30] B. W. Shore and P. L. Knight, J. Phys. B: At. Mol. Phys. 24, 325
(1987).
[31] A. L’Huillier, L. A. Lompre, G. Mainfray, and C. Manus, Phys. Rev.
Lett. 48, 1814 (1982).
[32] A. L’Huillier, L. A. Lompre, G. Mainfray, and C. Manus, Phys. Rev.
A 27, 2503 (1983).
[33] A. L’Huillier, L. A. Lompre, G. Mainfray, and C. Manus, J. Phys. B:
At. Mol. Phys. 16, 1363 (1983).
[34] B. Walker et al., Phys. Rev. Lett. 73, 1227 (1994).
[35] D. N. Fittinghoff, P. R. Bolton, B. Chang, and K. C. Kulander, Phys.
Rev. Lett. 69, 2642 (1992).
[36] in Super-Intense Laser-Atom Physics, Proceedings of the NATO Advanced Research Workshop, Han-sur-Lesse, Belgium, 1993, edited
by B. Piraux, A. L’Huillier, and K. Rza̧żewski (Plenum Press, New
York, 1993).
[37] in Super-Intense Laser-Atom Physics, Proceedings of the NATO Advanced Research Workshop, Han-sur-Lesse, Belgium, 2000, edited
by B. Piraux and K. Rza̧żewski (Kluwer Academic Publishers, Dordrecht, 2001).
BIBLIOGRAPHY
93
[38] K. J. Schafer, B. Yang, L. F. DiMauro, and K. C. Kulander, Phys. Rev.
Lett. 70, 1599 (1993).
[39] B. Yang et al., Phys. Rev. Lett. 71, 3770 (1993).
[40] T. Auguste et al., J. Phys. B: At. Mol. Opt. Phys. 25, 4181 (1992).
[41] P. B. Corkum, Phys. Rev. Lett. 71, 1994 (1993).
[42] C. Cornaggia and P. Hering, J. Phys. B: At. Mol. Opt. Phys. 31, L503
(1998).
[43] C. Guo, M. Li, J. P. Nibarger, and G. N. Gibson, Phys. Rev. A 58,
R4271 (1998).
[44] C. Guo, M. Li, J. P. Nibarger, and G. N. Gibson, Phys. Rev. A 61,
033413 (2000).
[45] R. Dörner et al., Phys. Rep. 330, 95 (2000).
[46] J. Ullrich et al., J. Phys. B: At. Mol. Opt. Phys. 30, 2917 (1997).
[47] T. Weber et al., Nature 405, 658 (2000).
[48] T. Weber et al., Phys. Rev. Lett. 84, 443 (2000).
[49] T. Weber et al., J. Phys. B: At. Mol. Opt. Phys. 33, L128 (2000).
[50] R. Moshammer et al., Phys. Rev. Lett. 84, 447 (2000).
[51] D. Zeidler et al., Phys. Rev. Lett. 95, 203003 (2005).
[52] A. Becker and F. H. M. Faisal, J. Phys. B: At. Mol. Opt. Phys. 29,
L197 (1996).
[53] A. Becker and F. H. M. Faisal, J. Phys. B: At. Mol. Opt. Phys. 32,
L335 (1999).
[54] J. B. Watson et al., Phys. Rev. Lett. 78, 1884 (1997).
[55] W.-C. Liu, J. H. Eberly, S. L. Hann, and R. Grobe, Phys. Rev. Lett.
83, 521 (1999).
[56] K. C. Kulander, K. J. Schafer, and J. L. Krause, in Super-Intense
Laser-Atom Physics, Proceedings of the NATO Advanced Research
Workshop, Han-sur-Lesse, Belgium, 1993, edited by B. Piraux, A.
L’Huillier, and K. Rza̧żewski (Plenum Press, New York, 1993).
[57] M. V. Ammosov, N. B. Delone, and V. P. Krainov, Zh. Eksp. Teor.
Foz. 91, 2008 (1986).
[58] T. Brabec, M. Y. Ivanov, and P. B. Corkum, Phys. Rev. A 54, R2551
(1996).
94
BIBLIOGRAPHY
[59] R. Panfili, S. L. Haan, and J. H. Eberly, Phys. Rev. Lett. 89, 113001
(2002).
[60] X. Liu and C. F. de Morisson Faria, Phys. Rev. Lett. 92, 133006 (2004).
[61] U. Eichmann et al., Phys. Rev. Lett. 84, 3550 (2000).
[62] J. Parker, K. T. Taylor, C. W. Clark, and S. Blodgett-Ford, J. Phys.
B: At. Mol. Opt. Phys. 29, L33 (1996).
[63] J. Parker, E. S. Smyth, and K. T. Taylor, J. Phys. B: At. Mol. Opt.
Phys. 31, L571 (1998).
[64] D. Dundas, K. T. Taylor, J. S. Parker, and E. S. Smyth, J. Phys. B:
At. Mol. Opt. Phys. 32, L231 (1999).
[65] J. S. Parker, B. J. S. Doherty, K. J. Meharg, and K. T. Taylor, J. Phys.
B: At. Mol. Opt. Phys. 36, L393 (2003).
[66] B. Eckhardt and K. Sacha, Physica Scripta T90, 185 (2001).
[67] B. Eckhardt and K. Sacha, Europhys. Lett. 56, 651 (2001).
[68] K. Sacha and B. Eckhardt, Phys. Rev. A 63, 043414 (2001).
[69] K. Sacha and B. Eckhardt, Phys. Rev. A 64, 053401 (2001).
[70] K. Sacha and B. Eckhardt, J. Phys. B: At. Mol. Opt. Phys. 36, 3923
(2003).
[71] J. S. Prauzner-Bechcicki, K. Sacha, B. Eckhardt, and J. Zakrzewski,
Phys. Rev. A 71, 033407 (2005).
[72] J. S. Prauzner-Bechcicki, K. Sacha, and B. Eckhardt, Las. Phys. 15,
497 (2005).
[73] B. Eckhardt and K. Sacha, submited to J. Phys. B: At. Mol. Opt. Phys.
.
[74] G. H. Wannier, Phys. Rev. 90, 817 (1953).
[75] R. Peterkop, J. Phys. B: At. Mol. Phys. 4, 513 (1971).
[76] A. R. P. Rau, Phys. Rep. 110, 369 (1984).
[77] J. M. Rost, Phys. Rep. 297, 271 (1998).
[78] Q. Su, J. H. Eberly, and J. Javanainen, Phys. Rev. Lett. 64, 862 (1990).
[79] V. C. Reed, P. L. Knight, and K. Burnett, Phys. Rev. Lett. 67, 1415
(1991).
[80] J. M. Rost, Physica E 9, 467 (2001).
[81] K. Kulander, J. Cooper, and K. Schafer, Phys. Rev. A 51, 561 (1995).
BIBLIOGRAPHY
95
[82] J. Muth-Böhm, A. Becker, and F. H. M. Faisal, Phys. Rev. Lett. 85,
2280 (2000).
[83] F. Grasbon et al., Phys. Rev. A 63, 041402(R) (2001).
[84] J. S. Prauzner-Bechcicki, K. Sacha, B. Eckhardt, and J. Zakrzewski,
submited to Phys. Rev. Lett. .
[85] M. Weckenbrock et al., J. Phys. B: At. Mol. Opt. Phys. 34, L449 (2001).
[86] B. Feuerstein et al., Phys. Rev. Lett. 87, 043003 (2001).
[87] R. Moshammer et al., Phys. Rev. A 65, 035401 (2002).
[88] R. Moshammer et al., J. Phys. B: At. Mol. Opt. Phys. 36, L113 (2003).
[89] R. Grobe and J. H. Eberly, Phys. Rev. A 48, 4664 (1993).
[90] D. Bauer, Phys. Rev. A 56, 3028 (1997).
[91] D. G. Lappas and R. van Leeuwen, J. Phys. B 31, L249 (1998).
[92] M. Lein, E. K. U. Gross, and V. Engel, Phys. Rev. Lett. 85, 4707
(2000).
[93] C. Szymanowski et al., Phys. Rev. A 61, 055401 (2000).
[94] S. L. Haan, P. S. Wheeler, R. Panfili, and J. H. Eberly, Phys. Rev. A
66, 061402(R) (2002).
[95] A. Becker, R. Dörner, and R. Moshammer, J. Phys. B: At. Mol. Opt.
Phys. 38, S753 (2005).
[96] M. Weckenbrock et al., Phys. Rev. Lett. 92, 213002 (2004).
[97] W. H. Press, S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery, Numerical Recipes in C: The art of Scientific Computing (Cambridge
University Press, New York, 2002).
[98] W. H. Press, S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery,
Numerical Recipes in FORTRAN: The art of Scientific Computing
(Cambridge University Press, New York, 1995).
[99] J. Stoer and R. Bulirsch, Introduction to Numerical Analysis (SpringerVerlag, New York, 1980).
[100] R. P. Feynman, Rev. Mod. Phys. 48, 367 (1948).
[101] K. E. Schmidt and M. A. Lee, Phys. Rev. E 51, 5495 (1995).
[102] M. Frigo and S. G. Johnson, Proc. ICASSP 1998 3, 1381 (1998).