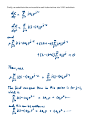Download 3.13 The Hamiltonian for two interacting particles At the atomic scale

3.13 The Hamiltonian for two interacting particles
At the atomic scale, the hydrogen atom comprises the simplest two particle system and
since we are about to derive the complete solutions to the 3D Schrödinger equation for the
central potential (i.e. the hydrogen atom), this is a good time to review what the
Hamiltonian for a two particle system looks like and how it is derived.
The vector diagram below describes the relative positions of two particles with masses m1
and m2, as they are observed in the laboratory frame.
The relative position of the particles is
And the potential between them is
The position of the center of mass of the two particle system is
with
We now construct the classical Hamiltonian, starting from the classical Lagrangian:
To find the Hamiltonian, we can then do the following (as long as the potential is velocity
independent):
From which we find that
The real meat of the Hamiltonian is in the relative term. The center of mass term
represents physics that is essentially equal to that of a single particle. If we ignore the
center of mass motion, then we obtain the Hamiltonian for a particle in a central potential
or for a system of two particles as a closed system.
This is the same expression for H that we were using all along, since section 3.4, but now,
instead of the mass of a single particle m , we have the so called reduced mass μ for two
particles in relative motion.
We will continue where we left off in section 3.12 but will now use the reduced mass in our
calculations. Numerically this makes no difference for the hydrogen atom, since the proton
is so much more massive than the electron, so that the reduced mass is essentially equal to
the electron mass:
3.14 Exact solutions to the 3D Schrödinger equation (The hydrogen atom)
To find the general solution to the radial equation (with or without the limits taken in the
previous section), we postulate that there is an additional function of r (or ρ) multiplying
the solutions we obtained in the previous section. Of course, it’s not much of a stretch to
imagine that this must be the case, since in the general case, we have additional terms of r
(or ρ) in the radial equation which must be canceled out somehow. Then we could write the
general solution as
(I am dropping the EL subscript for reasons of notational simplicity in what is to come)
In addition, we know that any such function (as long as it is well behaved locally) can be
expanded in a power series. So we write it as
Before using the series solution, however, lets substitute the general solution from above
(eqn. 3.14.1) into the eqn. 3.12.1 and simplify that down first. Let the slugfest begin…
So, putting this into eqn 3.12.1 gives
Finally, we substitute the series solution and its derivatives into 3.14.3 and obtain
Since this has to be true for all powers and values of ρ we ultimately have the requirement
that
From this recursion relation, we see that,
for bound states, the series
diverges for large j at large ρ, unless the series terminates at some point. This means that
there must be some value for j such that
or, from the above recursion relation
Then, defining the principal quantum number to be
We have
So that the principal quantum number n determines the maximum value of j for a given
value of orbital angular momentum l . So that
for each possible value of orbital angular momentum l, which is determined by the fact that
j can’t be negative. So
From our earlier definition of λ , we then have