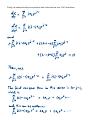* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 3.13 The Hamiltonian for two interacting particles At the atomic scale
Perturbation theory wikipedia , lookup
Renormalization group wikipedia , lookup
Geiger–Marsden experiment wikipedia , lookup
Dirac equation wikipedia , lookup
Wave function wikipedia , lookup
Renormalization wikipedia , lookup
Path integral formulation wikipedia , lookup
Double-slit experiment wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Particle in a box wikipedia , lookup
Schrödinger equation wikipedia , lookup
Scalar field theory wikipedia , lookup
Dirac bracket wikipedia , lookup
Electron scattering wikipedia , lookup
Wave–particle duality wikipedia , lookup
Identical particles wikipedia , lookup
Canonical quantization wikipedia , lookup
Matter wave wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Elementary particle wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Molecular Hamiltonian wikipedia , lookup
3.13 The Hamiltonian for two interacting particles At the atomic scale, the hydrogen atom comprises the simplest two particle system and since we are about to derive the complete solutions to the 3D Schrödinger equation for the central potential (i.e. the hydrogen atom), this is a good time to review what the Hamiltonian for a two particle system looks like and how it is derived. The vector diagram below describes the relative positions of two particles with masses m1 and m2, as they are observed in the laboratory frame. The relative position of the particles is And the potential between them is The position of the center of mass of the two particle system is with We now construct the classical Hamiltonian, starting from the classical Lagrangian: To find the Hamiltonian, we can then do the following (as long as the potential is velocity independent): From which we find that The real meat of the Hamiltonian is in the relative term. The center of mass term represents physics that is essentially equal to that of a single particle. If we ignore the center of mass motion, then we obtain the Hamiltonian for a particle in a central potential or for a system of two particles as a closed system. This is the same expression for H that we were using all along, since section 3.4, but now, instead of the mass of a single particle m , we have the so called reduced mass μ for two particles in relative motion. We will continue where we left off in section 3.12 but will now use the reduced mass in our calculations. Numerically this makes no difference for the hydrogen atom, since the proton is so much more massive than the electron, so that the reduced mass is essentially equal to the electron mass: 3.14 Exact solutions to the 3D Schrödinger equation (The hydrogen atom) To find the general solution to the radial equation (with or without the limits taken in the previous section), we postulate that there is an additional function of r (or ρ) multiplying the solutions we obtained in the previous section. Of course, it’s not much of a stretch to imagine that this must be the case, since in the general case, we have additional terms of r (or ρ) in the radial equation which must be canceled out somehow. Then we could write the general solution as (I am dropping the EL subscript for reasons of notational simplicity in what is to come) In addition, we know that any such function (as long as it is well behaved locally) can be expanded in a power series. So we write it as Before using the series solution, however, lets substitute the general solution from above (eqn. 3.14.1) into the eqn. 3.12.1 and simplify that down first. Let the slugfest begin… So, putting this into eqn 3.12.1 gives Finally, we substitute the series solution and its derivatives into 3.14.3 and obtain Since this has to be true for all powers and values of ρ we ultimately have the requirement that From this recursion relation, we see that, for bound states, the series diverges for large j at large ρ, unless the series terminates at some point. This means that there must be some value for j such that or, from the above recursion relation Then, defining the principal quantum number to be We have So that the principal quantum number n determines the maximum value of j for a given value of orbital angular momentum l . So that for each possible value of orbital angular momentum l, which is determined by the fact that j can’t be negative. So From our earlier definition of λ , we then have