* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Redwoods Symphony - Eastern Washington University
Survey
Document related concepts
Location arithmetic wikipedia , lookup
Positional notation wikipedia , lookup
Infinitesimal wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Georg Cantor's first set theory article wikipedia , lookup
Foundations of mathematics wikipedia , lookup
Ethnomathematics wikipedia , lookup
Bernoulli number wikipedia , lookup
Collatz conjecture wikipedia , lookup
Large numbers wikipedia , lookup
Real number wikipedia , lookup
Transcript
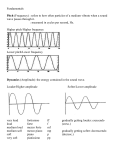
Mathematical Scaling Operations for Composing Music from Numbers Presented by Jonathan Middleton Assistant Professor of Composition and Theory Eastern Washington University Pacific Northwest Chapter, College Music Society 2006 Annual Meeting - Douglas College - Vancouver, British Columbia Mathematical content from: “Composing Music from Numbers” By Jonathan Middleton and Diane Dowd Compositions:” Redwoods Symphony” and “Spirals” by Jonathan Middleton Web-based application: http://musicalgorithms.ewu.edu/ Topic Goals I. Introduce Basic Scaling Processes Numbers Source Set » Scaled to » Instrument Range Set A. Division Operation B. Modulo Operation II. Listen to the effects of each scaling process A. Redwoods Symphony B. Dreaming Among Thermal Pools and Concentric Spirals Pitch Range in Numbers • The scaling process for mapping a source set of numbers to an instrument’s range relies on a numeric representation of the range of each instrument. • Here, we see the keyboard range 1-88. The numbers for piano keys can be used for scaling pitch ranges for other instruments, since most instrument ranges are encompassed in the piano range. The alternative would be to use the standard MIDI range of 128 pitches (middle C is 60). Scaling Operations • Two basic methods for mapping a set of numbers to new numeric range are 1) the Division Operation, and 2) the Modulo Operation. We can see at a glance that the division operation follows the contours of the Dow averages. The Division Operation • The division operation is based on a proportionate representation of the source set of integers. • The division operation works by a process of expansion or reduction from a source range of numbers to a destination pitch (or rhythmic) range. • • That is, the source number distance e.g. 0-9 can expand to a broad instrument range (0-88 for the piano), or reduce to a small motivic range 0-3. If we take for example the number set [64, 81, 100, 121, 200] and apply a division operation to the pitch range 28-52, the numbers from the set correspond to pitches 28, 31,34, 38, 52 [DEMO upon request] http://musicalgorithms.ewu.edu/ • [offline apple tab to import algorithm] The Division Operation is anchored by a Scaling Ratio Division Calculation • the expression to calculate the pitch p for a given source number s is the following: Trans to Mod Like the division operation, the modulo scaling process requires that a fixed range of pitch numbers be designated. The number of pitches in the range defines the cycle number to be used, e.g., a pitch range of 3 pitches would define the cycle number 3. Note: Modulo represents a cyclical form of counting. Mod “3” refers to the number of numbers in a span of 3, i.e. 0-2, or 1-3, or 99-101. In the span 28-52 there are 25 numbers (not 24). Modulo Operation • Modular arithmetic offers a cyclical approach to translating source numbers into pitches. • The entire operation is based on a system of counting (cycling) from the lowest to the highest number in the cycle number range. For example, cycle number 3 creates the cyclic pattern: 1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3, …. If a sequence of numbers is translated to a cycle of 3 numbers, all of the numbers will be congruent () to 1’s, 2’s or 3’s. Modulo in Detail • • In the modulo operation, we can find a pitch for any source number by locating the pitch number that is congruent to the source number. This process of matching pitches with source numbers by congruence must begin by establishing a cyclical pattern of counting within the pitch range. As an example, again consider the set of source numbers [64, 81, 100, 121, 200]. If we wish to scale these numbers to the pitch range 28 to 52 (called mod 25), we proceed through the following steps: 64: p = 14 81: p = 6 100: p = 0 121: p = 21 200: p = 0 + 28 + 28 + 28 + 28 + 28 = 42 = 34 = 28 = 49 = 28 The pitches, within the range 28 to 52, that are associated with the source numbers [64, 81, 100, 121, 200] are the pitches (or modular numbers) [42, 34, 28, 49, 28]. • [DEMO upon request] • http://musicalgorithms.ewu.edu/ • [offline apple tab to import algorithm] Modulo Calculation Redwoods Symphony Movement 1 Main theme in xylophone from tctcaagcac ataaaaaggc cattcgaaga gctgctgtca attcatttgg ttacattgct cgtgctcttg gtcctcaaga tgtacttcaa gtcttgctca ccaatttgcg agttcaagaa The DNA comes from LOCUS AY562165 of the National Center for Biotechnology Information (NCBI), a databank for research in genetics.* Each DNA letter A-T-C-G was associated with a number A=0, T=1, C=2, and G=3. *AUTHORS Bruno,D. and Brinegar,C.“Microsatellite markers in coast redwood (Sequoia sempervirens)” JOURNAL Mol. Ecol. Notes 4 (3), 482-484 (2004) Redwoods Symphony Movement 1, page 2 • The Redwood DNA was used to create a theme for xylophone by mapping the DNA “numbers” 0-3 to the numeric range 41-59 which falls within the xylophone’s numeric pitch range 40 (C4) to 76 (C7). There are three ranges to choose from depending on the model of the instrument. • A scaling process called the division operation was used to convert, or map, numbers 0-3 (DNA input) to numbers 41-59 (xylophone output). The pitch output was modified so that 53 becomes zero and 47 becomes 46. [DEMO] • CMS2006/ConPresentation/Redwood DNA.rtf • http://musicalgorithms.ewu.edu/algorithms/DNA seq.html [Offline apple tab to DNA algorithm] The DNA source numbers were also used for scaling range of durations : 1-3 with a modulo operation. Xylophone theme from Redwood DNA Spirals work-in-progress Commissioned by John Marshall and Lynne Feller Marshall • • • • • • uses a set of integers drawn from spiral coordinates. The integers were found at a Web site called the Online Encyclopedia of Integer Sequences (see URL: http://www.research.att.com/projects/OEIS?A num=A033988). The ID Number is A033988 and the description is as follows : “write 0,1,2,... in clockwise spiral, writing each digit in separate square; sequence gives numbers on positive y axis.” The authors provide the following example: 131416... 245652... 130717... 121862... 101918... From Spiral Numbers to Cello Sequence: 0,5,1,4,3,7,8,0,4,7,7,1,2,6,2,1,8,7,4,2,6,1, 8,9,2,7,6,0,6,5,1,2,0,4,1,5,8,5,1,8,8,8,2,1, 2,3,2,4,9,0,2,8,9,9,3,3,2,0,3,7,9,3,4,2,8,8, 4,7,1,5,5,3,7,4,5,9,7,5,6,5,9,8,7,1,5,3,7,8, 4,0,8,5,6,9,9,3,1,0,9,8,1,1,6,9,9 The 104 numbers were scaled by a division operation within the range of the cello to create walking bass line. The cello range was 16 (low C2) to 59 (high G5). The first 28 numbers go from zero to zero: 0,5,1,4,3,7,8,0,4,7,7,1,2,6,2,1,8,7,4,2,6,1, 8,9,2,7,6,0 The pitch output is: 16,39,20,35,30,49,54,16,35,49,49,20,25, 44,25,20,54,49,35,25,44,20,54,59,25,49, 44,16 Bibliography Explore how other Composers Create Music from Numbers D. Cummerow’s Website http://www.geocities.com/Vienna/9349/index.html T. Dukich’s Website http://tomdukich.com T. Johnson, Self-Similar Melodies (Paris: Editions 75, 1996). I. Peterson article MathTrek http://www.sciencenews.org/articles/20050917/mathtrek.asp Introductory Information on Algorithmic Composition K. H. Burns, “The History and Development of Algorithms in Music Composition, 1957-1993,” Ph.D. Dissertation (Ball State University, 1994). C. Roads, The Computer Music Tutorial (Cambridge: MIT Press, 1996). Connections between Music and Mathematics G. Assayag, H. G. Feichtinger and J. F. Rodrigues, eds., Mathematics and Music: A Diderot Mathematical Forum (New York: Springer-Verlag, 2002). J. Flauvel, R. Flood and R. Wilson, eds., Music and Mathematics: From Pythagoras to Fractals (Oxford: Oxford University Press, 2003). For information on “Composing Music from Numbers” or commercial recordings of Redwoods Symphony and Spirals contact me at [email protected] Redwoods Symphony will be available in June through ERM Media “Masterworks of the New Era” Kiev Philharmonic