Download Chapter 2

Segment Measure and
Coordinate Graphing
CHAPTER 2
Real Numbers and Number Lines
SECTION 2-1
NATURAL NUMBERS set of counting numbers
{1, 2, 3, 4, 5, 6, 7, 8…}
WHOLE NUMBERS –
set of counting numbers
plus zero
{0, 1, 2, 3, 4, 5, 6, 7, 8…}
INTEGERS –
set of the whole numbers
plus their opposites
{…, -3, -2, -1, 0, 1, 2, 3, …}
RATIONAL NUMBERS numbers that can be
expressed as a ratio of two
integers a and b and
includes fractions,
repeating decimals, and
terminating decimals
EXAMPLES OF RATIONAL
NUMBERS
0.375 = 3/8
0.66666…= 2/3
0/5 = 0
IRRATIONAL NUMBERS numbers that cannot be
expressed as a ratio of two
integers a and b and can still
be designated on a number
line
REAL NUMBERS
Include both rational and
irrational numbers
Coordinate
 The number that
corresponds to a point on a
number line
Absolute Value
 The number of units a
number is from zero on
the number line
Segments and Properties of
Real Numbers
SECTION 2-2
Betweeness
 Refers to collinear points
 Point B is between points
A and C if A, B, and C are
collinear and AB + BC =
AC
Example
 Three segment measures are
given. Determine which point
is between the other two.
 AB = 12, BC = 47, and AC = 35
Measurement and
Unit of Measure
 Measurement is composed of
the measure and the unit of
measure
 Measure tells you how many
units
 Unit of measure tells you
what unit you are using
Precision
 Depends on the smallest
unit of measure being used
Greatest Possible Error
 Half of the smallest unit
used to make the
measurement
Percent Error
Greatest Possible Error
measurement
x
100
Congruent Segments
SECTION 2-3
Congruent Segments
 Two segments are
congruent if and only if
they have the same length
Theorems
 Statements that can be
justified by using logical
reasoning
Theorem 2-1
 Congruence of segments is
reflexive
Theorem 2-2
 Congruence of segments is
symmetric
Theorem 2-3
 Congruence of segments is
transitive
Midpoint
 A point M is the midpoint of a
segment ST if and only if M is
between S and T and SM = MT
Bisect
 To separate something
into two congruent parts
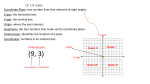
The Coordinate Plane
SECTION 2-4
Coordinate Plane
 Grid used to locate points
 Divided by the y-axis and
the x-axis into four
quadrants
 The intersection of the
axes is the origin
 An ordered pair of numbers
names the coordinate of a
point
 X-coordinate is first in the
ordered pair
 Y-coordinate is second in
the ordered pair
Postulate 2-4
 Each point in a coordinate
plane corresponds to exactly
one ordered pair of real
numbers. Each ordered pair
of real numbers corresponds
to exactly one point in a
coordinate plane.
Theorem 2-4
 If a and b are real numbers,
a vertical line contains all
points (x, y) such that
x = a, and a horizontal line
contains all points (x, y)
such that y = b.
Midpoints
SECTION 2-5
Theorem 2-5
Midpoint formula for a line
 On a number line, the
coordinate of the midpoint
of a segment whose
endpoints have coordinate
a and b is a+b.
2
Theorem 2-6
Midpoint formula for a
Coordinate Plane
 On a coordinate plane, the
coordinates of the midpoint of a
segment whose endpoints have
coordinates (x1, y1) and (x2, y2) are
(x1 + x2 , y1 + y2)
2
2