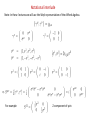* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Supersymmetry (SUSY)
Theory of everything wikipedia , lookup
History of quantum field theory wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Dirac equation wikipedia , lookup
Introduction to quantum mechanics wikipedia , lookup
Renormalization group wikipedia , lookup
Derivations of the Lorentz transformations wikipedia , lookup
Canonical quantization wikipedia , lookup
Noether's theorem wikipedia , lookup
Quantum chromodynamics wikipedia , lookup
Higgs mechanism wikipedia , lookup
Technicolor (physics) wikipedia , lookup
Future Circular Collider wikipedia , lookup
Elementary particle wikipedia , lookup
Photon polarization wikipedia , lookup
Two-dimensional conformal field theory wikipedia , lookup
Tensor operator wikipedia , lookup
Electron scattering wikipedia , lookup
Representation theory of the Lorentz group wikipedia , lookup
Vertex operator algebra wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
Standard Model wikipedia , lookup
Spin (physics) wikipedia , lookup
Mathematical formulation of the Standard Model wikipedia , lookup
Angular momentum operator wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Oscillator representation wikipedia , lookup
Lie algebra extension wikipedia , lookup
Quantum group wikipedia , lookup
An Exceptionally Simple Theory of Everything wikipedia , lookup
Scalar field theory wikipedia , lookup
Grand Unified Theory wikipedia , lookup
Minimal Supersymmetric Standard Model wikipedia , lookup
Supersymmetry (SUSY) Lecture 1 Preliminary Remarks Cautions Based on 7 “doppel stunde” lectures I gave in Dresden, 13-14 one hour lectures. However I can go faster or slower depending on prior knowledge, feedback is essential. I will only cover N=1 global supersymmetry here, which is most relevant to phenomenology. For local or extended SUSY you will need to read further. There are many conventions, but understanding shouldn’t depend on this. I will try to stick to one choice and be consistent, but I may slip on occasion, so beware. Comments Supersymmetry is a deep and rich subject, I have been studying it for about 7 years, but I am still learning. We have only a few lectures and cannot teach it all. We have not established that SUSY is realised in nature. SUSY is currently searched for at the Large Hadron Collider at CERN. If such “low-energy” SUSY is discovered this will be tremendously exciting! However SUSY may be realised in nature in other ways (a symmetry broken at much higher energies) and can be significant for other reasons. I already provided extensive discussion of the motivation in my SUSY talk (slides here: http://www.physics.adelaide.edu.au/cssm/seminars/abstracts/abstracts.html#20111012 ) Here I just assume you are motivated to learn SUSY, but don’t know any of the details. Literature • Stockinger, - SUSY skript, http://iktp.tu-dresden.de/Lehre/SS2010/SUSY/inhalt/SUSYSkript2010.pdf • Drees, Godbole, Roy - "Theory and Phenomenology of Sparticles" - World Scientific, 2004 • Baer, Tata - "Weak Scale Supersymmetry" - Cambridge University Press, 2006 • Aitchison - "Supersymmetry in Particle Physics. An Elementary Introduction" Institute of Physics Publishing, Bristol and Philadelphia, 2007 • Martin -"A Supersymmetry Primer" hep-ph/9709356 http://zippy.physics.niu.edu/primer.html If I use “then” more than once please shoot me! The lectures will cover material necessary to give a reasonable understanding of SUSY and realistic supersymmetric models which might be detected at the LHC as well as prepare the audience to do SUSY phenomenology. Starting with the SUSY algebra for N=1 supersymmetry we will then introduce superfields (general, chiral and vector) which will then aid us in constructing a SUSY invariant Lagrangian. We will then discuss how supersymmetry can be broken softly to provide realistic models which still solve the Hierarchy problem. We will then use all of this to construct the Minimal Supersymmetric Standard Model (MSSM) and then discuss how electroweak symmetry breaking works there and how the gauge eigenstates are mixed to form mass eigenstates. Finally I will talk about a few topics which go beyond the standard scenarios. 1 SUSY Algerbra 1.1 Poincare Algebra Lorentz Trasnformation Rotations and Boosts from Special Relativity scalar product invariant Translations Poincare Transformations Infinitesimal: ) 6 Independent entries in ) Lorentz group : 3 rotations + 3 boosts Poincare group : 4 translations + 6 Lorentz Representation: Transforms the fields via 10 generators Infinitesimal: 4 generators of translation: 6 Lorentz generators: Commutation relations For example, a scalar: One representaion of the Poincare group Generators for a scalar field Must obey the general commutation relations for Poincare generators. Commutation relations Generators for a scalar field Exercise for the enthusiastic: check explicit form of generators satisfy general commutation relations For example orbital angular momentum is included: A Lorentz scalar only has integer valued angular momentum but fermions also have 1/2 integer spin in addition to orbital angular momentum. Need Spin operator Fulfills Poincare conditions for Fermions have spinor representation of Lorentz group, with transformation: Generators for a spinor Coleman-Mandula “No-go theorem” [Coleman, Mandula Phys. Rev. 159, 1251 (1967).] [Stated here, without proof] A Lie group containing the Poincare group and an internal group, e.g. the Standard Model gauge group, will be formed by the direct product: Space-time internal Extending with a new group with space time which has generators that don’t commute is impossible. This does not exclude a symmetry with fermionic generators! [Gol’fand Y A and Likhtman E P 1971 JETP Lett. 13 323] Haag, Lopuszanski and Sohnius extension: SUSY algebra! [Haag R, Lopusanski J T and Sohnius M 1975 Nucl. Phys. B 88 257] Supersymmetry is the only way to extend space-time symmetries! Notational interlude Note: In these lectures we will use the Weyl representation of the clifford algebra. For example: Z-component of spin 1.2 SUSY Algebra (N=1) From the Haag, Lopuszanski and Sohnius extension of the Coleman-Mandula theorem we need to introduce fermionic operators as part of a “graded Lie algebra” or “superalgerba” introduce spinor operators and Weyl representation: Note Q is Majorana Weyl representation: Immediate consequences of SUSY algebra: SUSY charges are spinors that carries ½ integer spin. Weyl representation: Immediate consequences of SUSY algebra: ) superpartners must have the same mass (unless SUSY is broken). Non-observation ) SUSY breaking (much) Later we will see how superpartner masses are split by (soft) SUSY breaking Weyl representation: Immediate consequences of SUSY algebra: OR SUSY breaking requires Notes: 1. Since Q is a spinor it carries ½ integer spin. 2. [P^2, Q] = 0 ) superpartners must have the same mass (unless SUSY is broken). 3. From anti-commutation relation Hamiltonian is +ve definite If SUSY is respected by the vacuum then If SUSY is broken then 4. Local SUSY ! supergravitation, superstrings , Quantum theory of gravity. (beyond scope of current lectures) 1.3 First Look at supermultiplets SUSY chiral supermultiplet with electron + selectron: Try simple case (not general solution) for illustration Take an electron, with m= 0 (good approximation): 4 states: Just need 2 states: Electric charge = conserved quantity from internal U(1) symmetry that commutes with space-time symmetries, ) SUSY transformations can’t change charge. We have the states: We can also examine the spins of these states using the SUSY algebra Extension of electron to SUSY theory, 2 superpartners with spin 0 to electron states Electron spin 0 superpartners dubbed ‘selectrons’