fundamentals of linear algebra
... prime fields Fp as examples that will be used later on. We then introduce the notion of an abstract vector space over an arbitrary field and discuss ...
... prime fields Fp as examples that will be used later on. We then introduce the notion of an abstract vector space over an arbitrary field and discuss ...
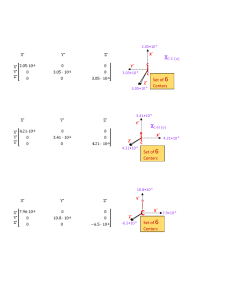
Galois Field Computations A Galois field is an algebraic field that
... For background information about Galois fields or their use in error-control coding, see the works listed in Selected Bibliography for Galois Fields. For more details about specific functions that process arrays of Galois field elements, see the online reference entries in the documentation for MATL ...
... For background information about Galois fields or their use in error-control coding, see the works listed in Selected Bibliography for Galois Fields. For more details about specific functions that process arrays of Galois field elements, see the online reference entries in the documentation for MATL ...
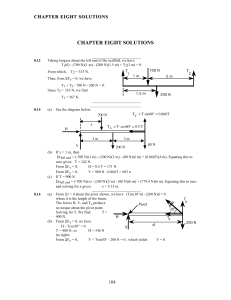
Phy CH 06 momentum - Milton-Union Exempted Village Schools
... because the bowling ball has more momentum than the playground ball does. When we think of a massive object moving at a high velocity, we often say that the object has a large momentum. A less massive object with the same velocity has a smaller momentum. On the other hand, a small object moving with ...
... because the bowling ball has more momentum than the playground ball does. When we think of a massive object moving at a high velocity, we often say that the object has a large momentum. A less massive object with the same velocity has a smaller momentum. On the other hand, a small object moving with ...
PDF of Version 2.01-B of GIAA here.
... (The “number system” referred to is the set of 2×2 matrices whose entries are real numbers.) When you read a sentence such as this, the first thing that you should do is verify the computation yourselves. Mathematical insight comes from mathematical experience, and you cannot expect to gain mathemat ...
... (The “number system” referred to is the set of 2×2 matrices whose entries are real numbers.) When you read a sentence such as this, the first thing that you should do is verify the computation yourselves. Mathematical insight comes from mathematical experience, and you cannot expect to gain mathemat ...