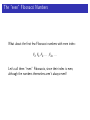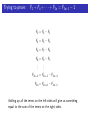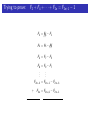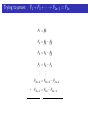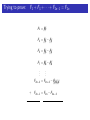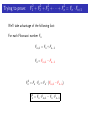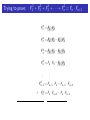Download The Fibonacci Numbers

The Fibonacci Numbers
The numbers are:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, . . .
Each Fibonacci number is the sum of the previous two Fibonacci
numbers!
Let n any positive integer. If Fn is what we use to describe the nth
Fibonacci number, then
Fn = Fn−1 + Fn−2
Trying to prove:
F1 + F2 + · · · + Fn = Fn+2 − 1
We proved a theorem about the sum of the first few Fibonacci
numbers:
Theorem
For any positive integer n, the Fibonacci numbers satisfy:
F1 + F2 + F3 + · · · + Fn = Fn+2 − 1
The “even” Fibonacci Numbers
What about the first few Fibonacci numbers with even index:
F2 , F4 , F6 , . . . , F2n , . . .
Let’s call them “even” Fibonaccis, since their index is even,
although the numbers themselves aren’t always even!!
The “even” Fibonacci Numbers
Some notation: The first “even” Fibonacci number is F2 = 1.
The second “even” Fibonacci number is F4 = 3.
The third “even” Fibonacci number is F6 = 8.
The tenth “even” Fibonacci number is F20 =??.
The nth “even” Fibonacci number is F2n .
HOMEWORK
Tonight, try to come up with a formula for the sum of the first few
“even” Fibonacci numbers.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, . . .
Let’s look at the first few:
F2 + F4 = 1 + 3 = 4
F2 + F4 + F6 = 1 + 3 + 8 = 12
F2 + F4 + F6 + F8 = 1 + 3 + 8 + 21 = 33
F2 + F4 + F6 + F8 + F10 = 1 + 3 + 8 + 21 + 55 = 88
See a pattern?
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, . . .
It looks like the sum of the first few “even” Fibonacci numbers is
one less than another Fibonacci number.
But which one?
F2 + F4 = 1 + 3 = 4 = F5 − 1
F2 + F4 + F6 = 1 + 3 + 8 = 12 = F7 − 1
F2 + F4 + F6 + F8 = 1 + 3 + 8 + 21 = 33 = F9 − 1
F2 + F4 + F6 + F8 + F10 = 1 + 3 + 8 + 21 + 55 = 88 = F11 − 1
Can we come up with a formula for the sum of the first few “even”
Fibonacci numbers?
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, . . .
Let’s look at the last one we figured out:
F2 + F4 + F6 + F8 + F10 = 1 + 3 + 8 + 21 + 55 = 88 = F11 − 1
The sum of the first 5 even Fibonacci numbers (up to F10 ) is the
11th Fibonacci number less one.
Maybe it’s true that the sum of the first n “even” Fibonacci’s is
one less than the next Fibonacci number. That is,
Conjecture
For any positive integer n, the Fibonacci numbers satisfy:
F2 + F4 + F6 + · · · + F2n = F2n+1 − 1
Trying to prove:
F2 + F4 + · · · F2n = F2n+1 − 1
Let’s try to prove this!!
We’re trying to find out what
F2 + F4 + · · · F2n
is equal to.
Well, let’s proceed like the last theorem.
Trying to prove:
F2 + F4 + · · · F2n = F2n+1 − 1
We know F3 = F2 + F1 .
So, rewriting this a little:
F2 = F3 − F1
Also: we know F5 = F4 + F3 .
So:
F4 = F5 − F3
In general:
Feven = Fnext odd − Fprevious odd
Let’s put these together:
Trying to prove:
F2 + F4 + · · · + F2n = F2n+1 − 1
F2 = F3 − F1
F4 = F5 − F3
F6 = F7 − F5
F8 = F9 − F7
..
..
.
.
F2n−2 = F2n−1 − F2n−3
F2n = F2n+1 − F2n−1
Adding up all the terms on the left sides will give us something
equal to the sum of the terms on the right sides.
Trying to prove:
F2 + F4 + · · · + F2n = F2n+1 − 1
F2 = /F//3 − F1
F4 = F5 − /F//3
F6 = F7 − F5
F8 = F9 − F7
..
..
.
.
F2n−2 = F2n−1 − F2n−3
+ F2n = F2n+1 − F2n−1
Trying to prove:
F2 + F4 + · · · + F2n = F2n+1 − 1
F2 = /F//3 − F1
F4 = /F//5 − /F//3
F6 = F7 − /F//5
F8 = F9 − F7
..
..
.
.
F2n−2 = F2n−1 − F2n−3
+ F2n = F2n+1 − F2n−1
Trying to prove:
F2 + F4 + · · · + F2n = F2n+1 − 1
F2 = /F//3 − F1
F4 = /F//5 − /F//3
F6 = /F//7 − /F//5
F8 = F9 − /F//7
..
.
..
.
F2n−2 = F2n−1 − F2n−3
+ F2n = F2n+1 − F2n−1
Trying to prove:
F2 + F4 + · · · + F2n = F2n+1 − 1
F2 = /F//3 − F1
F4 = /F//5 − /F//3
F6 = /F//7 − /F//5
F8 = /F//9 − /F//7
..
.
..
.
F2n−2 = F2n−1 − /F//2n−3
/////
+ F2n = F2n+1 − F2n−1
Trying to prove:
F2 + F4 + · · · + F2n = F2n+1 − 1
F2 = /F//3 − F1
F4 = /F//5 − /F//3
F6 = /F//7 − /F//5
F8 = /F//9 − /F//7
..
.
..
.
F2n−2 = /F//2n−1
///// − /F//2n−3
/////
+ F2n = F2n+1 − /F//2n−1
/////
Trying to prove:
F2 + F4 + · · · + F2n = F2n+1 − 1
F2 = /F//3 − F1
F4 = /F//5 − /F//3
F6 = /F//7 − /F//5
F8 = /F//9 − /F//7
..
.
..
.
F2n−3
F2n−2 = /F//2n−1
///// − ////////
+ F2n = F2n+1 − ////////
F2n−1
F2 + F4 + F6 + · · · + F2n = F2n+1 − F1
Trying to prove:
F2 + F4 + · · · + F2n = F2n+1 − 1
F2 = /F//3 − F1
F4 = /F//5 − /F//3
F6 = /F//7 − /F//5
F8 = /F//9 − /F//7
..
.
..
.
F2n−3
F2n−2 = /F//2n−1
///// − ////////
+ F2n = F2n+1 − ////////
F2n−1
F2 + F4 + F6 + · · · + F2n = F2n+1 − 1
Trying to prove:
F2 + F4 + · · · F2n = F2n+1 − 1
This proves our second theorem!!
Theorem
For any positive integer n, the even Fibonacci numbers satisfy:
F2 + F4 + F6 + · · · + F2n = F2n+1 − 1
The “odd” Fibonacci Numbers
What about the first few Fibonacci numbers with odd index:
F1 , F3 , F5 , . . . , F2n−1 , . . .
Let’s call them “odd” Fibonaccis, since their index is odd,
although the numbers themselves aren’t always odd!!
The “odd” Fibonacci Numbers
Some notation: The first “odd” Fibonacci number is F1 = 1.
The second “odd” Fibonacci number is F3 = 2.
The third “odd” Fibonacci number is F5 = 5.
The tenth “odd” Fibonacci number is F19 =??.
The nth “odd” Fibonacci number is F2n−1 .
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, . . .
Let’s look at the first few:
F1 + F3 = 1 + 2 = 3
F1 + F3 + F5 = 1 + 2 + 5 = 8
F1 + F3 + F5 + F7 = 1 + 2 + 5 + 13 = 21
F1 + F3 + F5 + F7 + F9 = 1 + 2 + 5 + 13 + 34 = 55
See a pattern?
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, . . .
It looks like the sum of the first few “odd” Fibonacci numbers is
another Fibonacci number.
But which one?
F1 + F3 = 1 + 2 = 3 = F4
F1 + F3 + F5 = 1 + 2 + 5 = 8 = F6
F1 + F3 + F5 + F7 = 1 + 2 + 5 + 13 = 21 = F8
F1 + F3 + F5 + F7 + F9 = 1 + 2 + 5 + 13 + 34 = 55 = F10
Can we come up with a formula for the sum of the first few “even”
Fibonacci numbers?
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, . . .
Maybe it’s true that the sum of the first n “odd” Fibonacci’s is the
next Fibonacci number. That is,
Conjecture
For any positive integer n, the Fibonacci numbers satisfy:
F1 + F3 + F5 + · · · + F2n−1 = F2n
F1 + F3 + · · · + F2n−1 = F2n
Trying to prove:
Let’s try to prove this!!
We know F2 = F1 .
So, rewriting this a little:
F1 = F2
Also: we know F4 = F3 + F2 .
So:
F3 = F4 − F2
In general:
Fodd = Fnext even − Fprevious even
Trying to prove:
F1 + F3 + · · · + F2n−1 = F2n
F1 = F2
F3 = F4 − F2
F5 = F6 − F4
F7 = F8 − F6
..
..
.
.
F2n−3 = F2n−2 − F2n−4
+
F2n−1 = F2n − F2n−2
Adding up all the terms on the left sides will give us something
equal to the sum of the terms on the right sides.
Trying to prove:
F1 + F3 + · · · + F2n−1 = F2n
F1 = /F//2
F3 = F4 − /F//2
F5 = F6 − F4
F7 = F8 − F6
..
..
.
.
F2n−3 = F2n−2 − F2n−4
+ F2n−1 = F2n − F2n−2
Trying to prove:
F1 + F3 + · · · + F2n−1 = F2n
F1 = /F//2
F3 = /F//4 − /F//2
F5 = F6 − /F//4
F7 = F8 − F6
..
..
.
.
F2n−3 = F2n−2 − F2n−4
+ F2n−1 = F2n − F2n−2
Trying to prove:
F1 + F3 + · · · + F2n−1 = F2n
F1 = /F//2
F3 = /F//4 − /F//2
F5 = /F//6 − /F//4
F7 = F8 − /F//6
..
.
..
.
F2n−3 = F2n−2 − F2n−4
+ F2n−1 = F2n − F2n−2
Trying to prove:
F1 + F3 + · · · + F2n−1 = F2n
F1 = /F//2
F3 = /F//4 − /F//2
F5 = /F//6 − /F//4
F7 = /F//8 − /F//6
..
.
..
.
F2n−3 = F2n−2 − /F//2n−4
/////
+ F2n−1 = F2n − F2n−2
Trying to prove:
F1 + F3 + · · · + F2n−1 = F2n
F1 = /F//2
F3 = /F//4 − /F//2
F5 = /F//6 − /F//4
F7 = /F//8 − /F//6
..
.
..
.
F2n−4
F2n−3 = /F//2n−2
//
///// − //////
+ F2n−1 = F2n − /F//2n−2
/////
F1 + F3 + · · · + F2n−1 = F2n
Trying to prove:
F1 + F3 + · · · + F2n−1 = F2n
This proves our third theorem!!
Theorem
For any positive integer n, the Fibonacci numbers satisfy:
F1 + F3 + F5 + · · · + F2n−1 = F2n
So far:
Theorem (Sum of first few Fibonacci numbers.)
For any positive integer n, the Fibonacci numbers satisfy:
F1 + F2 + F3 + · · · + Fn = Fn+2 − 1
Theorem (Sum of first few EVEN Fibonacci numbers.)
For any positive integer n, the Fibonacci numbers satisfy:
F2 + F4 + F6 + · · · + F2n = F2n+1 − 1
Theorem (Sum of first few ODD Fibonacci numbers.)
For any positive integer n, the Fibonacci numbers satisfy:
F1 + F3 + F5 + · · · + F2n−1 = F2n
One more theorem about sums:
Theorem (Sum of first few SQUARES of Fibonacci numbers.)
For any positive integer n, the Fibonacci numbers satisfy:
F12 + F22 + F32 + · · · + Fn2 = Fn · Fn+1
Trying to prove:
F12 + F22 + F32 + · · · + Fn2 = Fn · Fn+1
We’ll take advantage of the following fact:
For each Fibonacci number Fn
Fn+1 = Fn + Fn−1
Fn = Fn+1 − Fn−1
Fn2 = Fn · Fn = Fn · (Fn+1 − Fn−1 )
Fn2 = Fn · Fn+1 − Fn · Fn−1
Trying to prove:
F12 + F22 + F32 + · · · + Fn2 = Fn · Fn+1
Let’s check this formula for a few different valus of n:
Fn2 = Fn · Fn+1 − Fn · Fn−1
n = 4:
F42 = F4 · F4+1 − F4 · F4−1
F42 = F4 · F5 − F4 · F3
32 = 3 · 5 − 3 · 2
9 = 15 − 6
It works for n = 4!
Trying to prove:
F12 + F22 + F32 + · · · + Fn2 = Fn · Fn+1
Let’s check this formula for a few different valus of n:
Fn2 = Fn · Fn+1 − Fn · Fn−1
n = 8:
F82 = F8 · F8+1 − F8 · F8−1
F82 = F8 · F9 − F8 · F7
212 = 21 · 34 − 21 · 13
441 = 714 − 273 = 441
It works for n = 8!
Trying to prove:
F12 + F22 + F32 + · · · + Fn2 = Fn · Fn+1
Let’s use this formula:
Fn2 = Fn · Fn+1 − Fn · Fn−1
To find out what the sum of the first few SQUARES of Fibonacci
numbers is:
F12 + F22 + F32 + · · · + Fn2 =????
Trying to prove:
F12 + F22 + F32 + · · · + Fn2 = Fn · Fn+1
We’re using:
Fn2 = Fn · Fn+1 − Fn · Fn−1
F12 = F1 · F2
F22 = F2 · F3 − F2 · F1
F32 = F3 · F4 − F3 · F2
F42 = F4 · F5 − F4 · F3
..
.
..
.
2
Fn−1
= Fn−1 · Fn − Fn−1 · Fn−2
+
Fn2 = Fn · Fn+1 − Fn · Fn−1
Trying to prove:
F12 + F22 + F32 + · · · + Fn2 = Fn · Fn+1
F12 = /F//1//·//F/2/
F22 = F2 · F3 − ////////
F2 · F1/
F32 = F3 · F4 − F3 · F2
F42 = F4 · F5 − F4 · F3
..
.
..
.
2
Fn−1
= Fn−1 · Fn − Fn−1 · Fn−2
+ Fn2 = Fn · Fn+1 − Fn · Fn−1
Trying to prove:
F12 + F22 + F32 + · · · + Fn2 = Fn · Fn+1
F12 = /F//1//·//F/2/
F22 = /F//2//·//F/3/ − ////////
F2 · F1/
F32 = F3 · F4 − ////////
F3 · F2/
F42 = F4 · F5 − F4 · F3
..
.
..
.
2
Fn−1
= Fn−1 · Fn − Fn−1 · Fn−2
+ Fn2 = Fn · Fn+1 − Fn · Fn−1
Trying to prove:
F12 + F22 + F32 + · · · + Fn2 = Fn · Fn+1
F12 = /F//1//·//F/2/
F22 = /F//2//·//F/3/ − ////////
F2 · F1/
F32 = /F//3//·//F/4/ − ////////
F3 · F2/
F4 · F3/
F42 = F4 · F5 − ////////
..
.
..
.
2
Fn−1
= Fn−1 · Fn − Fn−1 · Fn−2
+ Fn2 = Fn · Fn+1 − Fn · Fn−1
Trying to prove:
F12 + F22 + F32 + · · · + Fn2 = Fn · Fn+1
F12 = /F//1//·//F/2/
F22 = /F//2//·//F/3/ − ////////
F2 · F1/
F32 = /F//3//·//F/4/ − ////////
F3 · F2/
F42 = /F//4//·//F/5/ − ////////
F4 · F3/
..
.
..
.
2
Fn−1
= Fn−1 · Fn − F
· Fn−2
n−1
////
///////////
+ Fn2 = Fn · Fn+1 − Fn · Fn−1
Trying to prove:
F12 + F22 + F32 + · · · + Fn2 = Fn · Fn+1
F12 = /F//1//·//F/2/
F22 = /F//2//·//F/3/ − /F////////
2 · F1
F32 = /F//3//·//F/4/ − /F////////
3 · F2
F42 = /F//4//·//F/5/ − /F////////
4 · F3
..
.
..
.
2
Fn−1
=F
n−1 · Fn−2
//n−1
//////·//F/n+1
//// − F
//////////////
/
+ Fn2 = Fn · Fn+1 − ////////////
Fn · Fn−1
F12 + F22 + F32 + · · · + Fn2 = Fn · Fn+1
Our fourth theorem:
Theorem (Sum of first few SQUARES of Fibonacci numbers.)
For any positive integer n, the Fibonacci numbers satisfy:
F12 + F22 + F32 + · · · + Fn2 = Fn · Fn+1
So far:
Theorem (Sum of first few Fibonacci numbers.)
F1 + F2 + F3 + · · · + Fn = Fn+2 − 1
Theorem (Sum of first few EVEN Fibonacci numbers.)
F2 + F4 + F6 + · · · + F2n = F2n+1 − 1
Theorem (Sum of first few ODD Fibonacci numbers.)
F1 + F3 + F5 + · · · + F2n−1 = F2n
Theorem (Sum of first few SQUARES of Fibonacci numbers.)
F12 + F22 + F32 + · · · + Fn2 = Fn · Fn+1
Examples
1 + 2 + 5 + 13 + 34 + 89 + 233 + 610 + 1597 + 4181 = 6765
1+1+4+9+25+64+169+441+1156+3025+7921 = 89·144 = 12816
Now, complete this worksheet .....