Download 01-24 3.1-3.2 Adding/Subtracting Whole Numbers

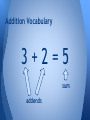
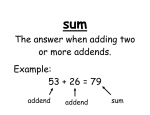
§3.1 Adding Whole
Numbers
1/20/17
Today We’ll Discuss
What are the properties of addition for
whole numbers?
How do we use models to add whole
numbers?
How do we use algorithms to add whole
numbers?
The Set Model
The most basic way we teach students
about the concept of addition is using the
idea of “putting together.”
In terms of sets, this is the union of A and
B, written as A∪B.
Definition: The union of two sets A,B is the
set of everything either in A OR B.
The Set Model
The set model uses the idea that the
cardinality of the union of two sets is the
sum of the cardinalities of the original sets.
(Assume that A and B do not have any of
the same elements between them!)
Addition Vocabulary
3+2=5
sum
addends
Memorization!
Properties of Addition
Commutative Property of Addition
The sum of two numbers does not depend
on the order of the addends.
Associative Property of Addition
The sum of numbers does not depend on
the grouping of the addends.
Additive Identity Property
The sum of any number with the additive
identity 0 is the original number.
Example
Identify the property of addition that
makes each equation true.
1) 2 + x = x + 2
2) 5 + 0 = 5
3) (2 + 9) + 1 = 2 + (9 + 1) = 2 + 9 + 1
Number Line Model
For small whole numbers, students can
count the combined distance from zero on
a number line to complete an addition
problem. Always Start at zero!
Example
Use a number line to explain to a student
how to add
3+5
Example
Use a number line to explain the
commutative property of addition to a
student.
Base-Ten Block Model
For larger whole numbers, we begin
introducing students to keeping track of
place values and regrouping.
Standard / Traditional Algorithm
At least when I was in school, I was taught
to add by regrouping manually, using the
standard algorithm.
1
34
+ 27
61
Add in each place
value, starting with
ones. Regroup
mentally while adding.
Expanded Algorithm
You can avoid the mental math and
“carrying the one” by completing the
addition using the expanded algorithm.
34
+ 27
11
+ 50
61
Add in each place
value, starting with
ones. Write each place
value sum. Add again.
Examples
a) 46 + 85
b) 237 + 669
c) 1894 + 234
Example
You work as a park ranger and are counting
the numbers of sea turtle nests along five
different stretches of a beach. Your counts
are 147, 204, 158, 324, and 92. What is the
total number of nests along the five
stretches of beach?
§3.2 Subtracting Whole
Numbers
1/24/17
Today We’ll Discuss
What is the definition of the difference of
two whole numbers?
How do we use models to subtract whole
numbers?
How do we use algorithms to subtract
whole numbers?
Warning!
Subtraction is not commutative!
9 – 5 is not the same as 5-9
One is the “difference of 9 and 5” and the
other is the “difference of 5 and 9”
Subtraction is not associative!
Also (5 – 3) – 2 = 0 but 5 – (3-2) = 1
Inverse Operations
A theme of mathematics is asking, “what
can I do to undo an operation?”
Subtraction is the inverse operation of
addition because it will “undo” the
addition.
Likewise, addition is the inverse operation
of subtraction.
What is Subtraction?
Given two numbers a and b such that a ≥ b,
what is the difference of a and b?
That is, what is
a−b?
Missing Addend Method
(Guess and Check)
The difference a − b can be thought of as
the whole number such that
b + (a − b) = a
Subtrahend
Missing
addend
Minuend
Missing Addend Method
(Guess and Check)
The difference a − b can be thought of as
the whole number such that
b + (a − b) = a
Subtrahend
Difference
Minuend
Missing Addend Method
(Guess and Check)
The difference a − b can be thought of as
the whole number such that
8−5=3
Minuend
Subtrahend
Difference
Example
Use the missing addend method to find
each difference:
a) 9 − 5
b) 10 − 3
Example
Use the missing addend method to find
each difference:
a) 5 +
=9
b) 3 +
= 10
Take-Away Method
5−2=3
Number Line Model
Minuend
Subtrahend
Example
Use a number line to find 10 − 3.
Base-Ten Blocks
We again use base-ten blocks, this time to
introduce the idea of “breaking up” or
“taking away.”
We begin with the minuend, and then
remove the subtrahend.
57
57 − 23
34
Example
Use base-ten blocks to find each
difference.
a) 345 − 242
b) 113 − 96
c) 90 − 33
d) 105 − 54
Standard Algorithm
The standard algorithm is what most of us
grew up with.
5
1
61
- 34
27
Subtract in each place
value. If not enough in
that position, regroup,
move a “1”, and
record the removal.
Austrian Algorithm
The Austrian algorithm, at least according
to our book, is used more in Europe.
61
- 34
27
1
Subtract in each place
value. If not enough in
that position, place a
“1” between the
relevant columns...
Example
Use the Austrian algorithm to find the
following differences.
a) 83 − 56
b) 331 − 172
c) 7132 − 4568
Example
You write a check to buy some clothes.
After subtracting the amount from your
account, your balance does not seem
correct. What is the correct balance?
Homework #4
§3.1 Pages 82-85
#5,8,16,22,24
§3.2 Pages 92-95
#6,8,14,22,24
Due: 1/26/17