Download supplementary material

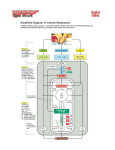
SUPPLEMENTARY MATERIAL
1. Assays of the activities of the mitochondrial respiratory chain complexes. Complex I
(rotenone-sensitive NADH dehydrogenase) activity was assayed at 340 nm using the electron acceptor
2,3-dimethoxy-5-methyl-6-n-decyl-1,4-benzoquinone (0.1 mM) and 0.25 mM NADH as electron
donor, in the presence of 1 mM KCN. The addition of 5 M rotenone allowed us to determine the
rotenone-sensitive activity. A total of 50-100 g mitochondrial protein was used for each
measurement. Complex II (Succinate dehydrogenase) activity was measured at 600 nm using 80 M
2,6-dichloroindophenol as electron acceptor and 15 mM succinate as donor in the presence of 1 mM
KCN. The addition of 15 mM malonate completely inhibited the oxidation of succinate. Complex I/III
(NADH cytochrome-c reductase) activity was measured at 340 nm using 50 M cytochrome c3+ as
acceptor and 0.25 mM NADH as donor in the presence of 1 mM KCN. Either 5 M rotenone
(Complex I inhibitor) or 1 M antimycin A (Complex III inhibitor) was added subsequently to the
reaction mixture. Complex II/III (Succinate cytochrome-c reductase) assay was performed at 550 nm
using 50 M cytochrome c3+ as acceptor and 15 mM succinate as donor in the presence of 1 mM
KCN. Either 15 mM malonate (Complex II inhibitor) or 1 M antimycin A (Complex III inhibitor)
was added subsequently to the reaction mixture. Complex IV (Cytochrome-c oxidase) activity was
determined at 550 nm using 50 M reduced cytochrome c2+ as donor. The subsequent addition of 1
mM KCN (Complex IV inhibitor) enabled us to quantify the complex activity. The GLUDH activity
assay was performed at 340 nm in Tris buffer (100 mM Tris, pH 8.0). The reaction mixture contained
0.25 mM NADH, 10 mM NH4Cl and 2 mM MgADP as an activator, and the reaction was initiated by
adding 2 mM alpha-ketoglutaric acid.
2. Determination of metabolite concentrations to follow fluxes. To two volumes of sample one
volume of ice cold 1.2 N HClO4 was added. After homogenization, samples were centrifuged at
15 000 g at 4°C for 10 minutes. To 10 volumes of supernatant 1 volume of 1 M triethanolamine was
added, and the sample was neutralized to pH 7.0 with 5 M K2CO3. The neutralized extract was kept in
an ice-bucket and after the potassium perchlorate precipitate had settled, the supernatant was used for
enzymatic determination of pyruvate and lactate. In all cases the NADH consumption/production was
followed spectrophotometrically at 340 nm. In the case of the pyruvate, the measurement was
performed in Tris buffer (100 mM Tris pH 8.0) containing 0.25 mM NADH and LDH as auxiliary
enzyme. For lactate measurement, the reaction mixture contained 1% hydrazine, 4 mM NAD+ and
LDH as auxiliary enzyme. The buffer was 0.2 M glycine of pH 9.6
3. Western Blot. Proteins were separated by SDS/PAGE (12% gel) and electrotransferred to
PVDF transfer membrane for 1-3 hour at 140 mA. The filters were subjected to immunoblotting with
antisera directed against huntingtin in rabbit or GAPDH in mouse. The huntingtin antibody was
directed against the first 17 amino acids of the N-terminal part of this protein, and it recognizes both
mutant and normal huntingtin. Antibody binding was revealed by using anti-rabbit IgG or anti-mouse
IgG, respectively, both coupled to peroxidase, and ECLTM Western Blotting Detection Reagents
(Amersham Biosciences).
4. Rate equations and kinetic parameters used for the simulation.
Enzyme-catalysed reactions:
vHK
Glucose + ATP → G6P + ADP
vGPI
G6P ↔ F6P
vPFK
F6P + ATP → FBP + ADP
vAldolase
FBP ↔ DHAP + GAP
v
GAP ↔ DHAP
vGAPDH
GAP + NAD+ + Pi ↔ BPG + NADH + H+
vPGK
GDP + ADP ↔ P3G + ATP
vPGM
P3G ↔ P2G
TPI
v
P2G ↔ PEP + H2O
vPK
PEP + ADP → Pyruvate + ATP
vLDH
Pyruvate + NADH ↔ Lactate + NAD+
vtr
Pyruvateintracellular → Pyruvateextracellular
Enolase
DHAP + NADH ↔ GP + NAD+, where GP is glycerol-3-phosphate.
GDH
v
Product insensitive Michaelis-Menten kinetics:
v
Vmax * S 
, where Vmax is the maximum rate of this reaction and K m is the Michaelis-Menten
K m  S 
constant for the substrate S. S = Glucose for HK and F6P for PFK. At the kinetic measurements the
initial ATP concentration was 2 mM, and its maximum consumption during the flux measurements
was less than 5%. In the case of HK, there is no product (G6P) inhibition due to the presence of
inorganic Pi in the assay buffer [1]. In the case of PFK, no product (FBP) inhibition was observed
under similar conditions [1].
Reversible Michaelis-Menten kinetics:
v
Vmax
Km
S
[ P]
Ke
, where Vmax is the maximum forward rate of this reaction; K mS and KmP
*
[S ]
[ P]
1

S
P
Km
Km
[S ] 
are the Michaelis-Menten constants for substrate S and product P, respectively; and Ke is the
equilibrium constant of this reaction. S = G6P and P = F6P for GPI; S = GAP and P = DHAP for TPI;
S = P3G and P = P2G for PGM, S = P2G and P = PEP for enolase.
Kinetic equations for a reversible reaction with two substrates and two products:
Vmax * ([ A] * B  
[ P] * [Q]
)
Ke
, where Vmax is
v
[ A]
[ B]
[ P]
[Q]
[ A] * [ B]
[ P] * [Q]
A
B
K m * K m * (1 





)
A
B
P
Q
A
B
P
Q
Km
Km
Km
Km
Km * Km
Km * Km
the maximum rate of this reaction; KmA, KmB, KmP and KmQ are the Michaelis-Menten constants for A,
B, P and Q, respectively; and Ke is the equilibrium constant of this reaction.
A = BPG, B = ADP, P = P3G, Q = ATP for PGK [2];
Vmax * ([ A] * B  
[ P] * [Q]
)
Ke
v
, where Vmax is the maximum rate of this
[ A] [ P]
[ B] [Q]
A
B
K m * K m * (1 

)  (1 

)
A
P
B
Q
Km
Km
Km
Km
reaction; KmA, KmB, KmP and KmQ are the Michaelis-Menten constants for A, B, P and Q, respectively;
and Ke is the equilibrium constant of this reaction.
A = GAP, B = NAD+, P = BPG, Q = NADH for GAPDH; A = DHAP, B = NADH, P = GP, Q =
NAD+ for GDH [3]; A = Pyruvate, B = NADH, P = Lactate, Q = NAD+ for LDH [4].
Kinetic equation for an irreversible reaction with two substrates (A and B) and two products:
v
Vmax * [ A] * B
( K m  [ A]) * ( K m  [ B])
A
B
, where Vmax is the maximum rate of this reaction; KmA and KmB are
the Michaelis-Menten constants for A and B, respectively. A = PEP, B = ADP for PK.
Kinetic equation for a reversible reaction with one substrate and two products:
[ P] * [Q]
)
Ke
, where Vmax is the maximum rate of this
v
[ A]
[ P]
[Q]
[ P] * [Q]
A
K m * (1 



)
A
P
Q
P
Q
Km
Km
Km
Km * Km
Vmax * ([ A] 
reaction; KmA, KmP and KmQ are the Michaelis-Menten constants for A, P and Q, respectively; and Ke
is the equilibrium constant of this reaction. A = FBP, P = DHAP, Q = GAP for aldolase.
HK
KmGlucose=
GPI
Hexokinase, EC 2.7.1.1
8 M [1].
Glucose-6-phosphate isomerase, EC 5.3.1.9
Vmax= 1670 mol/g/min, KmG6P= 392 M, KmF6P= 359 M, Ke= 0.327 [1].
PFK
Phosphofructokinase, EC 2.7.1.11
KmF6P= 15 M [1].
Aldolase
EC 4.1.2.13
KmFBP= 9 M [5], KmDHAP= 130 M, KmGAP= 300 M, Ke= 0.2 M.
TPI
Triosephosphate isomerase, EC 5.3.1.1
KmGAP= 650 M, KmDHAP= 1300 M, Ke= 9.
GAPDH
Glyceraldehyde-3-phosphate dehydrogenase, EC 1.2.1.12
KmGAP= 20 M [6], KmNAD+= 10 M, KmBPG= 12 M [6], KmNADH= 20 M, Ke= 400.
PGK
Phosphoglycerate kinase, EC 2.7.2.3
Vmax= 670 mol/g/min, KmBPG= 5 M, KmADP= 100 M [7], KmP3G= 200 M [7],
KmATP= 200 M [7], Ke= 10.
PGM
Phosphoglycerate mutase, EC 5.4.2.1
Vmax= 1670 mol/g/min, KmP3G= 200 M, KmP2G= 60 M, Ke= 0.17.
Enolase
EC 4.2.1.11
KmP2G= 46 M [8], KmPEP= 1000 M, Ke= 10.
PK
Pyruvate kinase, EC 2.7.1.40
KmPEP= 50 M [9], KmADP= 100 M.
Ki of ATP inhibition for PK is 2-10 mM (Brenda database http://www.brenda-enzymes.info/), which
does not result in significant changes in the PK activity (data not shown).
LDH
Lactate dehydrogenase, EC 1.1.1.27
KmPyruvate= 20 M, KmNADH= 20 M, KmLactate= 500 M, KmNAD+= 1000 M, Ke= 2500.
GDH
Glycerol-3-phosphate dehydrogenase, EC 1.1.1.8
KmDHAP= 20 M, KmNADH= 25 M [10], KmGP= 500 M [10], KmNAD+= 50 M [10], Ke= 200, where
GP is glycerol-3-phosphate.
Pyruvate transfer
vtr = ktr * [Pyr], ktr = 8 /min.
For the parameters where no data are available for mouse or rat brain, as indicated by the absence of a
reference, the values were estimated on the basis of the known parameters of different organisms taken
from the Brenda database (http://www.brenda-enzymes.info/).
For the simulation of conversion of glucose to lactate the initial concentrations of NAD +, glucose and
ATP were 3 mM, 2 mM and 2 mM, respectively. The protein concentration in the cuvette was 0.28
mg/ml. The following equations were used:
d[Glucose]/dt = - vHK, d[G6P]/dt = -vGPI + vHK, d[F6P]/dt = -vPFK + vGPI,
d[FBP]/dt = -vALD + vPFK, d[DHAP]/dt = -vGDH + vALD + vTPI,
d[GAP]/dt = -vGAPDH + vALD - vTPI, d[GDP]/dt = vGAPDH – vPGK ,
d[3-PG]/dt = -vPGM + vPGK , d[2-PG]/dt = vPGM – vEnolase , d[PEP]/dt = -vPK + vEnolase ,
d[Pyr]/dt = vPK– vLDH, d[Lac]/dt = vLDH, d[NAD+]/dt = -vGAPDH + vGDH + vLDH,
d[NADH]/dt = vGAPDH - vGDH - vLDH ,
d[ATP]/dt = vPK + vPGK - vHK - vPFK, d[ADP]/dt = -vPK - vPGK + vHK + vPFK,
d[GP]/dt = vGDH, where GP is glycerol-3-phosphate.
For the simulation of “quasi”-physiological circumstances 100-fold higher protein concentration (V max
values) was introduced into the model. The concentrations of NAD+ (1 mM), NADH (0.1 mM), ATP
(2 mM) and ADP (0.2 mM) were kept constant. The influx concentration of glucose was kept constant
(2 mM). Pyruvate can be transported through the cell membrane or to the mitochondria, therefore a
first-order reaction was introduced to model this transport process. The following equations were used:
d[Glucose]/dt = 0, d[G6P]/dt = -vGPI + vHK, d[F6P]/dt = -vPFK + vGPI,
d[FBP]/dt = -vALD + vPFK, d[DHAP]/dt = vALD + vTPI – vGDH,
d[GAP]/dt = -vGAPDH + vALD - vTPI, d[GDP]/dt = vGAPDH – vPGK ,
d[3-PG]/dt = -vPGM + vPGK , d[2-PG]/dt = vPGM – vEnolase , d[PEP]/dt = -vPK + vEnolase ,
d[Pyr]/dt = vPK– vtr, d[NAD+]/dt =0, d[NADH]/dt = 0, d[ATP]/dt = 0, d[ADP]/dt = 0,
d[GP]/dt = vGDH, where GP refers to glycerol-3-phosphate.
.
References
1. Orosz F, Wagner G, Ortega F, Cascante M & Ovadi J (2003) Glucose conversion by multiple
pathways in brain extract: theoretical and experimental analysis. Biochem Biophys Res Commun 309,
792-797.
2. Lee CS & O'Sullivan WJ (1975) Properties and mechanism of human erythrocyte phosphoglycerate
kinase. J Biol Chem 250, 1275-1281.
3. Berrada W, Naya A, Iddar A & Bourhim N (2002) Purification and characterization of cytosolic
glycerol-3-phosphate dehydrogenase from skeletal muscle of jerboa (Jaculus orientalis). Mol Cell
Biochem 231, 117-127.
4. Holbrook JJ, Liljas A, Steindel SJ & Rossman MG (1975) Enzymes. 3rd Ed. 11, pp. 191-292.
5. Kusakabe T, Motoki K & Hori K (1994) Human aldolase C: characterization of the recombinant
enzyme expressed in Escherichia coli. J Biochem 115, 1172-1177.
6. Ryzlak MT & Pietruszko R (1988) Heterogeneity of glyceraldehyde-3-phosphate dehydrogenase
from human brain. Biochim Biophys Acta 954, 309-324.
7. Lee CY (1982) 3-Phosphoglycerate kinase isozymes and genetic variants from mouse. Methods
Enzymol 90 Pt., 121-126.
8. Suzuki F, Umeda Y & Kato K (1980) Rat brain enolase isozymes. Purification of three forms of
enolase. J Biochem 87, 1587-1594.
9. Feksa LR, Cornelio A, Dutra-Filho CS, De Souza Wyse AT, Wajner M & Wannmacher CM (2004)
Inhibition of pyruvate kinase activity by cystine in brain cortex of rats. Brain Res 1012, 93-100.
10. McGinnis JF & de Vellis J (1974) Purification and characterization of rat brain glycerol phosphate
dehydrogenase. Biochim Biophys Acta 364, 17-27.