Download doc

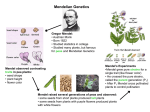
Chance Models in Mendel’s Genetics
Mendel’s theory shows the power of simple chance models in action. In 1865, Gregor Mendel published an
article which provided a scientific explanation for heredity, and eventually caused a revolution in biology. By a
curious twist of fortune, this paper was ignored for about thirty years, until the theory was simultaneously
rediscovered by three men, Correns in Germany, de Vries in Holland, and Tschermak in Australia. De Vries and
Tschermak are now thought to have seen Mendel’s paper before they published, but Correns apparently found
the idea by himself.
Mendels’ experiments were all carried out on garden peas; here is a brief account of one of these
experiments. Pea seeds are either yellow or green. (As the phrase suggests, seed color is a property of the seed
itself, and not of the parental plant: indeed, one parent often has seeds of both colors.) Mendel bred a pure yellow
strain, that is, a train in which every plant in every generation had only yellow seeds; and separately he bred a
pure green strain. He then crossed plants of the pure yellow strain with plants of the pure green strain: for
instance, he used pollen from the yellows to fertilize ovules on plants of the green strain. (The alternative method,
using pollen from the greens to fertilize plants of the yellow strain, gave exactly the same results.) The seeds
resulting from a yellow-green cross, and the plants into which they grow, are called “first generation hybrids.”
First generation hybrid seeds re all yellow, in distinguishable from seeds of the pure yellow strain. The green
seems to have disappeared completely.
These first-generation hybrid seeds grew into first-generation hybrid plants which Mendel crossed with
themselves, producing “second-generation hybrid” seeds. Some of these second-generation seeds were yellow,
but some were green. So the green disappeared for one generation, but reappeared in the second. Even more
surprising, the green reappeared in a definite simple proportion: of the second-generation hybrid seeds, about
75% were yellow and 25% were green.
What is behind this regularity? To explain it, Mendel postulated the existence of the entities now called
“genes.” According to Mendel’s theory, there were two different variants of a gene which paired up to control
seed color. They will be denoted here by y (for yellow) and g (for green). It is the gene-pair in the seed-not the
parent-which determines what the color the seed wil be, and all the cells making up a seed contain the same
gene-pair. There are four different gene-pairs: y/y, y/g, g/y, and g/g. Gene-pairs control seed color by the rule:
 y/y, y/g and g/y make yellow
 g/g makes green.
As geneticists say, y is “dominant” and g is “recessive.” This completes the first part of the model.
Now the seed grows up and becomes a plant; all cells in this plant also carry the seed’s color gene-pair —
with one exception. Sex cells, either sperm or eggs, contain only one gene of the pair. For instance, a plant whose
ordinary cells contain the gene-pair y/y will produce sperm cells each containing the gene y. On the other hand,
similarly, it will produce egg cells each containing the gene y. On the other hand, a plant whose ordinary cells
contain the gene-pair y/g will produce some sperm cells containing the gene y, and some sperm cells containing
the gene g. In fact, half its sperm cells will contain y, and the other half will contain g; similarly, half its eggs will
contain y, and the other half will contain g.
This model accounts for the experimental results. Plants of the pure yellow strain have the color gene-pair
y/y, so the sperm and eggs all just contain the gene y. Similarly, plants of the pure green strain have the gene-pair
g/g, so their pollen and ovules just contain the gene g. Crossing a pure yellow with a pure green amounts for
instance to fertilizing a g-egg by a y-sperm, producing a fertilized cell having the gene-pair y/g. This cell
produces itself and eventually becomes a seed, in which all the cells have the gene-pair y/g and are yellow in
color. The model has explained why all first-generation hybrid seeds are yellow, and none are green.
What about the second generation? A first-generation hybrid seeds grows into a first-generation hybrid plant,
with the gene-pair y/g. This plant produces sperm cell, of which half will contain gene y and the other half will
contain the gene g; it also produces eggs, of which half will contain y and the other half will contain g. When
two first-generation hybrids are crossed, each resulting second-generation hybrid seed gets one gene at random
from each parent—because it is formed by the random combination of a sperm cell and an egg.
Figure 1. Mendel’s chance model for the genetic determination of see-color: one gene is chosen
at random from parent. The chance of each combination is shown. (The sperm gene is listed first;
in terms of seed color, the combinations YG and GY are not distinguishable after fertilization.)
As shown in Figure 1, the seed has a 25% chance to get a gene-pair with two g’s and be green; it has a
75% chance to get a gene-pair with one or two y’s and be yellow. The number of seeds is small by
comparison with the number of pollen strains, so the selections for the various seeds are essentially
independent. The conclusion: the color of second-generation hybrid seeds will be determined as if by a
sequence of draws with replacement from the box
And that is how the model accounts for the reappearance of green in the second generation, for about 25%
of the seeds.
Mendel made a bold leap from his experimental evidence to his theoretical conclusions. His
reconstruction of the chain of heredity was based entirely on statistical evidence of the kind discussed here.
And he was right. Modern research in genetics and molecular biology is uncovering the chemical basis of
heredity, and has provided ample direct proof for the existence of Mendel’s hypothetical entities. As we
know today, genes are segments of DNA on chromosomes.
Essentially the same mechanism of heredity operates in all forms of life, from dolphins to fruit flies. So
the genetic model proposed by Mendel unlocks one of the great mysteries of life. How is it that pea-seed
always produces a pea, and never a tomato or a whale? Furthermore, the answer turns out to involve chance
in a crucial way, despite Einstein’s quote “I shall never believe that God plays dice with the world”.
An appreciation of the Mendel’s genetic model
Chance models are now used in many fields. Usually, the models only assert that certain entities behave as
if they were determined by drawing tickets at random from a box, and little effort is spent establishing a physical
basis for the claim of randomness. Indeed, the models seldom say explicitly what is like the box, or what is like
the tickets.
The genetic model is quite unusual, in that it answers such questions. There are two main sources of
randomness in the model:
1. the random allotment of chromosomes (one from each pair) to sex cells;
2. the random pairing of sex cells to produce fertilized egg.
Did Mendel’s facts fit his model?
Mendel’s discovery ranks as one of the greatest in science. Today, his theory is amply proved and
extremely powerful. But how good was his own experimental proof? Did Mendel’s data prove his theory? Only
too well, answered by R.A. Fisher. Mendel’s observed frequencies were uncomfortably close to is expected
frequencies, much closer than ordinary chance variability would permit.
In one experiment, for instance, Mendel obtained 8,023 second-generation hybrid seeds. He expected
1/4*8023=2006 of them to be green, and observed 2001, for a discrepancy of 5. According to his own chance
model, about 88% of the time, chance variation would cause a discrepancy between Mendel’s expectations and
his observations greater than the one he reported. By itself, this evidence is not very strong. The trouble is, every
one of Mendel’s experiments shows this kind of unusually close agreement between expectations and
observations. Using the  -test to pool the results, Fisher showed that the chance of agreement as close as the
2
reported by Mendel is about four in a hundred thousand.
The Chi-square test
This test helps to evaluate the deviation of observed values from expected values.
 2  sum of
(observed frequency-expected frequency)2
.
expected frequency
Degree of freedom = number of terms in  — one.
2
With independent experiments, the results can be pooled by adding up the separate chi-square-statistics; the
degrees of freedom add up too.
Example 1. One of Mendel’s breeding trials came out as follows.
For this data,  =0.5, the degree of freedom = 4 -1 =3, p-value = 8%, which is inconclusive, but points to
2
fudging. If we observe this kind of independent experiments 5 times with all similar chi-square values, then the
chi-square statistic for the pooled data will be around 2.5 with degree of freedom 15. Then the p-value is about
0.00013.
Mendelian Concepts
Every diploid organism has two copies of each genetic locus carried on pairs of autosomes (chromosomes
other than sex chromosomes). A locus is an identifiable region on a chromosome, and it may correspond to a
gene or to a physical marker such as a sequence-tagged site (STS). The two gene copies corresponding to a
particular locus in an organism may or may not be exactly identical. During meiosis, alleles corresponding to a
particular locus segregate, which means that one copy of any locus appears in any given gamete. In contrast, two
different genes on the same chromosome do not segregate unless recombination has occurred.
If two alleles at a given locus are identical in an individual, then that individual is said to be homozygous
for the genes at that locus. If the two alleles are different, then the individual is heterozygous with respect to the
genes at that locus. Sometimes the phenotype associated with a gene fails to appear because of the particular
constellation of other genes in that individual or particularly environmental circumstance. The probability that a
gene confers the phenotype associated with it is called its penetrance.