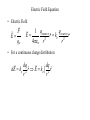Download PHYS_2326_012009

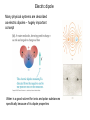
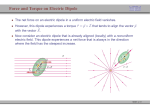
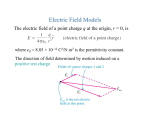
Forces and fields obey the
superposition principle:
Field from a group of
particles is a vector sum of
fields from each particle
E  E1  E 2  ...   Ei
i
E x  E1x  E2 x  ...   Eix
i
E y  E1 y  E2 y  ...   Eiy
i
E z  E1z  E2 z  ...   Eiz
i
Electric Field Properties
• A small positive test charge is used to determine the
electric field at a given point
• The electric field is a vector field that can be symbolized
by lines in space called electric field lines
• The electric field is continuous, existing at every point, it
just changes in magnitude with distance from the source
Electric Field Equation
• Electric Field

 F
E
qo

1 qsource
qsource
E
rˆ  ke 2 rˆ
2
4 o r
r
• For a continuous charge distribution


dq
dq
dE  ke 2 rˆ  E  ke  2 rˆ
r
r
For spatially distributed charges – we can sub-divide the object into the small,
“point-like” charges and integrate (sum up) the individual fields.
Often, we assign charge density for such spacious charged objects
 ...   ... dq
i
dq   dl  for lines (1  d )
dq   dA  for surfaces (2  d )
dq   dV  for volumes (3  d )
 ,  ,   correspond ing charge densities
 (r )
E.g. in 3 - d : E(r)  ke 
(r  r ) dV
3
| r - r |
x  x
E x ( x, y, z)  ke 
(x,y,z) dx dy dz
2
2
2 3/ 2
(( x  x)  ( y  y )  ( z  z ) )
Examples of field calculations: fields of continuous charge
distributions
Field of a ring of charge on the symmetry axis
Ex   dEx
E x   ke

dQ
dQ
cos


k
 e x2  a2
r2
E  Ex 
kQx
( x 2  a 2 )3/ 2
x
x2  a2
Positive charge is uniformly distributed
around a semicircle. The electric field
that this charge produces at the center of
curvature P is in
A. the +x-direction.
B. the –x-direction.
C. the +y-direction.
D. the –y-direction.
E. none of the above
Field of a disk, uniformly charged on the symmetry axis
Surface charge density is , radius R
Area dA of a ring of radius r
dA  2 rdr; 
R
rdr
E x  2 ke x  2 2 3/ 2
(x  r )
0
E x  2 ke x
x2  R2

x2
x2  r2  z
dz  2rdr
dz
 1  x 2  R2
 2 ke x 
 |x 2
3/ 2
z
 z
dQ
; dQ  2 r dr
dA
Changing variable of integration

 
x
Ex 
1 

2
2
2 0 
R  x 
For the limit of x<<R, we have an electric field of the infinite
plane sheet of charge and it is independent of the distance from
the plane (assuming that distance x<<linear dimensions of the sheet)

E plane 
2 0
Electric Field Line Properties
• Relation between field lines and electric field vectors:
a. The direction of the tangent to a field line is the direction of
the electric field E at that point
b. The number of field lines per unit area is proportional to the
magnitude of E: the more field lines the stronger E
• Electric field lines point in direction of force on a positive test
charge therefore away from a positive charge and toward a
negative charge
• Electric field lines begin on positive charges and end on negative
charges or infinity
• No two electric field lines can cross
Electric field lines
E is tangent to the electric field line – no 2 lines can
cross (E is unique at each point)
Magnitude of E is proportional to the density of the
lines
Remember, electric field lines are NOT trajectories!
When a particle moves on a curved path, the direction of
acceleration (and hence of the force) is not collinear with the
tangent to the curve
Electric dipole
Many physical systems are described
as electric dipoles – hugely important
concept
Water is a good solvent for ionic and polar substances
specifically because of its dipole properties
Torque on the electric dipole
r
r
p  qd
(electric dipole moment from “-” to “+”)
Electric field is uniform in space
Net Force is zero
 Torque is not zero
Net
  (qE )(d sin  )



  p E
(torque is a vector)
Stable and unstable equilibrium




p  E
p  E
Charge #2
Three point charges lie at the vertices of an
equilateral triangle as shown. Charges #2
and #3 make up an electric dipole.
The net electric torque that Charge #1 exerts
on the dipole is
+q
Charge #1
+q
y
–q
x
A. clockwise.
B. counterclockwise.
C. zero.
D. not enough information given to decide
Charge #3
Electric field of a dipole
E-field on the line connecting two charges
 1 1 
E  keq 2  2 
r2 r1 

-
A
+
E
r2
d
2 p ke
E 3
r

r1


E-field on the line perpendicular to the dipole’s axis
E  2E 2 sin

E2

E


2
 E2
d
r
E 2  ke
A
E1
-
q
r2
qd
E  ke 3
r
r
r
p
E  k e 3
r

when r>>d
+
d
General case – combination of the above two

 

3( p r )  p
E
r 3
5
r
r
Dipole’s Potential Energy
E-field does work on the dipole – changes its potential energy
Work done by the field (remember your mechanics class?)
dW   d   pE sin d
 
U p E
Dipole aligns itself to minimize its potential energy
in the external E-field.
Net force is not necessarily zero in the non-uniform
electric field – induced polarization and electrostatic
forces on the uncharged bodies
Reading Assignment : Chapter 21.5- 21.7
Next Lecture – in-class quiz about the material
we covered (chapter 21 )
Homework Assignment:
Check www.masteringphysics.com this afternoon
Due next Tuesday by end of class