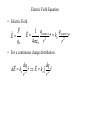Download Document

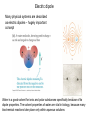
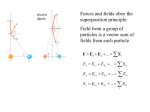
Example: Find the electric field at point P
Rework of this example (21.6 in book)
r
q
E  k 2 rˆ
r
r
r (1.2m)iˆ  (1.6m) ˆj
rˆ  
 0.6iˆ  0.8 ˆj
r
2.0m
9
r
9
2
2 8.0  10 C
E  (9.0  10 Nm /C )
(0.6iˆ  0.8 ˆj )
2
(2.0m)
r
E  (11N /C)iˆ  (14N /C) ˆj

Forces and fields obey the superposition principle:
Field from a group of particles is a vector sum of fields
from each particle
E  E1  E 2  ...   Ei
i
E x  E1x  E2 x  ...   Eix
i
E y  E1 y  E2 y  ...   Eiy
i
E z  E1z  E2 z  ...   Eiz
i
Electric Field Properties
• A small positive test charge is used to determine the
electric field at a given point
• The electric field is a vector field that can be symbolized
by lines in space called electric field lines
• The electric field is continuous, existing at every point, it
just changes in magnitude with distance from the source
Electric Field Equation
• Electric Field

 F
E
qo

1 qsource
qsource
E
rˆ  ke 2 rˆ
2
4 o r
r
• For a continuous charge distribution


dq
dq
dE  ke 2 rˆ  E  ke  2 rˆ
r
r
For spatially distributed charges – we can sub-divide the object into the small,
“point-like” charges and integrate (sum up) the individual fields.
Often, we assign charge density for such spacious charged objects
 ...   ... dq
i
dq   dl  for lines (1  d )
dq   dA  for surfaces (2  d )
dq   dV  for volumes (3  d )
 ,  ,   correspond ing charge densities
 (r )
E.g. in 3 - d : E(r)  ke 
(r  r ) dV
3
| r - r |
x  x
E x ( x, y, z)  ke 
(x,y,z) dx dy dz
2
2
2 3/ 2
(( x  x)  ( y  y )  ( z  z ) )
Examples of field calculations: fields of continuous charge
distributions
Field of a ring of charge on the symmetry axis
Ex   dEx
E x   ke

dQ
dQ
cos


k
 e x2  a2
r2
E  Ex 
kQx
( x 2  a 2 )3/ 2
x
x2  a2
Positive charge is uniformly distributed
around a semicircle. The electric field
that this charge produces at the center of
curvature P is in
A. the +x-direction.
B. the –x-direction.
C. the +y-direction.
D. the –y-direction.
E. none of the above
Field of a disk, uniformly charged on the symmetry axis
Surface charge density is , radius R
Area dA of a ring of radius r
dA  2 rdr; 
R
rdr
E x  2 ke x  2 2 3/ 2
(x  r )
0
E x  kex
x 2 R 2

x2
x2  r2  z
dz  2rdr
1 x 2 R 2
dz
x 2
3 / 2  2k ex
z
 z 
dQ
; dQ  2 r dr
dA
Changing variable of integration

 
x
Ex 
1 

2
2
2 0 
R  x 
For the limit of x<<R, we have an electric field of the infinite
plane sheet of charge and it is independent of the distance from
the plane (assuming that distance x<<linear dimensions of the sheet)

E plane 
2 0
Electric Field Line Properties
• Relation between field lines and electric field vectors:
a. The direction of the tangent to a field line is the direction of
the electric field E at that point
b. The number of field lines per unit area is proportional to the
magnitude of E: the more field lines the stronger E
• Electric field lines point in direction of force on a positive test
charge therefore away from a positive charge and toward a
negative charge
• Electric field lines begin on positive charges and end on negative
charges or infinity
• No two electric field lines can cross
Electric field lines
E is tangent to the electric field line – no 2 lines can
cross (E is unique at each point)
Magnitude of E is proportional to the density of the
lines
Remember, electric field lines are NOT trajectories!
When a particle moves on a curved path, the direction of
acceleration (and hence of the force) is not collinear with the
tangent to the curve
Electric dipole
Many physical systems are described
as electric dipoles – hugely important
concept
Water is a good solvent for ionic and polar substances specifically because of its
dipole properties. The solvent properties of water are vital in biology, because many
biochemical reactions take place only within aqueous solutions
Torque on the electric dipole
r
r
p  qd
(electric dipole moment from “-” to “+”)
Electric field is uniform in space
Net Force is zero
 Torque is not zero
Net
  (qE )(d sin  )



  p E
(torque is a vector)
Stable and unstable equilibrium




p  E
p  E
Charge #2
Three point charges lie at the vertices of an
equilateral triangle as shown. Charges #2
and #3 make up an electric dipole.
The net electric torque that Charge #1 exerts
on the dipole is
+q
Charge #1
+q
y
–q
x
A. clockwise.
B. counterclockwise.
C. zero.
D. not enough information given to decide
Charge #3
Electric field of a dipole
E-field on the line connecting two charges
 1 1 
E  keq 2  2 
r2 r1 

-
A
+
E
r2
d
2 p ke
E 3
r

r1


E-field on the line perpendicular to the dipole’s axis
E  2E 2 sin

E2

E


2
 E2
d
r
E 2  ke
A
E1
-
q
r2
qd
E  ke 3
r
r
r
p
E  k e 3
r

when r>>d
+
d
General case – combination of the above two

 

3( p r )  p
E
r 3
5
r
r
Dipole’s Potential Energy
E-field does work on the dipole – changes its potential energy
Work done by the field (remember your mechanics class?)
dW   d   pE sin d
 
U p E
Dipole aligns itself to minimize its potential energy
in the external E-field.
Net force is not necessarily zero in the non-uniform
electric field – induced polarization and electrostatic
forces on the uncharged bodies
Reading assignment: 22.1 – 22.5