Download Document

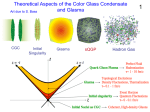
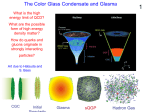
The High Energy Limit of QCD
The high energy limit is E -> infinity at fixed momentum transfer
Not short distance limit which is E -> infinity at fixed angle
Related Questions:
How do gluons and quarks arise in hadrons?
What are the possible forms of high density matter?
Claim: The high energy limit is controlled by a universal, high energy
density form of gluonic matter:
The Color Glass Condensate
In collisions, this matter produces a Glasma with interesting topolgical and
dynamical properties
Lecture I: The Color Glass Condensate
Lecture II: The Glasma
1
How do we think about a high energy hadron?
Work in fast moving frame:
High Energy Limit is Small x Limit
2
The Gluon Wall:
Wavefunction has:
3 quarks
3 quarks plus 1 gluon
3 quarks plus 2 gluon
…….
3 quarks plus many gluons
Important matrix elements at high
energies have lots of gluons in them
3
In RHIC Collisions
Au-Au at 100GeV/Nucleon in each beam
About 1000 slow moving (small x) particles are
made in central collisions
4
Where do all the gluons go?
Cross sections for hadrons
rise very slowly with energy
But the gluon density rises
much more rapidly!
The high energy limit is the high
gluon density limit.
Surely the density must saturate
for fixed sizes of gluons at high
energy.
5
What is the Color Glass Condensate?
Glue at large x generates glue at small x
Glue at small x is classical field
Time dilation -> Classical field is glassy
High phase space density -> Condensate
Phase space density:
Attractive potential
Repulsive interactions
Density as high as it can be
Because the density is high
is small
is big
6
There must be a renormalization group
The x which separates high x sources from small x fields is arbitrary
Phobos multiplicity data
High energy QCD “phase” diagram
7
Why is the Color Glass Condensate Important?
It is a new universal form of matter:
Matter: Carries energy; Separation of gluons is small
compared to size of system; Number of gluons is large
New: Can only be made and probed in high energy collsions
Universal: Independent of hadron, renormalization group
equations have a universal solution.
Universality <=> Fundamental
It is a theory of:
Origin of glue and sea quarks in hadrons
Cross sections
Initial conditions for formation of Quark Gluon Plasma in
heavy ion collisions
8
What does a sheet of Colored Glass look like?
On the sheet
is small
Independent of
big
small
Lienard-Wiechart potentials
Random Color
Density of gluons per unit area
9
The Color Glass Condensate Explains Growth of
Gluons at Small x
Renormalization group equation predicts:
Gluon pile up at fixed size until
gluons with strength
act like a hard sphere
Once one size scale is filled
Move to smaller size scale
Typical momentum scale grows
10
The CGC Explains Slow Growth of Total
Cross Section
Transverse distribution of gluons:
Transverse profile set by initial conditions
Size is determined when probe sees a fixed number of
particles at some transverse distance
11
CGC Explains Qualitative Features of
Electron-Hadron Scattering
Q is resolution momentum of
photon, x is that of struck quark
Function only of a particular
combination of Q and x
Scaling relation
Works for
Can successfully describe
quark and gluon
distributions at small x
and wide range of Q
12
CGC Gives Initial Conditions for QGP in
Heavy Ion Collisions
Two sheets of colored glass collide
Glass melts into gluons and
thermalize
QGP is made which expands into a
mixed phase of QGPand hadrons
Mystery: The QGP is very
strongly interacting:
Arnold and Moore suggest
heating may be due to
instabilities in melting CGC
13
CGC predicted particle production at RHIC
Proportionality constant can be
computed.
14
CGC provides a theory of shadowing (modification of
quark and gluon distributions in nuclei)
Two effects:
Multiple scattering: more particles at high pT
CGC modification of evolution equations => less particles
15
Data from dA collisions at RHIC Consistent with CGC
Look for fragments of deuteron since
they measure them smallest x
properties of the nucleus
Back to back jet correlations seen in
STAR?
Detailed studies of x dependence?
16
Future studies of CGC at RHIC, LHC, and eRHIC
At RHIC:
Systematic pA studies; Many exciting possibilities
Study and discover the QGP; Discover the CGC
LHC:
Can study at very small x with very high resolution
Study the CGC
eRHIC:
Precision experiments and tests
Careful and systematic study of CGC
17
Glasma
Definition:
The matter which is produced by the Color Glass Condensate
immediately after the collision
It is not a glass, evolving on a natural time scale
It has components which are highly coherent,
Components which are particle like
Components of strength in between
Initially it has large longitudinal color electric and color
magnetic fields, and maximal topological charge density
18
Choose A = 0 in backward light cone.
In left and right halves, pure gauge.
Discontinuity across light cone to match
color charge sources on light cone
Field is not pure gauge in forward
lightcone
Physical motivation: Renormalization group description.
In center of mass frame, degrees of freedom with
are coherent fields.
Larger y are sources
19
Before the collision, two sheets of mutually transverse color electric and color
magnetic fields.
Boosted Coulomb fields
Random in color
Thickness of sheets is
20
Initial fields:
In radial gauge,
the fields in the forward light cone are:
Assume boost invariant solution
21
Boundary conditions are determined by solving equations across the light
cone:
Infinitesmally after the collision there are
No transverse fields
Longitudinal magnetic and electric fields
22
These fields have a local topological charge density
Chern-Simons charge
The Chern-Simons charge density is maximal!
and has a transverse correlation length
23
How do the sources of color magnetic
and color electric field arise?
In forward light cone,
the vector potential
from one nucleus can
multiply the CGC field
from the other.
Equal and opposite
densities of charge
24
However:
Glasma fields are initial conditions, not a solution to
time independent equation of motion:
Unlike the constant field where
there is no magnetic field
25
The Glasma has three components:
Coherent classical fields:
Hard particles:
Degrees of freedom which can be described as either hard
particles or coherent fields
The Glasma has mostly evaporated by a time
During this time, scattering among the hard modes (parton cascade) is
not important
26
Interactions in the coherent fields takes place on a scale of order 1/Qs
Because of coherence, interactions of hard particles with the classical fields,
g x 1/g ~ 1
Also take place on a time scale 1/Qs
Very rapid strongly interacting system
But boost invariance is a problem, as this does not allow
longitudinal momentum to become thermalized
Important for two reasons:
Almost certainly instabilities of the hard-soft coupled system
under boost non-invariant perturbations
Can these instabilities generate either rapid thermalization or
isotropization of momentum?
27
Consequence of nonzero Chern-Simons
Charge: Vorticity Generation
Positively charged particle accelerates along E,
rotates in clockwise direction
Negatively charged particle accelerates along -E,
Rotates in anticlockwise direction
Net vorticity generation
Physical origin of t Hooft anomaly
28
Exciting times for theory:
Beginning of a complete description of high
energy limit of QCD
Must understand the collective excitations of
the CGC: pomerons, reggeons, odderons…
Need to understand interactions of these
collective excitations: ploops or Pomeron
loops
29