Download Statistical Models for Steganography - uni

Statistical models for
Secure Steganography
Systems
N.Muthiyalu Jothir
Media Informatics
5/25/2017
DRM Seminar
1
Agenda
Introduction
 Steganography
 Information theory
 Security Model
 Limitations
 Conclusion

5/25/2017
DRM Seminar
2
Introduction

“Steganography is the art and science of
writing hidden messages in such a way
that no one apart from the intended
recipient knows of the existence of the
message”

“Covered or Hidden Writing”
5/25/2017
DRM Seminar
3
Steganography Vs Cryptography

Steganography is the dark cousin of
cryptography, the use of codes.

Cryptography  Privacy

Steganography  Secrecy
5/25/2017
DRM Seminar
4
Digital Still Images

Larger the cover message – Easier to hide
message

For example: a 24-bit bitmap image will have 8
bits representing each of the three color values
(R,G,B)

Watermarking, Fingerprinting etc.
5/25/2017
DRM Seminar
5
Information Theory

“The fundamental problem of
communication is that of reproducing at
one point either exactly or approximately a
message selected at another point.”
-C.E. Shannon, 1948
5/25/2017
DRM Seminar
6
Information Theory …cont

According to Shannon, the entropy of a random variable X with
probability distribution PX and alphabet ‫ א‬is defined as

indicates the amount of information contained in x, i.e., the number of
bits needed to code x.

For example, in an image with uniform distribution of gray-level
intensity, i.e. Px = 1/256, then the number of bits needed to code each
gray level is 8 bits. The entropy of this image is 8.
5/25/2017
DRM Seminar
7
…cont

Information  "only infrmatn esentil fo
understandn mst b tranmitd."

The amount of information, or uncertainty, output
by an information source is a measure of its
entropy.

In turn, a source's entropy determines the
amount of bits per symbol required to encode
the source's information.
5/25/2017
DRM Seminar
8
Relative Entropy

Let p and q be two probability distributions on a
common alphabet X. Relative entropy / Kullback
Leibler “distance” between p and q is defined as

D(p || q) is a measure of the inefficiency of assuming
that the distribution is q when the true distribution is p.
5/25/2017
DRM Seminar
9
Security Model : Proposed

An information-theoretic model

Presence of passive adversaries

“Simmons' Prisoners‘ Problem"

“Hypothesis” testing problem
5/25/2017
DRM Seminar
10
Active adversaries

Presence of hidden message is known
Publicly

E.g., Watermarking and Fingerprinting.
5/25/2017
DRM Seminar
11
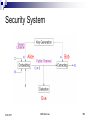
Scenario with Passive Adversaries

Players  Alice and Bob

Passive Adversary  Eve

“Cover Text, C”  Original, unaltered message

“Stegotext, S”  Transformed message using
Secret Key.
5/25/2017
DRM Seminar
12
Hypothesis testing
Eve, the decision maker
5/25/2017
DRM Seminar
13
Model

The security of a steganographic system is
quantified in terms of the relative entropy
D(PC | PS) (or discrimination) between PC
and PS.

D(PC | PS) = 0  stego system is perfectly
secure
5/25/2017
DRM Seminar
14
Security System
5/25/2017
DRM Seminar
15
Observations

H(S / CEKR) = 0  Certainty

H(E) > 0  Uncertainty

H(E / SK) = 0  Certainty
5/25/2017
DRM Seminar
16
…cont

Alice is inactive  she sends cover text C

Active  S is a concatenation of multiple
messages from Alice

The probability distributions of cover text
(Pc) are assumed to be known to all
parties
5/25/2017
DRM Seminar
17
Security Definition

Definition 1 :
A stegosystem as defined previously with cover
text C and stegotext S is called Є – secure
against passive adversaries if
D(PC|PS) ≤ Є

If Є = 0, the stegosystem is called perfectly
secure.
5/25/2017
DRM Seminar
18
Eve's decision process
Binary partition (C0, C1) of the set C of
possible cover texts
 Alice is active if and only if the observed
message ‘c’ is contained in C1.
 Type II error  Eve fails to detect

 Probability

β
Type I error  Eve accuses Alice when
she is inactive.
 Probabilty
5/25/2017
ά. Assumed to be zero.
DRM Seminar
19
Theorem

The stegosystem that is Є-secure against
passive adversaries, satisfy
d(ά, β) ≤ Є

In particular, if ά = 0, then
β = 2-Є
5/25/2017
DRM Seminar
20
…cont

In a perfectly secure system,
D(PC|PS) = 0  PC = PS;
Thus, Eve can obtain no information about
whether Alice is active by observing the
message.
5/25/2017
DRM Seminar
21
External Information Influence

The modified stegosystem with external
information Y , cover text C, and stegotext
S is called Є - secure against passive
adversaries if
D(PC|Y |PS|Y ) ≤ Є
5/25/2017
DRM Seminar
22
One-time pad

Security  The stegotext distribution is close to the
cover text distribution without knowledge of the key.

Cover text C is a uniformly distributed n-bit string

The key generator chooses the n-bit key K

S=e
5/25/2017
K and Bob can decode by computing e = S
DRM Seminar
K
23
Security of One Time Pad




Uniformly distributed in the set of n-bit strings and
therefore D(PC|PS) = 0.
Perfect steganographic security
One-time pad system is equivalent to the basic scheme
of visual cryptography
But,
Wardens never allow random messages  Drawback
5/25/2017
DRM Seminar
24
Universal Data Compression

Traditional data compression techniques
Huffman coding
 require a priori knowledge about the distribution of the
data


Universal data compression algorithms
Lempel and Ziv
 source statistics are unknown a priori or vary with time

5/25/2017
DRM Seminar
25
Willems' Repetition algorithm
Parameters  block length L and delay D
 Binary source X producing {Xt} = X1, X2,…
with values in {0,1}.
 Source output is divided into blocks Y1,
Y2… of length L
 Encoding of a block Yt operates by
considering


5/25/2017
Repetition time, the length of the interval since its last
occurrence.
DRM Seminar
26
…cont

Repetition time is encoded using the following
code

where || denotes the concatenation of the bit
strings.
5/25/2017
DRM Seminar
27
The Modification for Information
Hiding

Information hiding takes place if the encoder
or the decoder encounters a block y such that
ty ≥ 1/ρ

If this is the case, bit j of the message m is
embedded in y’ according to
5/25/2017
DRM Seminar
28
Limitations

Embedding distortion DEmb can be large for
the same secure statistics

Future work by Joachim and Bernd,
address the above issue.
5/25/2017
DRM Seminar
29
Conclusion
A security model has been proposed
 Forms the basis for the hypothetical
testing scenario
 Security of the Steganography system
depends on the relative entropy between
C and S.

5/25/2017
DRM Seminar
30
References
1.
Christian Cachin, “An Information - Theoretic Model for
Steganography”, Cambridge, 1998.
2.
Joachim, Bernd, “A Communications Approach to
Image Steganography”, Proceedings of SPIE, Jan
2002.
5/25/2017
DRM Seminar
31
Thank You…
5/25/2017
DRM Seminar
32