Fractions Practice Puzzles
... get students excited about math. This book combines basic fraction problems with loads of hilarious riddles guaranteed to get students revved up for learning. As you may know, one of the keys to helping students learn successfully is to make learning fun. That’s why each page of Fractions Practice P ...
... get students excited about math. This book combines basic fraction problems with loads of hilarious riddles guaranteed to get students revved up for learning. As you may know, one of the keys to helping students learn successfully is to make learning fun. That’s why each page of Fractions Practice P ...
Fraction Puzzles
... get students excited about math. This book combines basic fraction problems with loads of hilarious riddles guaranteed to get students revved up for learning. As you may know, one of the keys to helping students learn successfully is to make learning fun. That’s why each page of Fractions Practice P ...
... get students excited about math. This book combines basic fraction problems with loads of hilarious riddles guaranteed to get students revved up for learning. As you may know, one of the keys to helping students learn successfully is to make learning fun. That’s why each page of Fractions Practice P ...
Solutions
... Solution 1 by Lisa Fukui (12): At least three edges must meet at every vertex of a polyhedron. If a polyhedron had n vertices and every vertex had different numbers of edges meeting, then the number of edges meeting at the vertex with the most edges would be at least n + 2 . A polyhedron with n vert ...
... Solution 1 by Lisa Fukui (12): At least three edges must meet at every vertex of a polyhedron. If a polyhedron had n vertices and every vertex had different numbers of edges meeting, then the number of edges meeting at the vertex with the most edges would be at least n + 2 . A polyhedron with n vert ...
Recursion
... "One Small Step/Complete the Solution" • Each invocation of a recursive function performs one small step towards the entire solution and makes a recursive call to complete the solution. ...
... "One Small Step/Complete the Solution" • Each invocation of a recursive function performs one small step towards the entire solution and makes a recursive call to complete the solution. ...
Efficient Pseudorandom Generators Based on the DDH Assumption
... curve over a prime field Fp such that p is close to 2256 . Let q denote the order of the curve. On input s0 chosen uniformly at random from Zq the Dual Elliptic Curve generator produces two sequences of points si P and si Q such that si is set to be the x-coordinate of si−1 P , i = 1, 2, . . . , k. ...
... curve over a prime field Fp such that p is close to 2256 . Let q denote the order of the curve. On input s0 chosen uniformly at random from Zq the Dual Elliptic Curve generator produces two sequences of points si P and si Q such that si is set to be the x-coordinate of si−1 P , i = 1, 2, . . . , k. ...
LifeCare PCA Infusion System With Hospira MedNet Software
... two minutes. ♦ The History Key is used to review current program, dose history, and event log. It also provides access to the Print History soft key. The Print History soft key is only functional if a printer is attached to the device. ♦ The Start/ Pause key is used to start and pause an infusion. ♦ ...
... two minutes. ♦ The History Key is used to review current program, dose history, and event log. It also provides access to the Print History soft key. The Print History soft key is only functional if a printer is attached to the device. ♦ The Start/ Pause key is used to start and pause an infusion. ♦ ...
Introduction To Modular Arithmetic
... Recall that if you move to the left of 0 on a number line, you get negative numbers. Similarly, going in the opposite direction (counterclockwise) on the number circle, we get to negative numbers in modular arithmetic. For example, 1 ⌘ 11 (mod 12), ...
... Recall that if you move to the left of 0 on a number line, you get negative numbers. Similarly, going in the opposite direction (counterclockwise) on the number circle, we get to negative numbers in modular arithmetic. For example, 1 ⌘ 11 (mod 12), ...
An Efficient Scheme for Proving a Shuffle
... shuffle. We take a completely different approach than that of [SK95] and [Ab99]. We represent a permutation by a matrix, and introduce two conditions which suffice to achieve a permutation matrix. We then present zero-knowledge proofs to prove the satisfiability of each condition. Moreover, these tw ...
... shuffle. We take a completely different approach than that of [SK95] and [Ab99]. We represent a permutation by a matrix, and introduce two conditions which suffice to achieve a permutation matrix. We then present zero-knowledge proofs to prove the satisfiability of each condition. Moreover, these tw ...
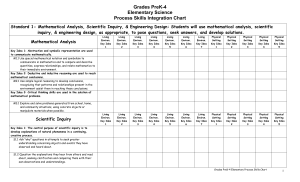
154 kb - Mahopac Central School District
... descriptions of objects and events and to from their own tentative explanations of what they have observed. Key Idea 2: Beyond the use of reasoning & consensus, scientific inquiry involves the testing of proposed explanations involving the use of conventional techniques & procedures & usually requir ...
... descriptions of objects and events and to from their own tentative explanations of what they have observed. Key Idea 2: Beyond the use of reasoning & consensus, scientific inquiry involves the testing of proposed explanations involving the use of conventional techniques & procedures & usually requir ...
Full text
... No odd multiperfect numbers are known. In many papers concerned with odd perfect numbers (summarized in McDaniel & Hagis [5]), values have been obtained which cannot be taken by the even exponents on the prime factors of such numbers, if all those exponents are equal. McDaniel [4] has given results ...
... No odd multiperfect numbers are known. In many papers concerned with odd perfect numbers (summarized in McDaniel & Hagis [5]), values have been obtained which cannot be taken by the even exponents on the prime factors of such numbers, if all those exponents are equal. McDaniel [4] has given results ...
Attestation
... Creates 2048-bit RSA Storage Root Key (SRK) on TPM Cannot run TPM_TakeOwnership again: Ownership Enabled flag False Done once by IT department or laptop owner. (optional) Step 2: TPM_CreateWrapKey Create more RSA keys on TPM certified by SRK Each key identified by 32-bit keyhandle ...
... Creates 2048-bit RSA Storage Root Key (SRK) on TPM Cannot run TPM_TakeOwnership again: Ownership Enabled flag False Done once by IT department or laptop owner. (optional) Step 2: TPM_CreateWrapKey Create more RSA keys on TPM certified by SRK Each key identified by 32-bit keyhandle ...
Datasäkerhet/Data security EDA625 – Lect2 CRYPTOGRAPHY
... strong collision resistance: it is infeasable to find x,x’ such that h(x)=h(x’) ...
... strong collision resistance: it is infeasable to find x,x’ such that h(x)=h(x’) ...
MOD p LOGARITHMS log2 3 AND log3 2 DIFFER FOR
... We may consider a generalization of problem 2 into the setting of group schemes. Let A/Q be an abelian group scheme over Q (we understand under this notion a group scheme [B] whose group structure is abelian without further restrictions, cf. [Mi] for narrower definition), with some reasonably good m ...
... We may consider a generalization of problem 2 into the setting of group schemes. Let A/Q be an abelian group scheme over Q (we understand under this notion a group scheme [B] whose group structure is abelian without further restrictions, cf. [Mi] for narrower definition), with some reasonably good m ...
21. immobilizer system (hiss)
... 1. Obtain a new ignition switch and two new transponder keys. 2. Remove the ignition switch (page 20-20). 3. Apply 12 V battery voltage to the CKP sensor lines of the ECM using the special tool (page 21-7). 4. Set the original (registered) key near the immobilizer receiver so that the transponder in ...
... 1. Obtain a new ignition switch and two new transponder keys. 2. Remove the ignition switch (page 20-20). 3. Apply 12 V battery voltage to the CKP sensor lines of the ECM using the special tool (page 21-7). 4. Set the original (registered) key near the immobilizer receiver so that the transponder in ...
TAKA_10v1_public-key cryptosystems bsed on CR
... The random choice of r, Pr[AskH]=O(qH/2t) in any case, qH=#(queries asked to the oracle H) and 0≦r<2t. G and H are seen like random oracles, the attacker has no chance to correctly guess b, during a real attack. ...
... The random choice of r, Pr[AskH]=O(qH/2t) in any case, qH=#(queries asked to the oracle H) and 0≦r<2t. G and H are seen like random oracles, the attacker has no chance to correctly guess b, during a real attack. ...
Slides
... There is a meet-in-the-middle key recovery attack for AES-128. It requires 2126 operations, so it is only about four times faster than brute-force. There is a “related key” attack on AES-192 and AES-256. This means that if you use two keys that are related in a certain way, the security may be reduc ...
... There is a meet-in-the-middle key recovery attack for AES-128. It requires 2126 operations, so it is only about four times faster than brute-force. There is a “related key” attack on AES-192 and AES-256. This means that if you use two keys that are related in a certain way, the security may be reduc ...
Application research and analysis based on Bitlocker
... The computer system With TPM1.2 trusted platform module product system startup key (StartupKey) and system restore key (Recovery Password)in the use of Bitlocker encryption system boot disk. The startup key is of encrypted form, system restore key is of non-encrypted form. Each key has a correspondi ...
... The computer system With TPM1.2 trusted platform module product system startup key (StartupKey) and system restore key (Recovery Password)in the use of Bitlocker encryption system boot disk. The startup key is of encrypted form, system restore key is of non-encrypted form. Each key has a correspondi ...
Lecture 9 - MyCourses
... The Private Exponent ◮ If we can compute the private exponent then we can factor n with at least probability 1/2. Repeating m times gives success probability 1 − (1/2)m . ◮ Las Vegas algorithm is a randomized algorithm which may fail to give an answer, but if it gives an answer, the answer is corre ...
... The Private Exponent ◮ If we can compute the private exponent then we can factor n with at least probability 1/2. Repeating m times gives success probability 1 − (1/2)m . ◮ Las Vegas algorithm is a randomized algorithm which may fail to give an answer, but if it gives an answer, the answer is corre ...
Solutions to Midterm 1
... We need to nd two elements x ∈ U (999) = {a ∈ N | a < 999 & gcd (a, 999) = 1} such that x2 = 1, the identity element of U (999). Let us forget about modular arithmetic for a moment and solve x2 = 1 with algebra: x = 1 and x = −1. x = 1 ∈ U (999) (gcd(1, 999) = 1), but −1 ∈ / U (999) since −1 is not ...
... We need to nd two elements x ∈ U (999) = {a ∈ N | a < 999 & gcd (a, 999) = 1} such that x2 = 1, the identity element of U (999). Let us forget about modular arithmetic for a moment and solve x2 = 1 with algebra: x = 1 and x = −1. x = 1 ∈ U (999) (gcd(1, 999) = 1), but −1 ∈ / U (999) since −1 is not ...
A Survey of BGP Security: Issues and Solutions
... Provides Encryption/Authentication of IP Packets Also Provides Needed Key Infrastructure Ubiquitous, Well-Understood, Easy to Use Two Protocols with Differing Security: AH/ESP Only Provides Pairwise Protection ...
... Provides Encryption/Authentication of IP Packets Also Provides Needed Key Infrastructure Ubiquitous, Well-Understood, Easy to Use Two Protocols with Differing Security: AH/ESP Only Provides Pairwise Protection ...
Cryptographic hashing - comp
... how to interpret these data fields, in terms of their lengths, for example. ...
... how to interpret these data fields, in terms of their lengths, for example. ...
Verifiable Shuffling
... V accepts the proof if and only if all of the equations in (12) hold. (Note that the left hand side of each of the equations in 12 can be evaluated using the technique of simultaneous multiple exponentiation resulting in an effective reduction of the complexity of evaluating all of them from 4k expo ...
... V accepts the proof if and only if all of the equations in (12) hold. (Note that the left hand side of each of the equations in 12 can be evaluated using the technique of simultaneous multiple exponentiation resulting in an effective reduction of the complexity of evaluating all of them from 4k expo ...
Diffie–Hellman key exchange
Diffie–Hellman key exchange (D–H) is a specific method of securely exchanging cryptographic keys over a public channel and was one of the first public-key protocols as originally conceptualized by Ralph Merkle. D–H is one of the earliest practical examples of public key exchange implemented within the field of cryptography. The Diffie–Hellman key exchange method allows two parties that have no prior knowledge of each other to jointly establish a shared secret key over an insecure channel. This key can then be used to encrypt subsequent communications using a symmetric key cipher.The scheme was first published by Whitfield Diffie and Martin Hellman in 1976. By 1975, James H. Ellis, Clifford Cocks and Malcolm J. Williamson within GCHQ, the British signals intelligence agency, had also shown how public-key cryptography could be achieved; however, their work was kept secret until 1997.Although Diffie–Hellman key agreement itself is a non-authenticated key-agreement protocol, it provides the basis for a variety of authenticated protocols, and is used to provide perfect forward secrecy in Transport Layer Security's ephemeral modes (referred to as EDH or DHE depending on the cipher suite).The method was followed shortly afterwards by RSA, an implementation of public-key cryptography using asymmetric algorithms.U.S. Patent 4,200,770, from 1977, is now expired and describes the now public domain algorithm. It credits Hellman, Diffie, and Merkle as inventors.