* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download TAKA_10v1_public-key cryptosystems bsed on CR
Survey
Document related concepts
Transcript
Public-Key Cryptosystems Based on
Composite Degree Residuosity Classes
EUROCRYPT'99, LNCS 1592, pp. 223-238, 1999.
By Pascal Paillier
Efficient Public-Key Cryptosystem
Provably Secure against Active Adversaries
ASIACRYPT'99, LNCS 1716, pp. 165-179, 1999.
By Pascal Paillier and David Pointcheval
Presenter: 陳國璋
Outline
Introduction
Notation and math. assumption
Scheme 1
Scheme 2
Scheme 3
Properties
Conclusion
Introduction(1/2)
兩個主要的Trapdoor技術
RSA
Diffie-Hellman
提出新的技術
Composite Residuosity
提出新的計算性問題
Composite Residuosity Class Problem
Introduction(2/2)
提出3個架構在上述假設的同態加密機制
(Homomophic encryption schemes),
之中包含一個新的trapdoor permutation
作者提出證明, scheme具有抵抗adaptive
chosen-ciphertext attack(IND-CCA2)
in the random oracle.
Outline
Introduction
Notation and math. assumption
Scheme 1
Scheme 2
Scheme 3
Properties
Conclusion
Notation(1/3)
p, q are two large primes.
n = pq
Euler phi-function
ψ(n) = (p-1)(q-1)
Notation(2/3)
Carmichael function
λ(n) = lcm(p-1,q-1)
|Zn2*| = ψ(n2) = nψ(n)
By Carmichael theorem, Any w∈Zn2*,
wλ = 1 mod n
wnλ = 1 mod n2
Notation(3/3)
RSA[n,e] problem
c = me mod n
Extracting eth roots modulo n.
Relation P1 P2 (resp. P1≡P2) will
denoted that problem P1 is polynomial
reducible to the problem P2.
Deciding Composite Residuosity
(1/5)
nth residue modulo n2
A number z is the nth residue modulo
n2 if there exist a number y such that
z = yn mod n2
Deciding Composite Residuosity
(2/5)
CR[n] problem
deciding nth residuosity.
Distinguishing nth residues from non nth
residues.
The CR[n] problem of deciding
quadratic or higher degree residuosity,
it is a random-self-reducibility
problem.
Deciding Composite Residuosity
(3/5)
self-reducible
A function f evaluating any instance x
can be reduced in polynomial time to the
evaluation of f on one or more random
instances yi.
Deciding Composite Residuosity
(4/5)
Random-self-reducible
In the domain of f, an arbitrary worst-case
instance x is mapped to a random set of
instances y1,…,yk.
f(x) can be computed in polynomial time, and
then f(y1),…,f(yk) are taking the average with
respect to the induced distribution on yi.
The average case complexity of f is the same as
the worse case randomized complexity of f.
All of its instances are polynomially equivalent.
Deciding Composite Residuosity
(5/5)
There exists no polynomial time
distinguisher for nth residues modulo
n2, i.e. CR[n] is intractable.
Computing Composite Residuosity
Class(1/13)
g∈Zn2*
εg: Zn × Zn* → Zn2* be a integervalued function defined by
εg(x,y) = gx yn mod n2
Computing Composite Residuosity
Class(2/13)
Bα⊂ Zn2*
The set of elements of order nα
Set B is their disjoint union for
α=1,…,λ
Computing Composite Residuosity
Class(3/13)
If the order of g is a nonzero multiple
of n them εg is bijective.
εg: Zn × Zn* → Zn2* by εg(x,y) = gx yn mod n2
Two groups Zn × Zn* and Zn2* have the
same order nψ(n). i.e. εg is surjective.
Assume g x1 y1n g x2 y2n mod n 2
g
x2 x1
y2 n
( ) 1 mod n 2
y1
1. Since, g ( x2 x1 ) 1 mod n 2
( x2 x1 ) is a multiple of g's order.
it is a multiple of n.
gcd( , n) 1
( x2 x1 ) is a multiple of n.
x2 x1
2. (
y2 n
) 1 mod n 2
y1
y2
1 over Z n*
y1
y2 y1
By part 1 and 2, hence, g is injective.
Computing Composite Residuosity
Class(5/13)
g B, for w Z ,
*
n2
we call that n-th residuosity class of w with respect to g ,
the unique integer x Z n y Z s.t. g ( x, y ) w
*
n
the class of w is denoted [w]g
Computing Composite Residuosity
Class(6/13)
[w]g 0 w is a n-th residue modulo n
*
w
,
w
Z
1 2 n , [ w1w2 ]g [ w1 ]g [ w2 ]g mod n
2
the class function w [ w]g is a homomorphism
from ( Z n*2 , ) to ( Z n , ), g
2
Computing Composite Residuosity
Class(7/13)
Class[n,g] problem
nth Residuosity Class Problem of base g
Computing the class function in base g
given w∈Zn2*, compute [w]g
random-self-reducible problem
the bases g are independent
Computing Composite Residuosity
Class(8/13)
Class[n,g] problem is random-selfreducible problem over w∈Zn2*
Easily transform any w∈Zn2* into a
random instance w’∈Zn2* with uniform
distribution.
By w’=wgαβn mod n2 where αandβ are
taken uniform at random over Zn.
After [w’]g has been computed, it is so
simply to return [w]g=[w’]g-α mod n.
Computing Composite Residuosity
Class(9/13)
Class[n,g] is random-self-reducible over
g∈B, i.e.∀g1,g2∈B,Class[n,g1]≡Class[n,g2]
For Class[n,g] problems, the bases g are
independent. We can to look upon it as a
computational problem which purely relies
on n.
Class[n] problem
Computational composite residuosity class
problem
given w∈Zn2* and g∈B, compute [w]g
Computing Composite Residuosity
Class(10/13)
set S n {u n 2 | u 1 mod n}
is multiplicative subgroup of mod n
2
over which the function L such that
u 1
u Sn , L(u )
is clearly well-defined.
n
*
2
w
Z
,
L
(
w
mod
n
)
[
w
]
mod
n
2
1
n
n
Computing Composite Residuosity
Class(11/13)
Class[n] Fact[n]
Class[n] RSA[n, n]
D-Class[n] problem
decisional Class[n] problem
given w∈Zn2*,g∈B, x∈Zn, decide whether x=[w]g
or not
CR[n] D Class[n] Class[n]
Computing Composite Residuosity
Class(12/13)
Fact[n]
The factorization of n.
RSA[n]
c = me mod n
Extracting eth roots modulo n
CR[n]
deciding nth residuosity.
Computing Composite Residuosity
Class(13/13)
Class[n]
Computational composite residuosity class
problem
given w∈Zn2* and g∈B, compute [w]g
D-Class[n]
decisional Class[n] problem
given w∈Zn2*,g∈B, x∈Zn, decide whether x=[w]g
or not
CR[n] D Class[n] Class[n] RSA[n, n] Fact[n]
Notions of Security(1/3)
Indistinguishability of encryption(IND)
Non-malleability(NM)
Given the encryption of a plaintext x, the
attack cannot produce the encryption of
a meaningfully related plaintext x’.(For
example, x’=x+1)
Notions of Security(2/3)
Chosen-plaintext attack (CPA)
Non-adaptive chosen-ciphertext
attack (CCA1)
Adaptive chosen-ciphertext attack
(CCA2)
IND-CCA2 and NM-CCA2 are strictly
equivalent notions.
Notions of Security(3/3)
Random Oracle Model
Hash functions are considered to be
ideal. i.e. perfect random.
From a security viewpoint, this
impacts by giving the attacker an
additional access to the random
oracles of the scheme.
Outline
Background
Notation and math. assumption
Scheme 1
Scheme 2
Scheme 3
Properties
Conclusion
Scheme 1(1/4)
New probabilistic encryption scheme
n pq and random base g B
s.t. gcd( L( g mod n ), n) 1
2
(n, g ) as public parameters;
( p, q) ( ) as private pair.
Scheme 1 (2/4)
•
Enc:
plaintext m n; random number r n
ciphertext c g m r n mod n 2
i.e. c = g (m, r )
(trapdoor function with as the trapdoor secret,
one-wayness iff Class[n] hold)
• Dec:
ciphertext c n 2
L(c mod n 2 )
plaintext m
mod n
2
L( g mod n )
u Sn , L(u )
u 1
is clearly well-defined.
n
Scheme 1 (3/4)
One-way function
Given x, to compute f(x) = y is easy.
Given y, to find x s.t. f(x) = y is hard.
One-way trapdoor
f() is a one-way function.
Given a secret s, given y, to find x s.t. f(x) = y is
easy.
Trapdoor permutation
f() is a one-way trapdoor.
f() is bijective.
Scheme 1 (4/4)
• For example:
n 5*7 35; n 2 1225
(n) 4*6 24; (n) lcm(4,6) 12
Take g 13 s.t. gcd( L(1312 mod 1225),35) 1
Let m 23, r 19
Enc: c 1323 1935 mod 1225 53
L(5312 mod 1225)
Dec: m
mod 35
12
L(13 mod 1225)
24
=
mod 35
33
u 1
-1
u
S
,
L
(
u
)
is clearly well-defined.
n
=24 33 mod 35
n
=23
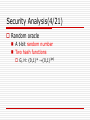
Security Analysis(1/21)
Against an adaptive chosenciphertext attack.(IND-CCA2)
In the scenario, the adversary makes
of queries of her choice to a
decryption oracle during two stages.
Security Analysis(2/21)
The first stage, the find stage
Attacker chooses two messages.
Requests encryption oracle to encrypted
one of them.
the encryption oracle makes the secret
choice of which one.
Security Analysis(3/21)
The second stage, the guess stage
To query the decryption oracle with
ciphertext of her choice.
Finally, she tell her guess about the
choice the encryption oracle made.
Security Analysis(4/21)
Random oracle
A t-bit random number
Two hash functions
G, H: {0,1}* →{0,1}|n|
Security Analysis(5/21)
Provided t=Ω(|n|δ) for δ>0, Scheme 1 is
semantically secure against adaptive
chosen-ciphertext attacks (IND-CCA2)
under the Decision Composite Residuosity
assumption (D-Class assumption) in the
random oracle.
D-Class[n]
decisional Class[n] problem
given w∈Zn2*,g∈B, x∈Zn, decide whether x=[w]g
or not
Security Analysis(6/21)
An adversary A=(A1,A2) against
semantic security of scheme 1.
A1: the find stage
A2: the guess stage
This adversary to efficiently decide nth
residuosity classes.
Security Analysis(7/21)
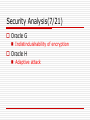
Oracle G
Indistinduishability of encryption
Oracle H
Adaptive attack
Security Analysis(8/21)
Simulation of the Decryption Oracle
The attacker asks for aciphertext c to be
decrypted.
The simulator checks in the queryhistory from the random oracle H.
Whether some entry leads to the
ciphertext c and then return m;
otherwise, it return “failure”.
Security Analysis(9/21)
Quasi-perfect simulation
The probability of producing a valid
ciphertext without asking the query (m,r)
to the random oracle H (whose answer a
has to satisfy the test an = z mod n) is
upper bounded by 1/ψ(n)≦2/n, which is
clearly negligible.
Security Analysis(10/21)
Initialization
n=pq, g∈Zn2*
Public: n,g
Private: λ
Security Analysis(11/21)
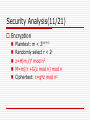
Encryption
Plaintext: m < 2|n|-t-1
Randomly select r < 2t
z=H(m,r)n mod n2
M=m||r +G(z mod n) mod n
Ciphertext: c=gMz mod n2
Security Analysis(12/21)
Decryption
Ciphertext: c=gMz mod n2 ∈Zn2*
M=[L(cλmod n2)/L(gλmod n2)] mod n
z’=g-Mc mod n
m’||r’=M-G(z’) mod n
If H(m’,r’)n = z’ mod n, then the plaintext
is m’
Otherwise, output “failure”
Security Analysis(13/21)
Attacker A to design a distinguisher B
for nth residuosity class.
(w,α) is a instance of the D-Class
problem, where α is the nth
residuosity class of w.
D-Class[n]
decisional Class[n] problem
given w∈Zn2*,g∈B, α∈Zn, decide whether
α=[w]g or not
Security Analysis(14/21)
Distinguisher B(1/2)
Randomly chooses u∈Zn, v∈Zn*, 0≦r<2t.
Compute the follows
z=wg-αvn mod n
c=wguvn mod n2
Run A1 and gets two messages m0,m1
Security Analysis(15/21)
Distinguisher B(2/2)
Chooses a bit b
Run A2 on the ciphertext c, supposed to
the ciphertext of mb and using the
random r.
Security Analysis(16/21)
Shut this game down
z is asked to the oracle G, shut this
game down and B return 1.
This event will be denote by AskG
If (m0,r) or (m1,r) are asked to the
oracle H, shut this geme down and B
return 0.
This event will be denote by AskH
In any other case, B return 0 when A2
end.
Security Analysis(17/21)
One event AskG or AskH is likely to
happen, B terminate the game.
The random choice of r,
Pr[AskH]=O(qH/2t) in any case,
qH=#(queries asked to the oracle H)
and 0≦r<2t.
G and H are seen like random oracles,
the attacker has no chance to
correctly guess b, during a real attack.
Security Analysis(18/21)
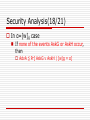
In α=[w]g case
If none of the events AskG or AskH occur,
then
AdvA ≦ Pr[ AskG ∨ AskH | [w]g = α]
Security Analysis(19/21)
In α≠[w]g case
z is perfectly random (independent of c),
then Pr[AskG] ≦ qG/ψ(n), qG=#(queries
asked to the oracle G) and u∈Zn, v∈Zn*,
z=wg-αvn mod n
Security Analysis(20/21)
• The advantage of distinguisher B in deciding
the nth residuosity classes:
AdvB
Pr[1|[ w]g ] Pr[1|[ w]g ]
Pr[ AskG |[ w]g ] Pr[ AskG |[ w]g ]
Pr[ AskG AskH |[ w]g ] Pr[ AskH |[ w]g ] Pr[ AskG |[ w]g ]
qH qG
AdvA t
2 ( n)
qH 2qG
AdvA t
2
n
Security Analysis(21/21)
• Reduction Cost
– If there exists an active attacker A against semantic
security, one can decide nth residuosity classes with
an advantage greater then
2 qD qH 2qG
AdvA (1 ) t
n
2
n
qG qD
qH
AdvA t 2
2
n























































![[Part 2]](http://s1.studyres.com/store/data/008795781_1-3298003100feabad99b109506bff89b8-150x150.png)





