Download TAKA_10v1_public-key cryptosystems bsed on CR

Public-Key Cryptosystems Based on
Composite Degree Residuosity Classes
EUROCRYPT'99, LNCS 1592, pp. 223-238, 1999.
By Pascal Paillier
Efficient Public-Key Cryptosystem
Provably Secure against Active Adversaries
ASIACRYPT'99, LNCS 1716, pp. 165-179, 1999.
By Pascal Paillier and David Pointcheval
Presenter: 陳國璋
Outline







Introduction
Notation and math. assumption
Scheme 1
Scheme 2
Scheme 3
Properties
Conclusion
Introduction(1/2)
 兩個主要的Trapdoor技術
 RSA
 Diffie-Hellman
 提出新的技術
 Composite Residuosity
 提出新的計算性問題
 Composite Residuosity Class Problem
Introduction(2/2)
 提出3個架構在上述假設的同態加密機制
(Homomophic encryption schemes),
之中包含一個新的trapdoor permutation
 作者提出證明, scheme具有抵抗adaptive
chosen-ciphertext attack(IND-CCA2)
in the random oracle.
Outline







Introduction
Notation and math. assumption
Scheme 1
Scheme 2
Scheme 3
Properties
Conclusion
Notation(1/3)
 p, q are two large primes.
 n = pq
 Euler phi-function
 ψ(n) = (p-1)(q-1)
Notation(2/3)
 Carmichael function
 λ(n) = lcm(p-1,q-1)
 |Zn2*| = ψ(n2) = nψ(n)
 By Carmichael theorem, Any w∈Zn2*,
 wλ = 1 mod n
 wnλ = 1 mod n2
Notation(3/3)
 RSA[n,e] problem
 c = me mod n
 Extracting eth roots modulo n.
 Relation P1  P2 (resp. P1≡P2) will
denoted that problem P1 is polynomial
reducible to the problem P2.
Deciding Composite Residuosity
(1/5)
 nth residue modulo n2
 A number z is the nth residue modulo
n2 if there exist a number y such that
z = yn mod n2
Deciding Composite Residuosity
(2/5)
 CR[n] problem
 deciding nth residuosity.
 Distinguishing nth residues from non nth
residues.
 The CR[n] problem of deciding
quadratic or higher degree residuosity,
it is a random-self-reducibility
problem.
Deciding Composite Residuosity
(3/5)
 self-reducible
 A function f evaluating any instance x
can be reduced in polynomial time to the
evaluation of f on one or more random
instances yi.
Deciding Composite Residuosity
(4/5)
 Random-self-reducible
 In the domain of f, an arbitrary worst-case
instance x is mapped to a random set of
instances y1,…,yk.
 f(x) can be computed in polynomial time, and
then f(y1),…,f(yk) are taking the average with
respect to the induced distribution on yi.
 The average case complexity of f is the same as
the worse case randomized complexity of f.
 All of its instances are polynomially equivalent.
Deciding Composite Residuosity
(5/5)
 There exists no polynomial time
distinguisher for nth residues modulo
n2, i.e. CR[n] is intractable.
Computing Composite Residuosity
Class(1/13)
 g∈Zn2*
 εg: Zn × Zn* → Zn2* be a integervalued function defined by
 εg(x,y) = gx yn mod n2
Computing Composite Residuosity
Class(2/13)
 Bα⊂ Zn2*
 The set of elements of order nα
 Set B is their disjoint union for
α=1,…,λ
Computing Composite Residuosity
Class(3/13)
 If the order of g is a nonzero multiple
of n them εg is bijective.
 εg: Zn × Zn* → Zn2* by εg(x,y) = gx yn mod n2
 Two groups Zn × Zn* and Zn2* have the
same order nψ(n). i.e. εg is surjective.
Assume g x1 y1n  g x2 y2n mod n 2
g
x2  x1
y2 n
( )  1 mod n 2
y1
1. Since, g  ( x2  x1 )  1 mod n 2
  ( x2  x1 ) is a multiple of g's order.
 it is a multiple of n.
gcd( , n)  1
 ( x2  x1 ) is a multiple of n.
 x2  x1
2. (
y2 n
)  1 mod n 2
y1
y2

 1 over Z n*
y1
 y2  y1
By part 1 and 2, hence,  g is injective.
Computing Composite Residuosity
Class(5/13)
g  B, for w  Z ,
*
n2
we call that n-th residuosity class of w with respect to g ,
the unique integer x  Z n  y  Z s.t.  g ( x, y )  w
*
n
the class of w is denoted [w]g
Computing Composite Residuosity
Class(6/13)
 [w]g  0  w is a n-th residue modulo n
*

w
,
w

Z
 1 2 n , [ w1w2 ]g  [ w1 ]g  [ w2 ]g mod n
2
the class function w  [ w]g is a homomorphism
from ( Z n*2 , ) to ( Z n , ), g
2
Computing Composite Residuosity
Class(7/13)
 Class[n,g] problem





nth Residuosity Class Problem of base g
Computing the class function in base g
given w∈Zn2*, compute [w]g
random-self-reducible problem
the bases g are independent
Computing Composite Residuosity
Class(8/13)
 Class[n,g] problem is random-selfreducible problem over w∈Zn2*
 Easily transform any w∈Zn2* into a
random instance w’∈Zn2* with uniform
distribution.
 By w’=wgαβn mod n2 where αandβ are
taken uniform at random over Zn.
 After [w’]g has been computed, it is so
simply to return [w]g=[w’]g-α mod n.
Computing Composite Residuosity
Class(9/13)
 Class[n,g] is random-self-reducible over
g∈B, i.e.∀g1,g2∈B,Class[n,g1]≡Class[n,g2]
 For Class[n,g] problems, the bases g are
independent. We can to look upon it as a
computational problem which purely relies
on n.
 Class[n] problem
 Computational composite residuosity class
problem
 given w∈Zn2* and g∈B, compute [w]g
Computing Composite Residuosity
Class(10/13)
 set S n  {u  n 2 | u  1 mod n}
is multiplicative subgroup of mod n
2
over which the function L such that
u 1
u  Sn , L(u ) 
is clearly well-defined.
n
*

2

w

Z
,
L
(
w
mod
n
)


[
w
]
mod
n

2
1

n
n
Computing Composite Residuosity
Class(11/13)
 Class[n]  Fact[n]
 Class[n]  RSA[n, n]
 D-Class[n] problem
 decisional Class[n] problem
 given w∈Zn2*,g∈B, x∈Zn, decide whether x=[w]g
or not
 CR[n]  D  Class[n]  Class[n]
Computing Composite Residuosity
Class(12/13)
 Fact[n]
 The factorization of n.
 RSA[n]
 c = me mod n
 Extracting eth roots modulo n
 CR[n]
 deciding nth residuosity.
Computing Composite Residuosity
Class(13/13)
 Class[n]
 Computational composite residuosity class
problem
 given w∈Zn2* and g∈B, compute [w]g
 D-Class[n]
 decisional Class[n] problem
 given w∈Zn2*,g∈B, x∈Zn, decide whether x=[w]g
or not
 CR[n]  D  Class[n]  Class[n]  RSA[n, n]  Fact[n]
Notions of Security(1/3)
 Indistinguishability of encryption(IND)
 Non-malleability(NM)
 Given the encryption of a plaintext x, the
attack cannot produce the encryption of
a meaningfully related plaintext x’.(For
example, x’=x+1)
Notions of Security(2/3)
 Chosen-plaintext attack (CPA)
 Non-adaptive chosen-ciphertext
attack (CCA1)
 Adaptive chosen-ciphertext attack
(CCA2)
 IND-CCA2 and NM-CCA2 are strictly
equivalent notions.
Notions of Security(3/3)
Random Oracle Model
 Hash functions are considered to be
ideal. i.e. perfect random.
 From a security viewpoint, this
impacts by giving the attacker an
additional access to the random
oracles of the scheme.
Outline







Background
Notation and math. assumption
Scheme 1
Scheme 2
Scheme 3
Properties
Conclusion
Scheme 1(1/4)
 New probabilistic encryption scheme
 n  pq and random base g  B

s.t. gcd( L( g mod n ), n)  1
2
(n, g ) as public parameters;
( p, q) (  ) as private pair.
Scheme 1 (2/4)
•
Enc:
plaintext m  n; random number r  n
ciphertext c  g m  r n mod n 2
i.e. c = g (m, r )
(trapdoor function with  as the trapdoor secret,
one-wayness iff Class[n] hold)
• Dec:
ciphertext c  n 2
L(c  mod n 2 )
plaintext m 
mod n

2
L( g mod n )
u  Sn , L(u ) 
u 1
is clearly well-defined.
n
Scheme 1 (3/4)
 One-way function
 Given x, to compute f(x) = y is easy.
 Given y, to find x s.t. f(x) = y is hard.
 One-way trapdoor
 f() is a one-way function.
 Given a secret s, given y, to find x s.t. f(x) = y is
easy.
 Trapdoor permutation
 f() is a one-way trapdoor.
 f() is bijective.
Scheme 1 (4/4)
• For example:
n  5*7  35; n 2  1225
 (n)  4*6  24;  (n)  lcm(4,6)  12
Take g  13 s.t. gcd( L(1312 mod 1225),35)  1
Let m  23, r  19
Enc: c  1323 1935 mod 1225  53
L(5312 mod 1225)
Dec: m 
mod 35
12
L(13 mod 1225)
24
=
mod 35
33
u 1
-1

u

S
,
L
(
u
)

is clearly well-defined.
n
=24  33 mod 35
n
=23
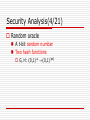
Security Analysis(1/21)
 Against an adaptive chosenciphertext attack.(IND-CCA2)
 In the scenario, the adversary makes
of queries of her choice to a
decryption oracle during two stages.
Security Analysis(2/21)
 The first stage, the find stage
 Attacker chooses two messages.
 Requests encryption oracle to encrypted
one of them.
 the encryption oracle makes the secret
choice of which one.
Security Analysis(3/21)
 The second stage, the guess stage
 To query the decryption oracle with
ciphertext of her choice.
 Finally, she tell her guess about the
choice the encryption oracle made.
Security Analysis(4/21)
 Random oracle
 A t-bit random number
 Two hash functions
 G, H: {0,1}* →{0,1}|n|
Security Analysis(5/21)
 Provided t=Ω(|n|δ) for δ>0, Scheme 1 is
semantically secure against adaptive
chosen-ciphertext attacks (IND-CCA2)
under the Decision Composite Residuosity
assumption (D-Class assumption) in the
random oracle.
 D-Class[n]
 decisional Class[n] problem
 given w∈Zn2*,g∈B, x∈Zn, decide whether x=[w]g
or not
Security Analysis(6/21)
 An adversary A=(A1,A2) against
semantic security of scheme 1.
 A1: the find stage
 A2: the guess stage
 This adversary to efficiently decide nth
residuosity classes.
Security Analysis(7/21)
 Oracle G
 Indistinduishability of encryption
 Oracle H
 Adaptive attack
Security Analysis(8/21)
 Simulation of the Decryption Oracle
 The attacker asks for aciphertext c to be
decrypted.
 The simulator checks in the queryhistory from the random oracle H.
 Whether some entry leads to the
ciphertext c and then return m;
otherwise, it return “failure”.
Security Analysis(9/21)
 Quasi-perfect simulation
 The probability of producing a valid
ciphertext without asking the query (m,r)
to the random oracle H (whose answer a
has to satisfy the test an = z mod n) is
upper bounded by 1/ψ(n)≦2/n, which is
clearly negligible.
Security Analysis(10/21)
 Initialization
 n=pq, g∈Zn2*
 Public: n,g
 Private: λ
Security Analysis(11/21)
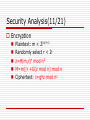
 Encryption





Plaintext: m < 2|n|-t-1
Randomly select r < 2t
z=H(m,r)n mod n2
M=m||r +G(z mod n) mod n
Ciphertext: c=gMz mod n2
Security Analysis(12/21)
 Decryption
Ciphertext: c=gMz mod n2 ∈Zn2*
M=[L(cλmod n2)/L(gλmod n2)] mod n
z’=g-Mc mod n
m’||r’=M-G(z’) mod n
If H(m’,r’)n = z’ mod n, then the plaintext
is m’
 Otherwise, output “failure”





Security Analysis(13/21)
 Attacker A to design a distinguisher B
for nth residuosity class.
 (w,α) is a instance of the D-Class
problem, where α is the nth
residuosity class of w.
 D-Class[n]
 decisional Class[n] problem
 given w∈Zn2*,g∈B, α∈Zn, decide whether
α=[w]g or not
Security Analysis(14/21)
 Distinguisher B(1/2)
 Randomly chooses u∈Zn, v∈Zn*, 0≦r<2t.
 Compute the follows
 z=wg-αvn mod n
 c=wguvn mod n2
 Run A1 and gets two messages m0,m1
Security Analysis(15/21)
 Distinguisher B(2/2)
 Chooses a bit b
 Run A2 on the ciphertext c, supposed to
the ciphertext of mb and using the
random r.
Security Analysis(16/21)
 Shut this game down
 z is asked to the oracle G, shut this
game down and B return 1.
 This event will be denote by AskG
 If (m0,r) or (m1,r) are asked to the
oracle H, shut this geme down and B
return 0.
 This event will be denote by AskH
 In any other case, B return 0 when A2
end.
Security Analysis(17/21)
 One event AskG or AskH is likely to
happen, B terminate the game.
 The random choice of r,
Pr[AskH]=O(qH/2t) in any case,
qH=#(queries asked to the oracle H)
and 0≦r<2t.
 G and H are seen like random oracles,
the attacker has no chance to
correctly guess b, during a real attack.
Security Analysis(18/21)
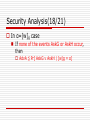
 In α=[w]g case
 If none of the events AskG or AskH occur,
then
 AdvA ≦ Pr[ AskG ∨ AskH | [w]g = α]
Security Analysis(19/21)
 In α≠[w]g case
 z is perfectly random (independent of c),
then Pr[AskG] ≦ qG/ψ(n), qG=#(queries
asked to the oracle G) and u∈Zn, v∈Zn*,
z=wg-αvn mod n
Security Analysis(20/21)
• The advantage of distinguisher B in deciding
the nth residuosity classes:
AdvB
 Pr[1|[ w]g   ]  Pr[1|[ w]g   ]
 Pr[ AskG |[ w]g   ]  Pr[ AskG |[ w]g   ]
 Pr[ AskG  AskH |[ w]g   ]  Pr[ AskH |[ w]g   ]  Pr[ AskG |[ w]g   ]
qH qG
 AdvA  t 
2  ( n)
qH 2qG
 AdvA  t 
2
n
Security Analysis(21/21)
• Reduction Cost
– If there exists an active attacker A against semantic
security, one can decide nth residuosity classes with
an advantage greater then
2 qD qH 2qG
AdvA  (1  )  t 
n
2
n
qG  qD
qH
 AdvA  t  2
2
n