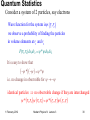Download ModPhys IV Lecture 3

Fromm Institute for Lifelong Learning
University of San Francisco
Modern Physics for Frommies IV
The Universe - Small to Large
Lecture 3
1 February 2012
Modern Physics IV Lecture 3
1
Agenda
• Administrative Matters
• Atomic Physics
• Molecules
Administrative Matters
• This is Lecture 3, Lecture 8 will be Wed. 7 March
• Wikis from previous course
http://modphysicsfrommiies.wiki.usfca.edu/
Note the ii in frommiis
http://modphysfromm2.wiki.usfca.edu
http://modphysfromm3.wiki.usfca.edu
The current course wiki, http://modphysfromm4.wiki.usfca.edu , now
includes a Glossary of Mathematical Symbols,
Other glossaries can be found on Google by searching “mathematics
symbols”
Quantum Mechanical View of Atoms
Bohr model discarded as an accurate description of nature
Certain aspects have however been retained
e.g.
Electrons in an atom exist only in discrete states of
definite energy, the stationary states
Transitions between these states require the emission (or
absorption of a photon.
According to wave mechanics, electrons do not travel in well
defined circular orbits ala Bohr. The electron, because of its
wave nature, is better thought of as spread out in space as a
“cloud”.
The size and shape of the electron cloud can be found by
solving the Schrödinger equation for the atom and forming
the probability distribution, |y |2.
1 February 2012
Modern Physics IV Lecture 3
4
Ground state of hydrogen
1 February 2012
Modern Physics IV Lecture 3
5
Schrödinger’s Equation in Spherical Coordinates
z
In Cartesian coordinates

r

y
2
2m
 2y ( x, y, z )  Ey  x, y, z 
2
2
2



 
2
where    2  2  2 
z 
 x y
x
Separation of variables:
Assume a solution of the form y  x, y, z   X  x  Y  y  Z  z 
1 February 2012
Modern Physics IV Lecture 3
6
Want to do the same thing with spherical symmetry
1 February 2012
Modern Physics IV Lecture 3
7
Spherical Time Independent Schrödinger Equation
1   2 y 
1
 
y 
1
 2y 2m
 2  E  V y  0
r
 2
 sin 
 2 2
2
2
r r  r  r sin   
  r sin  
1 e2
where for the hydrogen atom V 
4 0 r
Separation of variables:
y  r, ,    R  r       
Try solution of form
y (r, , )  R  r  Yl  ,  
spherical harmonics: Yl m  ,    Pl m  cos   eim 
l
n
m
l
l
where the Pl m are associated Legendre polynomials
associated LaGuerre functions: Rnl  r 
1 February 2012
Modern Physics IV Lecture 3
8
Quantum Numbers
If we do QM in for a particle confined in a 1-D and 3-D potential
well or rigid box. (See Course II Lecture 4)
The solutions are characterized by a single quantum number (n)
in the 1-D case and by three numbers (nx, ny and nz) in 3-D.
These quantum numbers arise from the imposition of
boundary conditions on the solutions. We might expect that
in the 3-D problem of the hydrogen atom the solutions will
be characterized by numbers corresponding to Boundary
conditions applied in 3-D. Restrictions on the values of these
quantum numbers arise from the mathematics of the
LaGuerre functions and the spherical harmonics.
Actually, we need a fourth number. There is an additional
degree of freedom which I will treat in a few minutes.
1 February 2012
Modern Physics IV Lecture 3
9
n  1, 2,3, 
principle quantum number
E0
m  e2  1
En   2   
 2
n
2  4 0  n
Bohr result
Results from boundary conditions on solution of the
R part of the separated Schrödinger eqn.
R part contains the potential energy
n alone determines the energy levels (actually there
is a slight deviation from this)
Consequence of central inverse square force.
1 February 2012
Modern Physics IV Lecture 3
10
l  0,1, 2,3, , n  1
orbital angular momentum quantum number
associated with R  r  and    parts of Sch. eqn.
Classically
L  r  p or L  rmvtangential
 h 
Quantum boundary conditions  L  l  l  1  
 2 
Note disageement with Bohr quantization where
 h 
L  n 
 2 
in particular, the ground state has l  0  L  0
The semiclassical planetary model with
electrons in orbits is not a good one
1 February 2012
Modern Physics IV Lecture 3
11
Note: All these
transitions have Dl = 1
1 February 2012
Modern Physics IV Lecture 3
12
s
l=0
p
1
d
2
f
3
g
4
h
5
etc.
etc.
Notation for states: nl, e.g. 4d is n=4, l=2
ml  l , l  1, ,0,1, , l  1, l
magnetic quantum number
L is a vector quantity, conserved in a central potential
The solution for    specifies that ml is an integer related to
L's z -component.
 h 
Lz  ml  
 2 
1 February 2012
Modern Physics IV Lecture 3
13
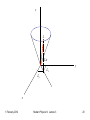
Aside on Angular Momentum
Particle of mass m moving with circular
speed v around an axis at radius r.
L  r  mv

r
v
Magnitude: L  mvr sin 
Here,   90  sin   1  L  mvr
Direction:  to plane of r and v with sense
determined by right hand rule.
1 February 2012
Modern Physics IV Lecture 3
14
C  A B
C  AB sin 
 To the plane of AB
C
Right Hand Rule
A
Direction of advance of a
right hand screw
1 February 2012
Modern Physics IV Lecture 3
15
C  A B
Note that the vector product is not commutative
A  B  B  A
Again look at Right Hand Rule
C
A×B
‛A
B×A
1 February 2012
Modern Physics IV Lecture 3
16
L  l  l  1
fixed
Lz  ml
restricted
Note choice of z axis is
arbitrary.
Space quantization
1 February 2012
Modern Physics IV Lecture 3
17
Energy is dependent solely on n.
Presence of multiple ls and ms for a given n

states are degenerate
This degeneracy is removed if directional symmetry
is broken by say a B or E field.
What about Lx and Ly?
1 February 2012
Modern Physics IV Lecture 3
18
If L and Lz are known, knowledge of 2nd component
 3rd is also known.
consequence of L2  L2x  L2y  L2z
Uncertainty principle: DLz D 
If we know Lz exactly, we know nothing of 
 we know nothing of Lx and Ly
1 February 2012
Modern Physics IV Lecture 3
19
z
L
Liz
Lx
y
Ly
x
1 February 2012
Modern Physics IV Lecture 3
20
Magnetic effects
Normal Zeeman effect: Transition between 1s and 2p
Spectral lines broaden and split into 3 lines as B is
applied and increased. 3 lines = “normal Zeeman effect”
Consider the electron “orbit” to be a current loop with
m  IA
2

e

r


q
m  IA  A 
erv
e


L
T
2 r v
2
2m
e
Vector: m  
L
2m
1 February 2012
Modern Physics IV Lecture 3
21
Apply external magnetic field
Torque: N  m  B
Potential energy: U B   m  B
e
mz 
ml  m B ml
2m
e
mB 
 Bohr magneton
2m
1 February 2012
Modern Physics IV Lecture 3
22
L quantized  m quantized
Additional potential energy term:
U B   m z B   m B ml B
Each degenerate energy level, l, is split into 2l+1
separate energy levels, ml.
B has specified a direction in space (z axis) and the
symmetry responsible for the degeneracy has been
broken.
1 February 2012
Modern Physics IV Lecture 3
23
The Stern-Gerlach experiment:
If B is inhomogeneous there will be a net force as well
as torque on the atom
1 February 2012
Modern Physics IV Lecture 3
24
For l  0 the states should separate according to ml
2 lines seen instead of the expected 3 (or 2l+1 = odd)
Haven’t seen the whole picture yet.
1 February 2012
Modern Physics IV Lecture 3
25
Electron Spin
Wolfgang Pauli:
Relativity  besides n, l, ml need 4th quantum number
G. Hollenbeck and S. Goudsmit:
Propose intrinsic “spin” angular momentum for the electron
s = ½ħ
Another magnetic quantum number: ms =  ½
1928, P. A. M. Dirac justifies this from relativity.
i  y  my
1 February 2012
Modern Physics IV Lecture 3
26
Gives magnetic effects like orbital angular momentum.
Intrinsic spin → intrinsic magnetic dipole moment
New magnetic quantum numbers:
ms = ± 1/2
Doubles number of states for a given n
States are degenerate unless a spatial direction is
specified, e.g. external E or B field
Quantum state now specified by {n, l, ml, ms}
1 February 2012
Modern Physics IV Lecture 3
27
Return to the Stern-Gerlach experiment
l = 0 state will give 2 lines for ms = ± 1/2
Fine structure:
Even in the absence of external fields, very high resolution
spectroscopy reveals splitting of spectral lines.
Rest frame of electron: nucleus orbits and appears as a current
loop. Interacts with spin magnetic moment and breaks
degeneracy
Line separation is about 5 x 10-5 eV compared to the 2p  1s
transition energy of 10.2 eV
Hyperfine structure:
Arises from the spin angular momentum and consequent spin
magnetism of the nucleon(s)
1 February 2012
Modern Physics IV Lecture 3
28
s-wave states are spherically symmetric, not so for l  0
1 February 2012
Modern Physics IV Lecture 3
29
Quantum Statistics
Consider a system of 2 particles, say electrons
Wave function for the system isy  r1 , r2 
we observe a probability of finding the particles
in volume elements at r1 and r2
P(r1 , r2 )dv1dv2  y *y dv1dv2
It is easy to show that
 y * y   y *y
i.e. no change in observable for y  y
identical particles  no observable change if they are interchanged
y *  r1 , r2 y  r1 , r2   y *  r2 , r1 y  r2 , r1 
1 February 2012
Modern Physics IV Lecture 3
30
So, under interchange  2 possibilities
y  ±y
If 2 identical particles interchange  y = +y, they are
said to obey Bose-Einstein statistics and are called
bosons.
If 2 identical particles interchange  y = -y, they are
said to obey Fermi-Dirac statistics and are called
fermions.
Bosons have integral spin, e.g. photons, mesons, some
atoms and nuclei, ………
1 February 2012
Modern Physics IV Lecture 3
31
Fermions have ½ integral spin, e.g. leptons, nucleons,
some atoms and nuclei,………..
For fermions y  y > y  0
> Cannot have 2 identical particles with the same
set of quantum numbers.
Pauli Exclusion Principle
You can stick as many bosons into a quantum state
as you want.
1 February 2012
Modern Physics IV Lecture 3
32
Electrons are fermions.
Build some elements. As electrons are added the
exclusion principle will have an effect.
Hydrogen: 1 e in the 1s state
1s1
He: 2 e in the 1s state, ms =1 and -1,
1s2
No more e can be added to the 1s state without
violating the exclusion principle !
The K shell is filled
1 February 2012
Modern Physics IV Lecture 3
33
Li: 3rd e has to go in 2s state
2s1
Be: 4th e in the 2s state, ms =1 and -1,
2s2
2s state (subshell) is now filled
B: 5th e has to go in the 2p state
2p1
p state has 2l+1 = 3 values of ml, each with 2 values
of ms, accommodating C, N, O, F and Ne as 2p2 – 2p6.
2p subshell is now filled, as is the L shell
Na: 11th e has to go in 3s state
1 February 2012
Modern Physics IV Lecture 3
3s1
etc.
34
3s and 3p each with 2l+1 ml values each having 2
values of ms.
Weirdoes:
3d, 4d and 5d subshells fill up the transition metals
followed by the lanthanides and the actinides
Complicated inter electron interactions mess things up
If electrons were bosons, they would all sit in the ground
state, 1s, and chemistry would be very different.
1 February 2012
Modern Physics IV Lecture 3
35
1 February 2012
Modern Physics IV Lecture 3
36
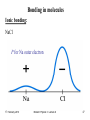
Bonding in molecules
Ionic bonding:
NaCl
P for Na outer electron
17 February 2010
Modern Physics II Lecture 6
37
Na has 11 e-
Na
10 reside in inner closed shells
Last e- spends most of its time
outside these shells.
The last e- feels net attraction due to +1e, not all that strong
Cl has 17 e-
Cl
12 are in closed shells
1s22s22p63s2
Others are in non spherically
symmetric p states
17 February 2010
Modern Physics II Lecture 6
38
Exclusion principle
allows one more e- in
ml = 0 with spin
oriented opposite to
that of the last Cl e-
H
ml=0, unpaired
4 states ml=±1, ms=±1
If an extra electron happens to be in the vicinity it can
be in this state and could see an attraction due to Cl
nucleus as much as +5e.
Stronger than the +1e attraction between Na nucleus
and its outer electron  charge distribution in slide
#36 and an ionic bond between Na and Cl.
17 February 2012
Modern Physics II Lecture 6
39
Covalent bonding:
If H atoms are close together, e- clouds
H+H  H2
overlap and e- “orbit” both nuclei.
Both H s in ground state. Electron spins can be
either parallel (S = 1) or antiparallel (S = 0)
1st consider S = 1:
Exclusion principle  2 e- with
same quantum numbers must be
in different places, i.e. belong to
different atoms.
(+) nuclei repel, no bond is
formed.
17 February 2010
Modern Physics II Lecture 6
40
S = 0:
e- have different values for ms, spend
a lot of time in the internuclear
region
(+) nuclei are attracted to the
internuclear e- and a bond is
formed.
In a wave picture, exclusion principle  destructive
interference when S=1 and constructive when S=0.
17 February 2012
Modern Physics II Lecture 6
41
Energetics point of view:
For S = 0, e- can occupy same space, space of 2 atoms
rather than 1  Dx is increased.
H. U. P  Dp can be less  energy is less
Molecule has lower energy than the 2 separate atoms
 H2 is stable
Binding energy is 4.5 eV for H2
17 February 2012
Modern Physics II Lecture 6
42
In the vicinity of r0 we may
approximate
0.074 nm
17 February 2010
A B
 n
m
r
r
A, B constants for attractive,
repulsive parts of U
m, n are small integers
U 
Modern Physics II Lecture 6
43
Activation energy often  need to break earlier bonds
2 H2 + O2  2H2 O
H 2 and O2 must 1st be broken into H and O atoms
spark
UA = 0 for hypergolic materials, don’t need spark
17 February 2012
Modern Physics II Lecture 6
44
Energy storage in
biological systems
adenosine triphosphate
ATP  ADP + (phosphate group) + ENERGY
17 February 2012
Modern Physics II Lecture 6
45