Download x + 2 - hendrymath9

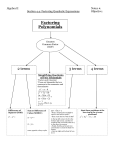
Factoring Trinomials
• Remember: Factoring is the opposite of expanding
Ex.
(x+3)(x+2) = x2 + 5x + 6
• Trinomial – 3 terms.
• The factors of a trinomial will be two binomials.
Let’s take a Look
y2 + 3y + 2
Middle Term: Sum of 3
Last Term: Product of 2
Consider:
Consider:
What two
numbers add
up to +3?
The same two
numbers
must multiply
to give you +2
( 2 and 1 )
Therefore: y2 + 3y + 2
= (y + 1)(y + 2)
Factors:
Options: 1 and 2
Let’s take a Look
g2 – 4g + 3
How can we check
our answer?
Let’s take a Look
x2 – 7x + 12
Chart to Help with Signs
Sum
(• 2nd Term)
Negative
Product
( 3rd Term)
Negative
Negative
Positive
Positive
Negative
Positive
Positive
INTEGERS
Bigger #(-)
Smaller # (+)
Both Negative
numbers
Bigger # (+)
Smaller # (-)
Both Numbers
Positive
x2 + 6x + 8
Middle Term: Sum of 6
Last Term: Product of 8
What two
numbers add
up to + 6
Same two
numbers that
multiply to
give you 8
Therefore:
x2
= (x
)
)(x
+ 6x + 8
Factors:
Options:
Which gives a sum of +6?
x2 + 6x + 8
Middle Term: Sum of 6
Last Term: Product of 8
What two
numbers add
up to + 6
Same two
numbers that
multiply to
give you 8
Factors:
Options: 1 x 8 or -1 x -8
2 x 4 or -2 x -4
Which gives a sum of +6?
Therefore:
x2
+ 6x + 8
= (x + 2)(x + 4)
(2 and 4)
x2 + 2x - 15
Middle Term: Sum of 2
Last Term: Product of -15
What two
numbers add
up to + 2
Same two
numbers that
multiply to
give you -15
Therefore:
x2
= (x
)
)(x
+ 2x - 15
Factors:
Options:
Which gives a sum of +2?
x2 + 2x - 15
Middle Term: Sum of 2
Last Term: Product of -15
What two
numbers add
up to + 2
Same two
numbers that
multiply to
give you -15
Factors:
Options: 1 x 15 or -1 x -15
3 x 5 or -3 x -5
Which gives a sum of +2?
Therefore:
x2
= (x -3)(x + 5)
+ 2x - 15
-3 and +5
(use chart to help with signs)
y2 - 4y - 12
Middle Term: Sum of - 4
Last Term: Product of -12
What two
numbers add
up to - 4
Same two
numbers that
multiply to
give you - 12
Therefore:
y2
= (y
)
)(y
– 4y - 12
Factors:
Options:
Which gives a sum of - 4?
y2 - 4y - 12
Middle Term: Sum of - 4
Last Term: Product of -12
What two
numbers add
up to - 4
Same two
numbers that
multiply to
give you - 12
Factors:
Options: 1 x 12 or -1 x -12
2 x 6 or -2 x -6
3 x 4 or -3 x -4
Therefore:
y2
– 4y - 12
= (y - 6)(y + 2)
Which gives a sum of - 4?
- 6 and + 2
y2 - 5y + 4
Middle Term: Sum of - 5
Last Term: Product of + 4
What two
numbers add
up to - 5
Same two
numbers that
multiply to
give you + 4
Therefore:
y2
= (y
)
)(y
– 5y + 4
Factors:
Options:
Which gives a sum of - 5?
y2 - 5y + 4
Factors:
Middle Term: Sum of - 5
What two
numbers add
up to - 5
Same two
numbers that
multiply to
give you + 4
Last Term: Product of + 4
Options: 1 x 4 or -1 x -4
2 x 2 or - 2 x -2
Which gives a sum of - 5?
Therefore:
y2
= (y -1)(y - 4)
– 5y + 4
-1 and - 4
Class work
• Please complete worksheet “Factoring
Trinomials” (Lesson 3-10a)