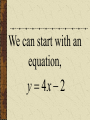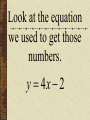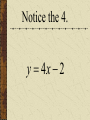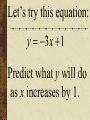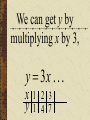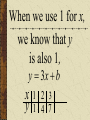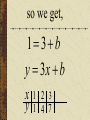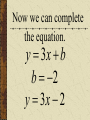Download Arithmetic and Geometric Sequence Instructional PowerPoint

Patterns and Sequences
Patterns and Sequences
Patterns refer to usual types of procedures or rules that can be
followed.
Patterns are useful to predict what came before or what might
come after a set a numbers that are arranged in a particular order.
This arrangement of numbers is called a sequence.
For example:
3,6,9,12 and 15 are numbers that form a pattern called a sequence
The numbers that are in the sequence are called terms.
Patterns and Sequences
Arithmetic sequence (arithmetic
progression) – A sequence of numbers in
which the difference between any two
consecutive numbers or expressions is the
same.
Geometric sequence – A sequence of
numbers in which each term is formed by
multiplying the previous term by the same
number or expression.
Arithmetic Sequence
Find the next three numbers or terms in each pattern.
a. 7, 12, 17, 22,...
a. 7, 12, 17, 22,...
5
5
5
Look for a pattern: usually a procedure or rule that uses the
same number or expression each time to find the next term.
The pattern is to add 5 to each term.
The next three terms are:
22  5  27
27  5  32
32  5  37
a. 7, 12, 17, 22,...
27,32,37
Arithmetic Sequence
Find the next three numbers or terms in each pattern.
b. 45, 42, 39, 36,...
b. 45, 42, 39, 36,...
 (3)
 (3)
 (3)
Look for a pattern: usually a procedure or rule that uses the
same number or expression each time to find the next term.
The pattern is to add the integer (-3) to each term.
The next three terms are:
b. 45, 42, 39, 36,...
36  (3)  33
33  (3)  30
30  (3)  27
33,30,27
Geometric Sequence
Find the next three numbers or terms in each pattern.
b. 3, 9, 27, 81,...
b. 3, 9, 27, 81,...
3
3
3
Look for a pattern: usually a procedure or rule that uses the
same number or expression each time to find the next term.
The pattern is to multiply 3 to each term.
The next three terms are:
b. 45, 42, 39, 36,...
81
1
2
3
243
243
3
729
729
3
2187
33,30,27
Geometric Sequence
Find the next three numbers or terms in each pattern.
b. 528, 256, 128, 64... b. 528, 256, 128, 64,...
Look for a pattern: usually a
procedure or rule that uses the same
number or expression each time to
find the next term. The pattern is to
divide by 2 to each term.
The next three terms are:
64  2  32
or
64 1 64
 
 32
1 2 2
16  2  8
or
16 1 16
  8
1 2 2
1
 2 or 
2
 2 or 
1
1
2  2 or  2
Note: To divide by a number is the same
as multiplying by its reciprocal. The
pattern for a geometric sequence is
represented as a multiplication pattern.
For example: to divide by 2 is
represented as the pattern multiply by ½.
b. 528, 256, 128, 64,...
32  2  16
or
32 1 32
 
 16
1 2 2
32,16,8
We can start with an
equation,
y  4x  2
and see what pattern
develops.
y  4x  2
x1 2 3
y 2 6 10
What happens to y each time x
increases by 1?
Remember that slope (m) = change in y
change in x
x1 2 3
y 2 6 10
Change in x = 1
Change in y = 4
Slope of this table is 4/1
=4
Each time x increases by 1 y
increases by 4
x1 2 3
y 2 6 10
Look at the equation
we used to get those
numbers.
y  4x  2
Notice the 4.
y  4x  2
Let’s try this equation:
y  3x  1
Predict what y will do
as x increases by 1.
y  3x  1
x
y
1 2 3
?2 ?5 ?8
There is a pattern
working here.
is part of the equation.
1So if w go back to the
...
pattern we started with:
x
y
1 2 3
1 4 7
We see that y
increases by 3 each
time x increases by 1,
and we can start
writing the equation.
We can get y by
multiplying x by 3,
y  3x . . .
x
y
1 2 3
1 4 7
and then adding or
subtracting some
number.
y  3x
. .b.
3x 
x
y
1 2 3
1 4 7
When we use 1 for x,
we know that y
is also 1,
y  3x  b
x
y
1 2 3
1 4 7
so we get,
1 3b
y  3x  b
x
y
1 2 3
1 4 7
What does b have to be to make the
equation true?
1 3b
y  3x  b
x
y
1 2 3
1 4 7
Another way to find b is to
understand the table of
values
X
1
2
3
Y
1
4
7
The first term in the table (where x=1) shows a value of y = 1
The second term in the table (where x=2) shows a value of y = 4
The third term in the table (where x=3) shows a value of y = 7
You may recall that at the y-intercept (“b”) x = 0; therefore, the
zero term in the table (where x=0) would show a value of y = -2
since the pattern (or change in y is to +3)
Now we can complete
the equation.
y  3x  b
b  2
y  3x  2