Elementary Problems and Solutions
... So: A Monotonic Surjection from Z+ to Z+, 8.1(1970)111 To:Some Fibonacci-Lucas identities, 7.3(1969)331 So: Generalizations of Second-Order Recurrences, 8.3(1970)326 To:Lucas inequality, 7.3(1969)331 So: A Lucas Inequality, 8.3(1970)328 To:Multiples of a six digit number, 7.3(1969)331 So: An Applica ...
... So: A Monotonic Surjection from Z+ to Z+, 8.1(1970)111 To:Some Fibonacci-Lucas identities, 7.3(1969)331 So: Generalizations of Second-Order Recurrences, 8.3(1970)326 To:Lucas inequality, 7.3(1969)331 So: A Lucas Inequality, 8.3(1970)328 To:Multiples of a six digit number, 7.3(1969)331 So: An Applica ...
Advanced Problems and Solutions
... [Reference to special case], 3.2(1965)123 Generalized Fibonacci numbers, 2.3(1964)205 A Favorable Response, 3.2(1965)123 Quadruple sums of Fibonacci squares, 2.3(1964)205 Iterated Sums of Squares, 3.2(1965)127 Determinant with Fibonacci fourth power elements, 2.4(1964)303 Problems and Papers; [Annou ...
... [Reference to special case], 3.2(1965)123 Generalized Fibonacci numbers, 2.3(1964)205 A Favorable Response, 3.2(1965)123 Quadruple sums of Fibonacci squares, 2.3(1964)205 Iterated Sums of Squares, 3.2(1965)127 Determinant with Fibonacci fourth power elements, 2.4(1964)303 Problems and Papers; [Annou ...
Full text
... numbers will be the first n Fibonacci numbers. Koh, Lee, & Tan gave a systematic way to obtain all Fibonacci trees as subgraphs of a certain class of graphs and showed that the number of (labeled) Fibonacci trees on n + 1 vertices is equal to Fn . The only graphs other than trees which can be labele ...
... numbers will be the first n Fibonacci numbers. Koh, Lee, & Tan gave a systematic way to obtain all Fibonacci trees as subgraphs of a certain class of graphs and showed that the number of (labeled) Fibonacci trees on n + 1 vertices is equal to Fn . The only graphs other than trees which can be labele ...
Fibonacci Sequences of Higher Order!
... 21, 34. This sequence is a list of numbers in which the last two numbers are summed to yield the next one, starting at the number one. Leonardo Pisano Bigollo created the list of numbers in his famous book, Liber Abaci, in which he tried to explain the pattern of rabbit population growth. In this ma ...
... 21, 34. This sequence is a list of numbers in which the last two numbers are summed to yield the next one, starting at the number one. Leonardo Pisano Bigollo created the list of numbers in his famous book, Liber Abaci, in which he tried to explain the pattern of rabbit population growth. In this ma ...
Fibonacci numbers
... Fibonacci primes Main article: Fibonacci prime A Fibonacci prime is a Fibonacci number that is prime. The first few are: 2, 3, 5, 13, 89, 233, 1597, 28657, 514229, … (sequence A005478 in OEIS). Fibonacci primes with thousands of digits have been found, but it is not known whether there are infinitel ...
... Fibonacci primes Main article: Fibonacci prime A Fibonacci prime is a Fibonacci number that is prime. The first few are: 2, 3, 5, 13, 89, 233, 1597, 28657, 514229, … (sequence A005478 in OEIS). Fibonacci primes with thousands of digits have been found, but it is not known whether there are infinitel ...
Full text
... line of reasoning, it is possible to prove that there are general principles in pattern formation on the plants. 69 CONCLUSIONS In this paper we have presented the new ideas and concepts concerning hyperbolic trigonometry. It has been shown that many problems appearing in mathematical modeling of ph ...
... line of reasoning, it is possible to prove that there are general principles in pattern formation on the plants. 69 CONCLUSIONS In this paper we have presented the new ideas and concepts concerning hyperbolic trigonometry. It has been shown that many problems appearing in mathematical modeling of ph ...
Proof of Infinite Number of Fibonacci Primes Stephen
... is also prime. Since we proved earlier that if Fy-1 + Fy-2 is prime then it also is not in the finite set of pi Fibonacci primes, therefore, since we have proven that Fy-1 + Fy-2 = Fy is prime, then we have proven that there is a Fibonacci prime outside our assumed finite set of Fibonacci primes. Th ...
... is also prime. Since we proved earlier that if Fy-1 + Fy-2 is prime then it also is not in the finite set of pi Fibonacci primes, therefore, since we have proven that Fy-1 + Fy-2 = Fy is prime, then we have proven that there is a Fibonacci prime outside our assumed finite set of Fibonacci primes. Th ...
Contents - The Sound of Numbers
... (1709) is a good example. In the excerpt that begins this chapter, he ridicules critics who judge poetry “by numbers”—that is, solely on how well a poet follows strict metrical rules. While English poets use relatively few meters, there are hundreds of different meters in Sanskrit, the classical lan ...
... (1709) is a good example. In the excerpt that begins this chapter, he ridicules critics who judge poetry “by numbers”—that is, solely on how well a poet follows strict metrical rules. While English poets use relatively few meters, there are hundreds of different meters in Sanskrit, the classical lan ...
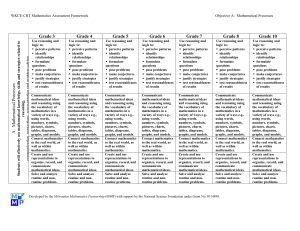
Algebraic Relationships
... students by writing for them until they have the ability to record their ideas. Original representations remain important throughout the students’ mathematical study and should be encouraged. Symbolic representations and manipulation should be embedded in instructional experiences as another vehicle ...
... students by writing for them until they have the ability to record their ideas. Original representations remain important throughout the students’ mathematical study and should be encouraged. Symbolic representations and manipulation should be embedded in instructional experiences as another vehicle ...
the existence of fibonacci numbers in the algorithmic generator for
... delve more deeply into the mathematical world. He is best known for the sequence of numbers bearing his name. Leonardo Pisano Bigollo (c. 1170 – c. 1250) [Wikipedia) – known as Fibonacci, and also Leonardo of Pisa, Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci – was an Italian mathematician, ...
... delve more deeply into the mathematical world. He is best known for the sequence of numbers bearing his name. Leonardo Pisano Bigollo (c. 1170 – c. 1250) [Wikipedia) – known as Fibonacci, and also Leonardo of Pisa, Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci – was an Italian mathematician, ...
“How to use Fibonacci retracement to predict forex market”
... are created also with Fibonacci retracement and also rules to perfect chart plotting. I have analyzed some examples of Fibonacci retracements pattern in a downtrend and in an uptrend. In this article I have used and combine material from different sources trying to create a start point for those one ...
... are created also with Fibonacci retracement and also rules to perfect chart plotting. I have analyzed some examples of Fibonacci retracements pattern in a downtrend and in an uptrend. In this article I have used and combine material from different sources trying to create a start point for those one ...
Three - Faculty Web Pages
... Sicily, and Provence, where he not only conducted business but also met with mathematicians to learn their ways of doing mathematics. Indeed Fibonacci sometimes referred to himself as “Bigollo,” which could mean good-for-nothing or, more positively, traveler. He may have liked the double meaning. Wh ...
... Sicily, and Provence, where he not only conducted business but also met with mathematicians to learn their ways of doing mathematics. Indeed Fibonacci sometimes referred to himself as “Bigollo,” which could mean good-for-nothing or, more positively, traveler. He may have liked the double meaning. Wh ...
Introduction to logarithms
... part of plot, and these parts has comparable size. If the x axis would be linear instead of logarithmic, the main part of it would be occupied by frequency response of tweeter alone, because it has widest frequency range. While bass speaker has narrowest frequency range, it would have very thin part ...
... part of plot, and these parts has comparable size. If the x axis would be linear instead of logarithmic, the main part of it would be occupied by frequency response of tweeter alone, because it has widest frequency range. While bass speaker has narrowest frequency range, it would have very thin part ...
13 SEQUENCES
... Neptune was the first planet to be found by mathematical prediction. It was found by looking at the number patterns of the other planets in the Solar System, and its position was correctly predicted to within a degree. Two scientists were eventually jointly credited with the discovery, one British a ...
... Neptune was the first planet to be found by mathematical prediction. It was found by looking at the number patterns of the other planets in the Solar System, and its position was correctly predicted to within a degree. Two scientists were eventually jointly credited with the discovery, one British a ...
Sequences - Pearson Schools and FE Colleges
... Neptune was the first planet to be found by mathematical prediction. It was found by looking at the number patterns of the other planets in the Solar System, and its position was correctly predicted to within a degree. Two scientists were eventually jointly credited with the discovery, one British a ...
... Neptune was the first planet to be found by mathematical prediction. It was found by looking at the number patterns of the other planets in the Solar System, and its position was correctly predicted to within a degree. Two scientists were eventually jointly credited with the discovery, one British a ...
Foundation Student Book Chapter 13 - Sequences
... Neptune was the first planet to be found by mathematical prediction. It was found by looking at the number patterns of the other planets in the Solar System, and its position was correctly predicted to within a degree. Two scientists were eventually jointly credited with the discovery, one British a ...
... Neptune was the first planet to be found by mathematical prediction. It was found by looking at the number patterns of the other planets in the Solar System, and its position was correctly predicted to within a degree. Two scientists were eventually jointly credited with the discovery, one British a ...
FIBONACCI - HIS RABBITS AND HIS NUMBERS and KEPLER
... Leonardo of Pisa (of leaning tower fame), better known to us as Fibonacci, was born about 1175 and died about 1250. His fame rests mainly on his book Liber Abacci (A Book about the abacus or, the book of calculations - in fact its objective was to make the abacus obsolete) which he wrote in 1202. A ...
... Leonardo of Pisa (of leaning tower fame), better known to us as Fibonacci, was born about 1175 and died about 1250. His fame rests mainly on his book Liber Abacci (A Book about the abacus or, the book of calculations - in fact its objective was to make the abacus obsolete) which he wrote in 1202. A ...
Recent progress in additive prime number theory
... Arithmetic progressions are more “indestructible” than other patterns. ...
... Arithmetic progressions are more “indestructible” than other patterns. ...
Conjecture
... 2. Find mC if C and D are supplementary, mC = 3y – 5, and mD = 8y + 20. 5. The midpoint of AB is (3, –2). The coordinates of A are (7, –1). What are the coordinates of B? ...
... 2. Find mC if C and D are supplementary, mC = 3y – 5, and mD = 8y + 20. 5. The midpoint of AB is (3, –2). The coordinates of A are (7, –1). What are the coordinates of B? ...
- The Sound of Numbers
... and accents that identify different styles of dance music, such as ska and reggae. Listen to the audio, starting around 3:00, in which James Brown, “The Godfather of Soul,” discusses grooves in his music in this 2005 interview with Terry Gross of NPR. He compares two versions of the “I Got You” groo ...
... and accents that identify different styles of dance music, such as ska and reggae. Listen to the audio, starting around 3:00, in which James Brown, “The Godfather of Soul,” discusses grooves in his music in this 2005 interview with Terry Gross of NPR. He compares two versions of the “I Got You” groo ...
ppt - School of Computer Science
... Church and Turing were both interested in the number of whorls in each ring of the spiral. The ratio of consecutive ring lengths approaches the Golden Ratio. ...
... Church and Turing were both interested in the number of whorls in each ring of the spiral. The ratio of consecutive ring lengths approaches the Golden Ratio. ...
Patterns & Algebra 1
... Paul visits the library every fourth day in January (beginning on January 4th). Werda visits every sixth day (beginning on January 6th). Nigel visits every 8th day (beginning on January 8th). On what day of the month will they all visit the library together? ...
... Paul visits the library every fourth day in January (beginning on January 4th). Werda visits every sixth day (beginning on January 6th). Nigel visits every 8th day (beginning on January 8th). On what day of the month will they all visit the library together? ...
Patterns in nature

Patterns in nature are visible regularities of form found in the natural world. These patterns recur in different contexts and can sometimes be modelled mathematically. Natural patterns include symmetries, trees, spirals, meanders, waves, foams, tessellations, cracks and stripes. Early Greek philosophers studied pattern, with Plato, Pythagoras and Empedocles attempting to explain order in nature. The modern understanding of visible patterns developed gradually over time.In the 19th century, Belgian physicist Joseph Plateau examined soap films, leading him to formulate the concept of a minimal surface. German biologist and artist Ernst Haeckel painted hundreds of marine organisms to emphasise their symmetry. Scottish biologist D'Arcy Thompson pioneered the study of growth patterns in both plants and animals, showing that simple equations could explain spiral growth. In the 20th century, British mathematician Alan Turing predicted mechanisms of morphogenesis which give rise to patterns of spots and stripes. Hungarian biologist Aristid Lindenmayer and French American mathematician Benoît Mandelbrot showed how the mathematics of fractals could create plant growth patterns.Mathematics, physics and chemistry can explain patterns in nature at different levels. Patterns in living things are explained by the biological processes of natural selection and sexual selection. Studies of pattern formation make use of computer models to simulate a wide range of patterns.