Patterns & Algebra 1
... On Thursday evening, she will be 75 km from home. 1. On Wednesday morning Blair’s campsite is 18 km from Tea Lake. He plans to hike 5 km towards the lake each day. How far from the lake will he be on Friday evening? _______________ ...
... On Thursday evening, she will be 75 km from home. 1. On Wednesday morning Blair’s campsite is 18 km from Tea Lake. He plans to hike 5 km towards the lake each day. How far from the lake will he be on Friday evening? _______________ ...
13 SEQUENCES
... Neptune was the first planet to be found by mathematical prediction. It was found by looking at the number patterns of the other planets in the Solar System, and its position was correctly predicted to within a degree. Two scientists were eventually jointly credited with the discovery, one British a ...
... Neptune was the first planet to be found by mathematical prediction. It was found by looking at the number patterns of the other planets in the Solar System, and its position was correctly predicted to within a degree. Two scientists were eventually jointly credited with the discovery, one British a ...
Sequences - Pearson Schools and FE Colleges
... Neptune was the first planet to be found by mathematical prediction. It was found by looking at the number patterns of the other planets in the Solar System, and its position was correctly predicted to within a degree. Two scientists were eventually jointly credited with the discovery, one British a ...
... Neptune was the first planet to be found by mathematical prediction. It was found by looking at the number patterns of the other planets in the Solar System, and its position was correctly predicted to within a degree. Two scientists were eventually jointly credited with the discovery, one British a ...
Foundation Student Book Chapter 13 - Sequences
... Neptune was the first planet to be found by mathematical prediction. It was found by looking at the number patterns of the other planets in the Solar System, and its position was correctly predicted to within a degree. Two scientists were eventually jointly credited with the discovery, one British a ...
... Neptune was the first planet to be found by mathematical prediction. It was found by looking at the number patterns of the other planets in the Solar System, and its position was correctly predicted to within a degree. Two scientists were eventually jointly credited with the discovery, one British a ...
- The Sound of Numbers
... styles of popular music. It normally refers to characteristic repeating rhythm patterns and accents that identify different styles of dance music, such as ska and reggae. Listen to the audio, starting around 3:00, in which James Brown, “The Godfather of Soul,” discusses grooves in his music in this ...
... styles of popular music. It normally refers to characteristic repeating rhythm patterns and accents that identify different styles of dance music, such as ska and reggae. Listen to the audio, starting around 3:00, in which James Brown, “The Godfather of Soul,” discusses grooves in his music in this ...
Juggling Sequences with Number Theory
... but they also had more progressive aspirations—the solo performer’s juggling routine would be orderly and sequential but perhaps NOT based on the foundation of first 0 balls, then 1, 2, etc. These neo-foundationalists might start at some non-zero number of balls and then increase from there. • Howev ...
... but they also had more progressive aspirations—the solo performer’s juggling routine would be orderly and sequential but perhaps NOT based on the foundation of first 0 balls, then 1, 2, etc. These neo-foundationalists might start at some non-zero number of balls and then increase from there. • Howev ...
Modeling Moiré: Visual Beat Effects in Nature and Optical Metrology
... Modeling Moiré: Visual Beat Effects in Nature and Optical Metrology ...
... Modeling Moiré: Visual Beat Effects in Nature and Optical Metrology ...
Conjecture
... Step 3 Make a conjecture. Answer: The sum of an odd number and an even number is odd. ...
... Step 3 Make a conjecture. Answer: The sum of an odd number and an even number is odd. ...
Example
... A. Write a conjecture that describes the pattern 2, 4, 12, 48, 240. Then use your conjecture to find the next item in the sequence. ...
... A. Write a conjecture that describes the pattern 2, 4, 12, 48, 240. Then use your conjecture to find the next item in the sequence. ...
COUNTING TRIANGLES SOLUTION - Aiming High Teacher Network
... Then ask the learners to work in pairs to find the number of triangles for 2 extra lines. Discuss this as a class. Then ask the leaners to find the number of triangles for 3, 4, 5, and 6 … extra lines and see if they can spot a pattern. Ask learners to explain what they have discovered. ...
... Then ask the learners to work in pairs to find the number of triangles for 2 extra lines. Discuss this as a class. Then ask the leaners to find the number of triangles for 3, 4, 5, and 6 … extra lines and see if they can spot a pattern. Ask learners to explain what they have discovered. ...
Visualization of Rhyme Patterns in Two Sonnet Sequences
... end-rhyme sounds. Each poet utilizes variation within the general pattern of the Petrarchan sonnet as their sequences develop. The end-rhyme patterns in Rossetti’s Monna Innominata are quite consistent across all 14 sonnets, but there is significant variation in the end-rhyme patterns of the sestet ...
... end-rhyme sounds. Each poet utilizes variation within the general pattern of the Petrarchan sonnet as their sequences develop. The end-rhyme patterns in Rossetti’s Monna Innominata are quite consistent across all 14 sonnets, but there is significant variation in the end-rhyme patterns of the sestet ...
1-1-patterns-inductive-reasoning-2
... Ex. 5: Examining an Unproven Conjecture • Conjecture: Every even number greater than 2 can be written as the sum of two primes. • This is called Goldbach’s Conjecture. No one has ever proven this conjecture is true or found a counterexample to show that it is false. As of the writing of this text, ...
... Ex. 5: Examining an Unproven Conjecture • Conjecture: Every even number greater than 2 can be written as the sum of two primes. • This is called Goldbach’s Conjecture. No one has ever proven this conjecture is true or found a counterexample to show that it is false. As of the writing of this text, ...
Patterns and Inductive Reasoning
... Geometry, like much of mathematics and science, developed when people began recognizing and describing patterns. In this course, you will study many amazing patterns that were discovered by people throughout history and all around the world. You will also learn to recognize and describe patterns of ...
... Geometry, like much of mathematics and science, developed when people began recognizing and describing patterns. In this course, you will study many amazing patterns that were discovered by people throughout history and all around the world. You will also learn to recognize and describe patterns of ...
Math for Poets and Drummers - SJU
... large; the challenge is to come up with a finite set of instructions—an algorithm—that generates all viable patterns. How can we check that every meter belongs somewhere in this catalog? Is there a shorthand we can use to remember a metrical pattern? Indian scholars answered these questions in ingen ...
... large; the challenge is to come up with a finite set of instructions—an algorithm—that generates all viable patterns. How can we check that every meter belongs somewhere in this catalog? Is there a shorthand we can use to remember a metrical pattern? Indian scholars answered these questions in ingen ...
Mathematics Embedded in Akan Weaving Patterns
... the world. In some cases, the designs were identical as some of the Akan ones, in other cases the similarity was almost uncanny. I found identical weaving patterns created by the people of Fiji, the Marshall Islands, the Samoans as well as the Peruvians (Inca culture). Similar to almost identical we ...
... the world. In some cases, the designs were identical as some of the Akan ones, in other cases the similarity was almost uncanny. I found identical weaving patterns created by the people of Fiji, the Marshall Islands, the Samoans as well as the Peruvians (Inca culture). Similar to almost identical we ...
Buiiding Brick Walls: Counting Techniques, Number Patterns
... This is the general case and we must be sure that our reasoning applies to ALL n bigger than 2 (we have covered the two cases for n=1 and n=2 above). Consider what happens at the left end of the wall.... ...
... This is the general case and we must be sure that our reasoning applies to ALL n bigger than 2 (we have covered the two cases for n=1 and n=2 above). Consider what happens at the left end of the wall.... ...
Fingerprint Analysis Lab
... is sufficient variability in the arrangement of minutiae to ensure that no two friction ridge patterns are identical, whether they are on different fingers of the same person or on the fingers of different people. (The same principle covers all friction ridge skin.) While this principle is difficult ...
... is sufficient variability in the arrangement of minutiae to ensure that no two friction ridge patterns are identical, whether they are on different fingers of the same person or on the fingers of different people. (The same principle covers all friction ridge skin.) While this principle is difficult ...
UnderstandPatterns Lesson 7
... • Tell students that they will have time to work individually on the rest of the Explore It problems on this page and then share their responses in groups. • As students work individually, circulate among them. This is an opportunity to assess student understanding and address student misconceptions ...
... • Tell students that they will have time to work individually on the rest of the Explore It problems on this page and then share their responses in groups. • As students work individually, circulate among them. This is an opportunity to assess student understanding and address student misconceptions ...
Inductive Reasoning
... To show that a conjecture is always true, you must prove it. To show that a conjecture is false, you have to find only one example in which the conjecture is not true. This case is called a counterexample. A counterexample can be a drawing, a statement, or a number. ...
... To show that a conjecture is always true, you must prove it. To show that a conjecture is false, you have to find only one example in which the conjecture is not true. This case is called a counterexample. A counterexample can be a drawing, a statement, or a number. ...
Document
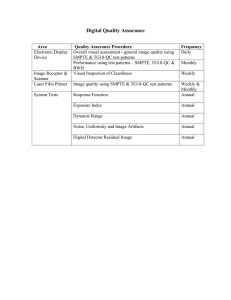
... i) the 5% patch must be just visible inside of the 0% patch, ii) the 95% patch must be just visible inside the 100% patch, iii) the optical density of various patches (for example 0%, 10%, 40% and 90%) must be within acceptable limits from the established baseline values, for the particular film use ...
... i) the 5% patch must be just visible inside of the 0% patch, ii) the 95% patch must be just visible inside the 100% patch, iii) the optical density of various patches (for example 0%, 10%, 40% and 90%) must be within acceptable limits from the established baseline values, for the particular film use ...
Moiré pattern
In mathematics, physics, and art, a moiré pattern (/mwɑrˈeɪ/; French: [mwaˈʁe]) is a secondary and visually evident superimposed pattern created, for example, when two identical (usually transparent) patterns on a flat or curved surface (such as closely spaced straight lines drawn radiating from a point or taking the form of a grid) are overlaid while displaced or rotated a small amount from one another.