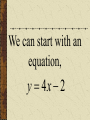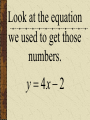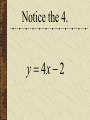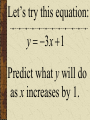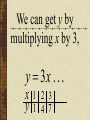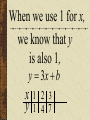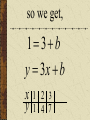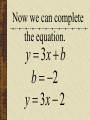* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Arithmetic and Geometric Sequence Instructional PowerPoint
History of logarithms wikipedia , lookup
Georg Cantor's first set theory article wikipedia , lookup
Location arithmetic wikipedia , lookup
Large numbers wikipedia , lookup
Patterns in nature wikipedia , lookup
Collatz conjecture wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Moiré pattern wikipedia , lookup
Patterns and Sequences Patterns and Sequences Patterns refer to usual types of procedures or rules that can be followed. Patterns are useful to predict what came before or what might come after a set a numbers that are arranged in a particular order. This arrangement of numbers is called a sequence. For example: 3,6,9,12 and 15 are numbers that form a pattern called a sequence The numbers that are in the sequence are called terms. Patterns and Sequences Arithmetic sequence (arithmetic progression) – A sequence of numbers in which the difference between any two consecutive numbers or expressions is the same. Geometric sequence – A sequence of numbers in which each term is formed by multiplying the previous term by the same number or expression. Arithmetic Sequence Find the next three numbers or terms in each pattern. a. 7, 12, 17, 22,... a. 7, 12, 17, 22,... 5 5 5 Look for a pattern: usually a procedure or rule that uses the same number or expression each time to find the next term. The pattern is to add 5 to each term. The next three terms are: 22 5 27 27 5 32 32 5 37 a. 7, 12, 17, 22,... 27,32,37 Arithmetic Sequence Find the next three numbers or terms in each pattern. b. 45, 42, 39, 36,... b. 45, 42, 39, 36,... (3) (3) (3) Look for a pattern: usually a procedure or rule that uses the same number or expression each time to find the next term. The pattern is to add the integer (-3) to each term. The next three terms are: b. 45, 42, 39, 36,... 36 (3) 33 33 (3) 30 30 (3) 27 33,30,27 Geometric Sequence Find the next three numbers or terms in each pattern. b. 3, 9, 27, 81,... b. 3, 9, 27, 81,... 3 3 3 Look for a pattern: usually a procedure or rule that uses the same number or expression each time to find the next term. The pattern is to multiply 3 to each term. The next three terms are: b. 45, 42, 39, 36,... 81 1 2 3 243 243 3 729 729 3 2187 33,30,27 Geometric Sequence Find the next three numbers or terms in each pattern. b. 528, 256, 128, 64... b. 528, 256, 128, 64,... Look for a pattern: usually a procedure or rule that uses the same number or expression each time to find the next term. The pattern is to divide by 2 to each term. The next three terms are: 64 2 32 or 64 1 64 32 1 2 2 16 2 8 or 16 1 16 8 1 2 2 1 2 or 2 2 or 1 1 2 2 or 2 Note: To divide by a number is the same as multiplying by its reciprocal. The pattern for a geometric sequence is represented as a multiplication pattern. For example: to divide by 2 is represented as the pattern multiply by ½. b. 528, 256, 128, 64,... 32 2 16 or 32 1 32 16 1 2 2 32,16,8 We can start with an equation, y 4x 2 and see what pattern develops. y 4x 2 x1 2 3 y 2 6 10 What happens to y each time x increases by 1? Remember that slope (m) = change in y change in x x1 2 3 y 2 6 10 Change in x = 1 Change in y = 4 Slope of this table is 4/1 =4 Each time x increases by 1 y increases by 4 x1 2 3 y 2 6 10 Look at the equation we used to get those numbers. y 4x 2 Notice the 4. y 4x 2 Let’s try this equation: y 3x 1 Predict what y will do as x increases by 1. y 3x 1 x y 1 2 3 ?2 ?5 ?8 There is a pattern working here. is part of the equation. 1So if w go back to the ... pattern we started with: x y 1 2 3 1 4 7 We see that y increases by 3 each time x increases by 1, and we can start writing the equation. We can get y by multiplying x by 3, y 3x . . . x y 1 2 3 1 4 7 and then adding or subtracting some number. y 3x . .b. 3x x y 1 2 3 1 4 7 When we use 1 for x, we know that y is also 1, y 3x b x y 1 2 3 1 4 7 so we get, 1 3b y 3x b x y 1 2 3 1 4 7 What does b have to be to make the equation true? 1 3b y 3x b x y 1 2 3 1 4 7 Another way to find b is to understand the table of values X 1 2 3 Y 1 4 7 The first term in the table (where x=1) shows a value of y = 1 The second term in the table (where x=2) shows a value of y = 4 The third term in the table (where x=3) shows a value of y = 7 You may recall that at the y-intercept (“b”) x = 0; therefore, the zero term in the table (where x=0) would show a value of y = -2 since the pattern (or change in y is to +3) Now we can complete the equation. y 3x b b 2 y 3x 2