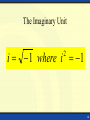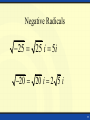* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Complex Numbers
Positional notation wikipedia , lookup
Infinitesimal wikipedia , lookup
Georg Cantor's first set theory article wikipedia , lookup
Large numbers wikipedia , lookup
Location arithmetic wikipedia , lookup
Factorization wikipedia , lookup
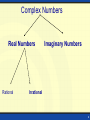
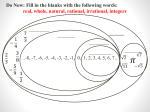
Real number wikipedia , lookup
Elementary mathematics wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Warm-up • Divide the following using Long Division: • (6x3 - 16x2 + 17x - 6) (3x –2 ) • Divide the following with Synthetic Division • (5x3 – 6x2 + 8) (x – 4) • Given the following polynomial and one of its factors, Find the remaining factors • (3x3 + 2x2 –19x + 6) : (x + 3) is a factor 1 Warm-up • Divide the following using Long Division: • (6x3 - 16x2 + 17x - 6) (3x –2 ) • 2x2 – 4x + 3 2 Warm-up • Divide the following with Synthetic Division • (5x3 – 6x2 + 8) (x – 4) 232 5 x 14 x 56 x4 2 3 Warm-up • Given the following polynomial and one of its factors, Find the remaining factors • (3x3 + 2x2 –19x + 6) : (x + 3) is a factor • (x – 2)(3x – 1) 4 Digital Lesson Complex Numbers Section 2-4 Objectives • I can use “i” to write complex numbers • I can add, subtract, and multiply complex numbers • I can simplify Negative Square Roots 6 Applications • Impedance readings for electronics and electrical circuits are all measured in complex units 7 Complex Numbers Real Numbers Rational Imaginary Numbers Irrational 8 Complex Numbers The set of all numbers that can be written in the format: a + bi ; “a” is the real number part “bi’ is the imaginary part 9 The Imaginary Unit i 1 where i 1 2 10 Negative Radicals 25 25 i 5i 20 20 i 2 5 i 11 Negative Radicals 18 32 18 4 2i 12 To add or subtract complex numbers: 1. Write each complex number in the form a + bi. 2. Add or subtract the real parts of the complex numbers. 3. Add or subtract the imaginary parts of the complex numbers. (a + bi ) + (c + di ) = (a + c) + (b + d)i (a + bi ) – (c + di ) = (a – c) + (b – d )i 13 Example: Add (11 + 5i) + (8 – 2i ) = (11 + 8) + (5i – 2i ) Group real and imaginary terms. = 19 + 3i a + bi form 14 Examples: Subtract: (– 21 + 3i ) – (7 – 9i) = (– 21 – 7) + [(3 – (– 9)]i = (– 21 – 7) + (3i + 9i) = –28 + 12i Group real and imaginary terms. a + bi form 15 The product of two complex numbers is defined as: (a + bi)(c + di ) = (ac – bd ) + (ad + bc)i 1. Use the FOIL method to find the product. 2. Replace i2 by – 1. 3. Write the answer in the form a + bi. 16 1. 7i (11– 5i) = 77i – 35i2 = 77i – 35 (– 1) = 35 + 77i 2. (2 + 3i)(6 – 7i ) = 12 – 14i + 18i – 21i2 = 12 + 4i – 21i2 = 12 + 4i – 21(–1) = 12 + 4i + 21 = 33 + 4i 17 (3 4i ) 2 (3 4i)(3 4i) 9 12i 12i 16i 2 7 24i 18 Homework • WS 3-7 19